Yong HE(何勇)Chunping ZHONG(钟春平)

1.School of Mathematical Sciences,Xiamen University,Xiamen 361005,China

2.School of Mathematical Sciences,Xinjiang Normal University,Urumqi 830053,China

ON DOUBLY WARPED PRODUCT OF COMPLEX FINSLER MANIFOLDS∗

Yong HE(何勇)1,2Chunping ZHONG(钟春平)1

1.School of Mathematical Sciences,Xiamen University,Xiamen 361005,China

2.School of Mathematical Sciences,Xinjiang Normal University,Urumqi 830053,China

E-mail:19020130154147@stu.xmu.edu.cn;zcp@xmu.edu.cn

Let(M1,F1)and(M2,F2)be two strongly pseudoconvex complex Finsler manifolds.The doubly wraped product complex Finsler manifold(f2M1×f1M2,F)of(M1,F1) and(M2,F2)is the product manifold M1×M2endowed with the warped product complex Finsler metric F2=f22F21+f21F22,where f1and f2are positive smooth functions on M1and M2,respectively.In this paper,the most often used complex Finsler connections,holomorphic curvature,Ricci scalar curvature,and real geodesics of the DWP-complex Finsler manifold are derived in terms of the corresponding objects of its components.Necessary and sufcient conditions for the DWP-complex Finsler manifold to be K¨ahler Finsler(resp.,weakly K¨ahler Finsler,complex Berwald,weakly complex Berwald,complex Landsberg)manifold are obtained,respectively.It is proved that if(M1,F1)and(M2,F2)are projectively fat,then the DWP-complex Finsler manifold is projectively fat if and only if f1and f2are positive constants.

doubly warped products;complex Finsler metric;holomorphic curvature; geodesic

2010 MR Subject Classifcation53C60;53C40

1 Introduction

Singly warped product or simply warped product of Riemannian manifolds was frst defned by O’Neill and Bishop in[12]to construct Riemannian manifolds with negative sectional curvature,then in[22],O’Neill obtained the curvature formulae of warped products in terms of curvatures of its components.The recent studies showed that warped product is useful in theoretical physics,particulary in general relativity.For instance,Beem,Ehrlich and Powell [11]pointed out that many exact solutions to Einstein’s feld equation can be expressed in terms of Lorentzian warped products.Under the assumption that four-dimensional space-time to be a general warped product of two surfaces,Katanaev,Kl¨osch and Kummer[16]explicitly constructed all global vacuum solutions to the four-dimensional Einstein equations.Doubly warped product of Riemannian manifolds was also of interesting and was studied by Unal[30].

The notion of warped product was recently extended to Finsler spaces.In[6,7],Asanov obtained some models of relativity theory which were described by the warped product of Finsler metrics.In[18],Kozma,Peter and Varga studied the warped product of real Finsler manifolds. They obtained the relationship between the Cartan connection of the warped product Finsler metric and the Cartan connections of its components.More recently,Hushmandi and Rezaii [8]studied the warped product Finsler spaces of Landsberg type,and then in[9],Hushmandi, Rezaii and Morteza obtained the curvature of warped product Finsler spaces and the Laplacian of the Sasaki-Finsler metrics.In[23],Peyghan and Tayebi obtained the relationship between the Riemannian curvature of the doubly warped product Finsler manifold and the curvatures of its components.

Let(M1,F1)and(M2,F2)be two complex Finsler manifolds.In[33],Wu and Zhong considered the product complex manifold M=M1×M2endowed with a complex Finsler metric F=f(K,H),where f(K,H)is a function of K=F21and H=F22.The possibility of F to be K¨ahler Finsler metric and complex Berwald metric were investigated.Recently in[35],Zhong showed that there are lots of strongly pseudoconvex(even strongly convex)unitary invariant complex Finsler metrics in domains in Cn.In this paper,we consider the warped product of strongly pseudoconvex complex Finsler manifolds.Our purpose of doing this is to study the possibility of constructing some special strongly pseudoconvex complex Finsler metrics such as K¨ahler Finsler metrics,weakly K¨ahler Finsler metrics,complex Berwald metrics,complex Landsberg metrics and weakly complex Berwald metrics,among which to fnd possible way to obtain strongly pseudoconvex complex Finsler metrics which are of constant holomorphic curvatures.Note that it was prove in[33]that the Chern-Finsler nonlinear connection coefcients are independent of the choice of f,i.e.,there is no diference between the case F2=f(K,H) and F2=F21+F22.In this paper,the warping product metric F on the product complex manifold M=M1×M2is F2=f22F21+f21F22,which generalizes[33]whenever f1and f2are not positive constants.

This paper is organized as follows.In Section 2,we recall some basic concepts and notions in complex Finsler geometry.In Section 3,we derive the most often used complex Finsler connections(the Chern-Finsler connection,the complex Rund connection,the complex Berwald connection,and the complex Hashiguchi connection,etc.)of the DWP-complex Finsler manifold in terms of the corresponding connections of its components,respectively.In Section 4,we derive the formulae of the holomorphic curvature and Ricci scalar curvature of the DWP-complex Finsler manifold in terms of the holomorphic curvatures and Ricci scalar curvatures of its components.In Section 5,we obtain the necessary and sufcient conditions for the DWP-complex Finsler manifold to be K¨ahler Finsler(resp.weakly K¨ahler Finsler,complex Berwald,weakly complex Berwald,complex Landsberg,complex locally Minkowski)manifold. In Section 6,we derive the real geodesic equations of the DWP-complex Finsler manifold in terms of the geodesic equations of its components,and prove that if the warping function f1(resp.f2)is a positive constant,then(M1,F1)(resp.(M2,F2))is a totally geodesic manifold of the DWP-complex Finsler manifold(f2M1×f1M2,F),and the projection of any geodesic of the DWP-complex Finsler manifold onto M1(resp.M2)is a geodesic of(M1,F1)(resp.(M2,F2)). In Section 7,we prove that if(M1,F1)and(M2,F2)are locally projectively fat manifolds,then the DWP-complex Finsler manifold(f2M1×f1M2,F)is projectively fat if and only if f1andf2are positive constants.

The main results in this paper are as follows.

Theorem 1.1Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1) and(M2,F2).Then the holomorphic curvature of(M,F)along a holomorphic tangent vector v=(vi,vi′)∈T1,0zM satisfying F1(π1(v))=1 and F2(π2(v))=1 is given by

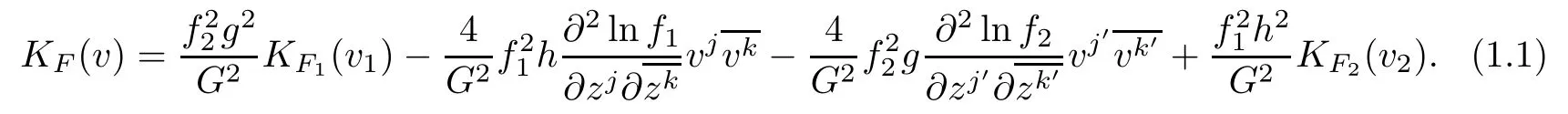
Theorem 1.1 implies that if KF1(π1(v))=KF2(π2(v))≡c,then KF(v)≡c if and only if the warping functions lnf1and lnf2are pluriharmonic functions on M1and M2,respectively.

Theorem 1.2Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1)and (M2,F2).Then the Ricci scalar curvature of(f2M1×f1M2,F)associated to the Chern-Finsler connections is given by

where RicF1and RicF2are Ricci scalar curvature of(M1,F1)and(M2,F2),respectively.

Theorem 1.2 implies that equality(1.2)is independent of the choice of the warping functions f1and f2.

Theorem 1.3Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of two weakly K¨ahler Finsler manifolds(M1,F1)and(M2,F2).Then(f2M1×f1M2,F)is a weakly K¨ahler Finsler manifold if and only if the functions f1and f2are positive constants.

Theorem 1.4The DWP-complex Finsler manifold(f2M1×f1M2,F)is a complex Berwald manifold if and only if(M1,F1)and(M2,F2)are complex Berwald manifolds and the functions f1and f2are positive constants.

Theorems 1.3 and 1.4 imply that unless the doubly warping function f1and f2are positive constants,the doubly warped product operation does not preserve weakly K¨ahler Finsler manifolds and complex Berwald manifolds.

Theorem 1.5The DWP-complex Finsler manifold(f2M1×f1M2,F)is a weakly complex Berwald manifold if and only if(M1,F1)and(M2,F2)are weakly complex Berwald manifolds.

Theorem 1.5 implies that the doubly warped product operation preserves weakly complex Berwald metrics.Since there are lots of weakly complex Berwald metrics(see[35]),this theorem provides us an efective way to construct new weakly complex Berwald metrics.

Theorem 1.6Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of two complex Finsler manifolds(M1,F1)and(M2,F2).

(i)If the warping functions f1(resp.f2)is a positive constant on M1(resp.M2),then any geodesic of(M1,F1)(resp.(M2,F2))is a geodesic of(f2M1×f1M2,F),that is to say(M1,F1) (resp.(M2,F2))is a totally geodesic subspace of the doubly warped product complex Finsler space(f2M1×f1M2,F).

(ii)If the warping functions f1(resp.f2)is a positive constant on M1(resp.M2),then the projection of any geodesic of the DWP-complex Finsler manifold(f2M1×f1M2,F)onto M1(resp.M2)is a geodesic of(M1,F1)(resp.(M2,F2)).

Theorem 1.7Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of two strongly convex complex Finsler manifolds(M1,F1)and(M2,F2).

(i)If(M1,F1)and(M2,F2)are locally projectively fat manifolds,then(f2M1×f1M2,F) is a locally projectively fat manifold if and only if the warping functions f1and f2are positive constants.

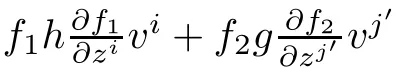
2 Preliminary

Let M be a complex manifold of complex dimension n.We denote z=(z1,···,zn)the local holomorphic coordinates on M,and(z,v)=(z1,···,zn,v1,···,vn)the induced local holomorphic coordinates on the holomorphic tangent bundle T1,0M of M.We shall assume that M is endowed with a strongly pseudoconvex complex Finsler metric F in the following sense.

Defnition 2.1(see[1]) A strongly pseudoconvex complex Finsler metric F on a complex manifold M is a continuous function F:T1,0M→R+satisfying

(i)G=F2is smooth on˜M=T1,0M−{zero section};

(ii)F(p,v)>0 for all(p,v)∈ ˜M;

(iii)F(p,ζv)=|ζ|F(p,v)for all(p,v)∈T1,0M and ζ∈C;

(iv)the Levi matrix(or complex Hessian matrix)

is positive defnite on˜M.

In this paper,we denote(Gνβ)the inverse matrix of(Gαν)such that GνβGαν=δβα.We also use the notion in[1],that is,the derivatives of G with respect to the v-coordinates and z-coordinates are separated by semicolon;for instance,

Let(M1,F1)and(M2,F2)be two strongly pseudoconvex complex Finsler manifolds with dimCM1=m and dimCM2=n,then M=M1×M2is a strongly pseudoconvex complex Finsler manifold with dimCM=m+n.

Throughout this paper we use the natural product coordinate system on the product manifold M=M1×M2.Let(p0,q0)be a point in M,then there are coordinate chart(U,z1) and(V,z2)on M1and M2,respectively,such that p0∈U and q0∈V.Thus we obtain a coordinate chart(W,z)on M such that W=U×V and(p0,q0)∈W,and for all(p,q)∈W, z(p,q)=(z1(p),z2(q)),where π1:M1×M2→M1,π2:M1×M2→M2are natural projections.

Let T1,0M1,T1,0M2and T1,0M be the holomorphic tangent bundles of M1,M2and M, respectively.Denote dπ1:T1,0(M1×M2)→ T1,0M1,dπ2:T1,0(M1×M2)→ T1,0M2the holomorphic tangent maps induced by π1and π2,respectively.Note that dπ1(z,v)=(z1,v1) and dπ2(z,v)=(z2,v2)for every v=(v1,v2)∈T1,0z(M1×M2)with v1=(v1,···,vm)∈T1,0z1M1and v2=(vm+1,···,vm+n)∈T1,0z2M2.Denote˜M1=T1,0M1−{zero section},˜M2=T1,0M2−{zero section},fM=fM1×fM2⊂T1,0(M1×M2)−{zero section}.

Defnition 2.2Let(M1,F1)and(M2,F2)be two strongly pseudoconvex complex Finsler manifolds and f1:M1→(0,+∞)and f2:M2→(0,+∞)be smooth functions.The doubly warped product(abbreviated as DWP)complex Finsler manifold of(M1,F1)and(M2,F2) is the product complex manifold M=M1×M2endowed with the complex Finsler metricgiven by

for z=(z1,z2)∈M and v=(v1,v2)∈T1,0zM−{zero section}.The functions f1and f2are called warped functions.The DWP-complex Finsler manifold of(M1,F1)and(M2,F2)is denoted by(f2M1×f1M2,F).

It is obvious that the function F defned by(2.2)is a strongly pseudoconvex complex Finsler metric on M.Note that it is natural to ask F to be defned onfM rather than on T1,0(M1×M2)−{zero section},or onfM1×T1,0M2,or on T1,0M1×fM2,since Fiis smooth on T1,0Miif and only if Ficomes from a Hermitian metric on Mifor i=1,2.

If either f1=1 or f2=1,but not both of them,then(f2M1×f1M2,F)becomes a warped product of complex Finsler manifolds(M1,F1)and(M2,F2).If f1≡1 and f2≡1,then (f2M1×f1M2,F)becomes a product of complex Finsler manifolds(M1,F1)and(M2,F2).If neither f1nor f2is a constant,then we call(f2M1×f1M2,F)a nontrivial(proper)DWP-complex Finsler manifold of(M1,F1)and(M2,F2).

The local coordinates(z,v)onfM are transformed by the rules

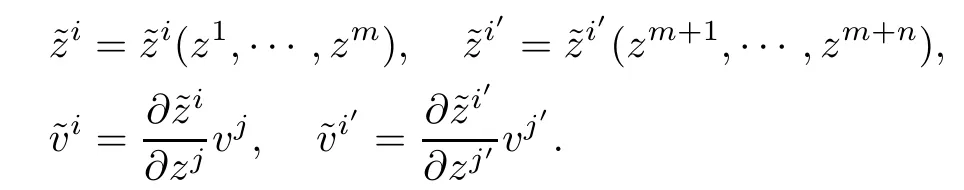
For∂/∂vα,we have

Denote g=F21,h=F22,so that G=F2=f22g+f21h and

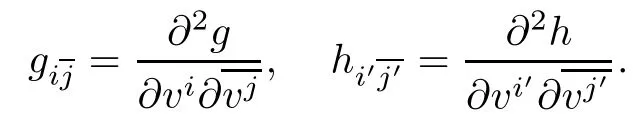
The fundamental tensor matrix of F is given by

with its inverse matrix(Gβα)given by

Let V1,0be the holomorphic vertical vector subbundle ofwhich is locally spanned by the nature frame feldsand is called the doubly warped vertical distribution onThen,the complementary vector subbundleis locally spanned bywhereis called the doubly warped horizontal distribution onfM.Thus the holomorphic tangent bundleadmits the decomposition

3 Connections of DWP-complex Finsler Manifold

In complex Finsler geometry,the Chern-Finsler connection is the most often used complex Finsler connection.There are also other complex Finsler connections,such as complex Rund connection,complex Berwald connection,complex Hashiguchi connection and Rund type complex Finsler connection used in various topics[27].

In this section we derive these connections of DWP-complex Finsler manifold,which are expressed in terms of connections of its components.

The Chern-Finsler complex nonlinear connectionassociate to a given strongly pseudoconvex complex Finsler metric F is given by

The Chern-Finsler connection D:X(V1,0)→ X(T∗CfM ⊗V1,0)associated to a strongly pseudoconvex complex Finsler metric F was frst introduced in[17]and systemically studied in[1].Essentially,the Chern-Finsler connection associated to F is the Hermitian connection on the holomorphic vector bundle V1,0endowed with the Hermitian metric h·,·i induced by F. The connection 1-forms ωαβof D is of type(1,0)and are given by

where

and

In the following we denote

Note that

Lemma 3.1Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1)and (M2,F2).Then the Chern-Finsler complex nonlinear connection coefcients associated to F are given by

where

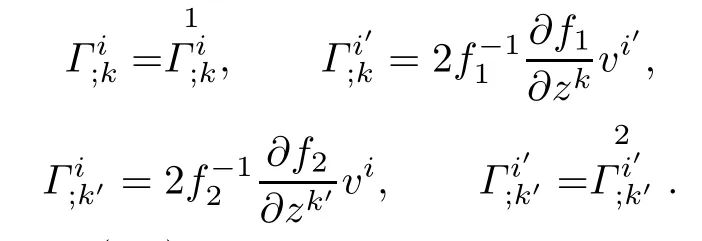
ProofBy using(2.5)and(3.1),we have

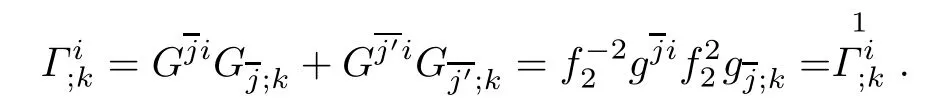
Similarly,we can obtain other equalities in Lemma 3.1.

Using(3.3),(3.4)and Lemma 3.1,after a straightfoward computation,we have

Proposition 3.2Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1) and(M2,F2),Γαβ;µand Γαβµare the horizontal and vertical coefcients of the Chern-Finsler connection associated to F,respectively.Then

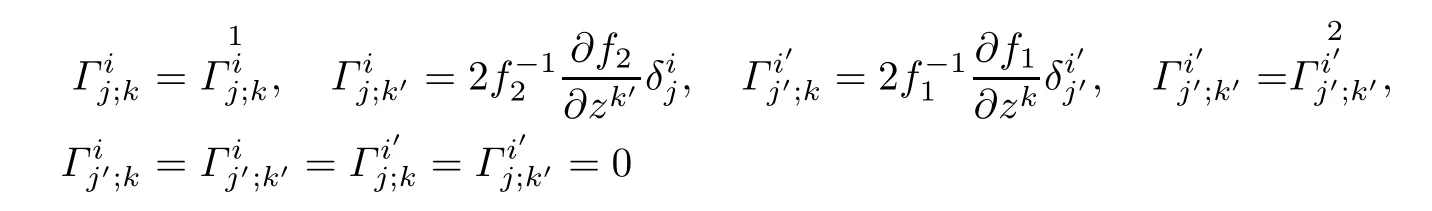
and

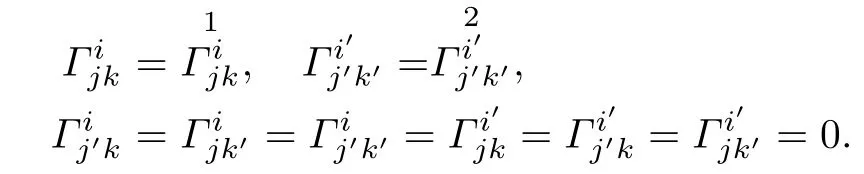
Using(3.3)and Lemma 3.1,we have

Proposition 3.3Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1) and(M2,F2),Γαβ;µbe the coefcients of the complex Rund connection associated to F.Then

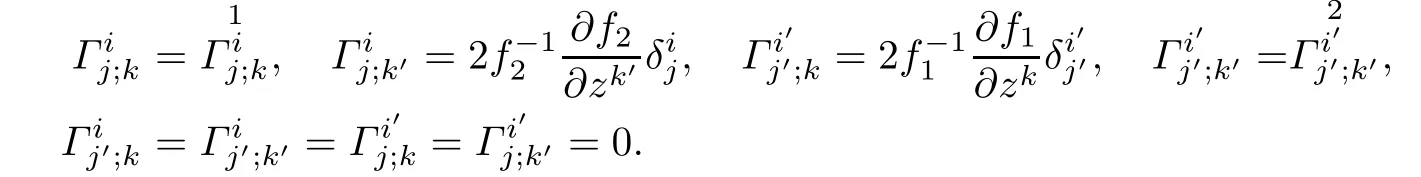
Next we shall derive the complex Berwald nonlinear connection coefcientswhich is obtained fromAccording to[21],the complex nonlinear connectionalways determine a complex sprayConversely,the complex spray Gαinduces another complex nonlinear connection denoted by

which are called the complex Berwald nonlinear coefcients associated to F.Note that we always have

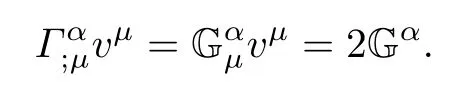
The complex Berwald connectionwas frst introduced in [21],and its connection 1-form can be expressed as

where

By Lemma 3.1 one may easily establish the following result.

Lemma 3.4Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1)and (M2,F2).Then the complex spray coefcients Gαassociated to Γα;µ(or equivalently Gαµ)are given by

Using(3.8),(3.10)and Lemma 3.4,by a straight forward computation,we obtain the following result.

Lemma 3.5Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1)and (M2,F2).Then the complex Berwald nonlinear connection coefcients Gαµare given by

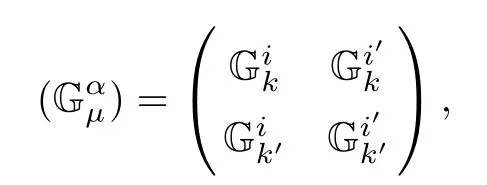
where

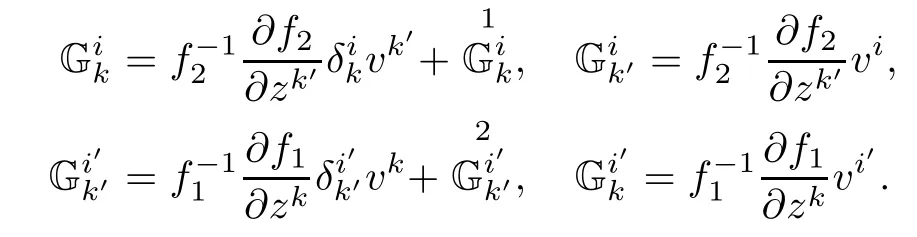
Corollary 3.6Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1) and(M2,F2).Then the complex Berwald connection coefcients Gαβµassociated to F are given by

The complex Hashiguchi connectionis a complex analogue of the Hashiguchi connection in real Finsler geometry[19].Its connection 1-formsare given by

where Gαβµare given by(3.10),Γαβµare given by(3.4)and

Proposition 3.7Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1) and(M2,F2).Then the horizontal and vertical connection coefcients of the complex Hashiguchi connection,respectively Gαβµand Γαβµare given by Proposition 3.3 and Corollary 3.6.

In[5],Aldea and Munteanu gave the defnition of complex Landsberg space.A complex Finsler manifold(M,F)is called a complex Landsberg manifold if

where

Proposition 3.8Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1) and(M2,F2).Then

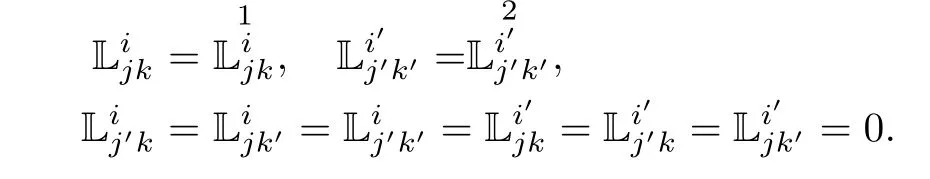
ProofUsing(2.4),(2.5),(3.13),(3.14)and Lemma 3.5,we have

Similarly,we can obtain other equalities of Proposition 3.8.

4 Holomorphic Curvature and Ricci Scalar Curvature of Doubly Warped Product Complex Finsler Manifold

Our purpose in this section is to derive formulae of the holomorphic curvature and Ricci scalar curvature of DWP-complex Finsler manifold in terms of the holomorphic curvature and Ricci scalar curvature of its components.

In a complex Finsler space(M,F),there are two ways of defning the holomorphic curvature of F.

The frst method gives the holomorphic curvature on(M,F)from the Gauss curvature on the unit disc△ ⊂C via a holomorphic map ϕ:△ → M.More precisely,the holomorphic curvature is defned by KF(v)=sup{K(ϕ∗G)(0)}[31].The second method to defne the holomorphic curvature on(M,F)from the curvature tensor Ω of a complex Finsler connection and this was considered by Kobayashi[17],and locally expression of the holomorphic curvature of a strongly pseudoconvex Finsler metric F alongwith respect to Chern-Finsler connection D is given by Abate and Patrizio[1]:

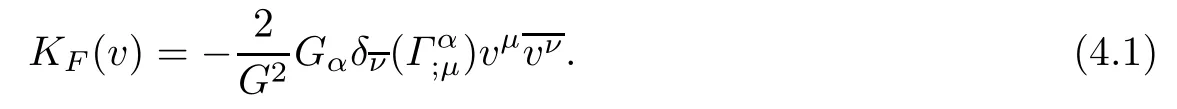
In[3],Aikou proved that the above two defnitions is equivalent to each other,and if F comes from a Hermitian metric on M,then the holomorphic curvature is just the holomorphic sectional curvature in the usual sense[32].

In[27],Sun and Zhong pointed out that the holomorphic curvature of a strongly pseudoconvex Finsler metric F along a nonzero vectorwith respect to the Chern-Finsler connection D,or the complex Rund connectionˆD,or the complex Berwald connection˘D,or the complex Hashiguchi connectionˇD,are coincide with each other.In the following,we use the Chern-Finsler connection to derive the holomorphic curvature of the DWP-complex Finsler manifold.

Theorem 4.1Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1) and(M2,F2).Then the holomorphic curvature of(M,F)along a holomorphic tangent vectorsatisfying F1(π1(v))=1 and F2(π2(v))=1 is given by

ProofThe holomorphic curvature of the DWP-complex Finsler manifold(f2M1×f1M2, F)with respect to the Chern-Finsler connection is given by

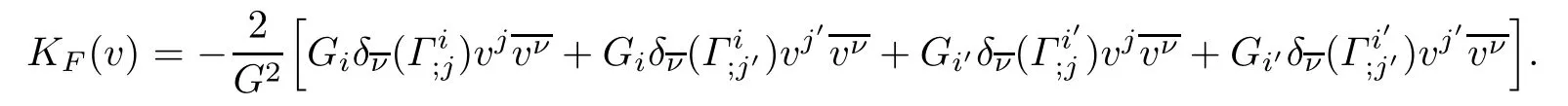
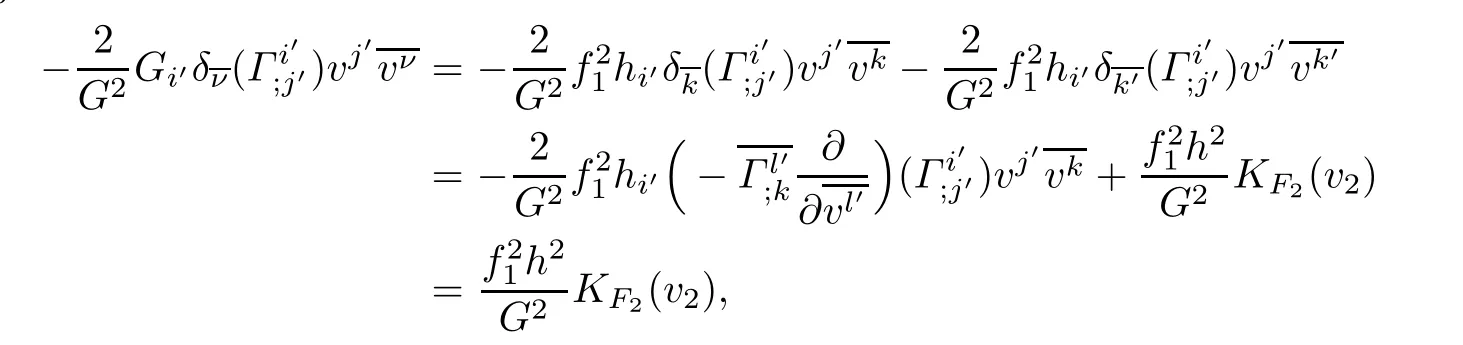
where in the last equality we used

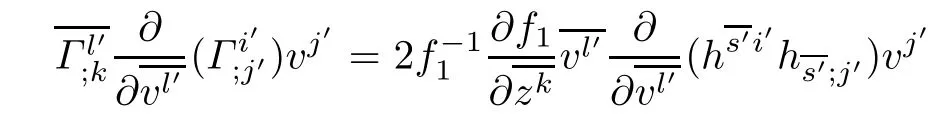
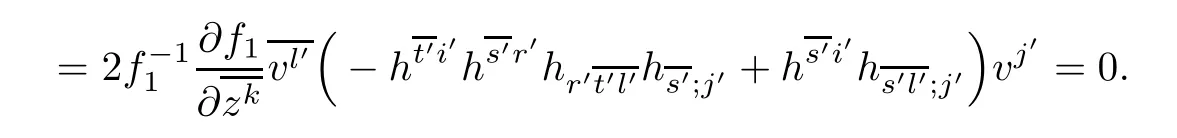
Similarly,we have

Thus we get(4.2).

Corollary 4.2Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1) and(M2,F2).If KF1(π1(v))=KF2(π2(v))≡c,lnf1and lnf2are pluriharmonic functions on M1and M2,respectively.Then the holomorphic sectional curvature of(f2M1×f1M2,F)along v=(vi,vi′)is

The Ricci scalar curvature of F along a nonzero vectorassociated to the Chern-Finsler connection is given by[21]:

Theorem 4.3Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1)and (M2,F2).Then the Ricci scalar curvature of(f2M1×f1M2,F)associated to the Chern-Finsler connection is given by

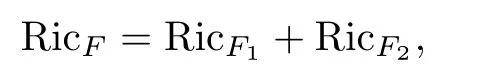
where RicF1and RicF2are Ricci scalar curvatures of(M1,F1)and(M2,F2),respectively.

ProofUsing(4.4),we have

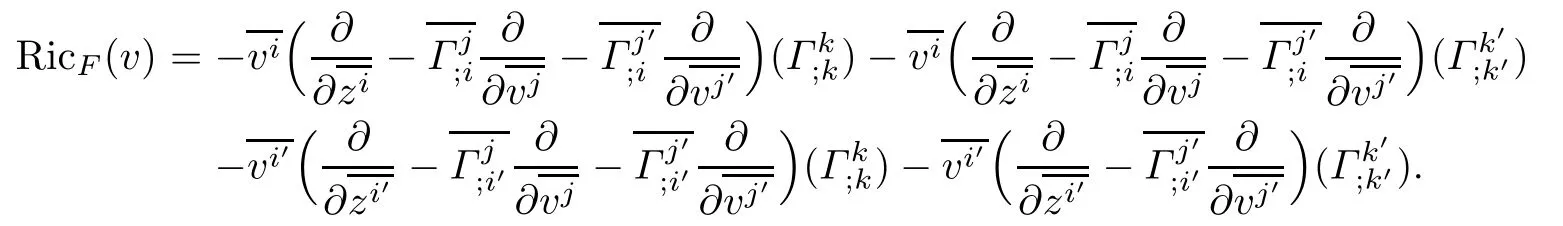
Using Lemma 3.1,and notice thatit follows that

Similar calculations gives

Thus

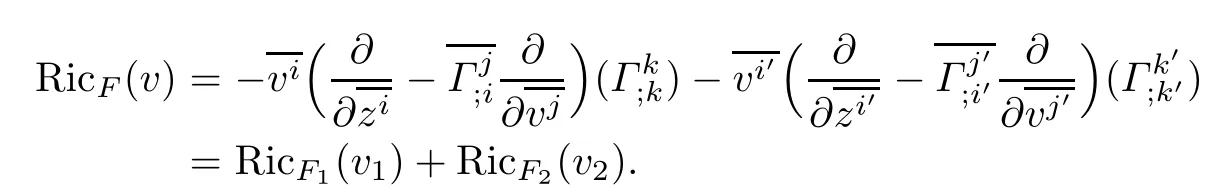
5 Doubly Warped Product of Special Complex Finsler Manifolds

Let(M1,F1)and(M2,F2)be two K¨ahler Finsler(or weakly K¨ahler Finsler,complex Berwald,weakly complex Berwald,complex Landsberg)manifold,one may want to know whether the DWP-complex Finsler manifold(f2M1×f1M2,F)is also a K¨ahler Finsler(or weakly K¨ahler Finsler,complex Berwald,weakly complex Berwald,complex Landsberg)manifold.In this section,we shall give a complete answer to these questions.

Defnition 5.1(see[1]) Let F be a strongly pseudoconvex complex Finsler metric on a complex manifold M.F is called a strongly K¨ahler Finsler metric ifcalled a K¨ahler Finsler metric ifcalled a weakly K¨ahler Finsler metric if

In[13],Chen and Shen proved that a K¨ahler Finsler metric is actually a strongly K¨ahler Finsler metric.Thus there are only two K¨ahlerian notions in Finsler setting,i.e.,K¨ahler Finsler metric and weakly K¨ahler Finsler metric.

Now,let us consider the case of K¨ahler Finsler manifolds and weakly K¨ahler Finsler manifolds.We have the following theorem.

Theorem 5.2Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1) and(M2,F2).Then(f2M1×f1M2,F)is a K¨ahler Finsler manifold if and only if(M1,F1)and (M2,F2)are K¨ahler Finsler manifolds and the functions f1and f2are positive constants.

ProofAssume that(f2M1×f1M2,F)is a K¨ahler Finsler manifold,then Γαβ;µ=Γαµ;β.By Proposition 3.2,this is equivalent to

Thus(M1,F1)and(M2,F2)are K¨ahler Finsler manifolds and the functions f1and f2are positive constant.

Theorem 5.3Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of two weakly K¨ahler Finsler manifolds(M1,F1)and(M2,F2).Then(f2M1×f1M2,F)is a weakly K¨ahler Finsler manifold if and only the functions f1and f2are positive constants.

ProofBy puttingµ=k in(5.1)and using Proposition 3.2,after a long but trivial computation,we obtain

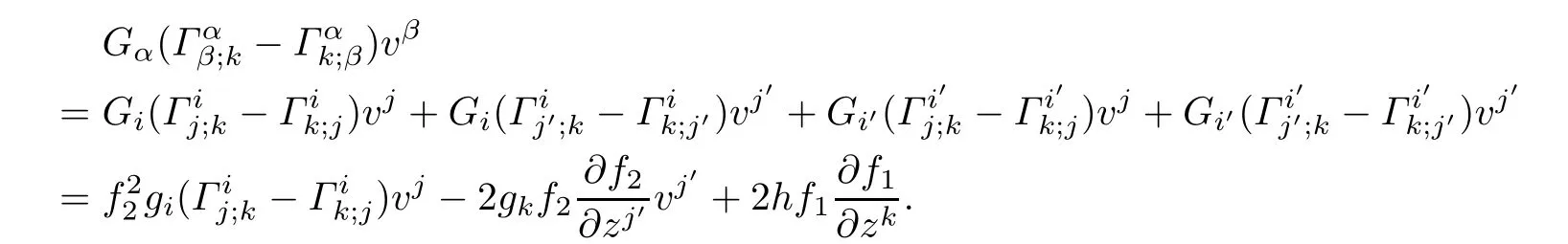
Similary,By puttingµ=k′in(5.1),we obtain

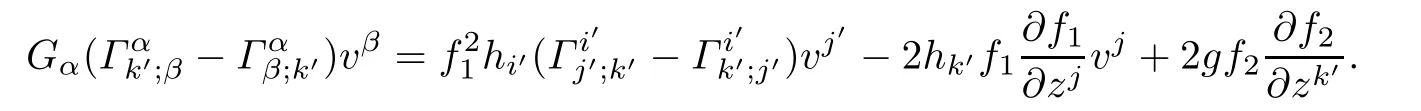
By Defnition 5.1,(f2M1×f1M2,F)is a weakly K¨ahler Finsler manifold if and only if

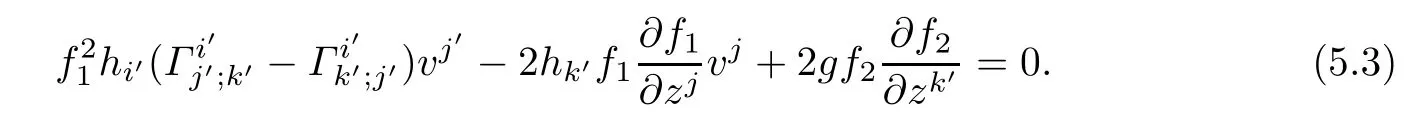
Note that gi(Γij;k−Γik;j)vjand f1are independent of vk′,thus diferentiating(5.2)with respect to vk′,we get

Interchanging indices j and k in(5.2),and then contracting the obtained equality with vj,we get

Contracting(5.3)with vk′,we get

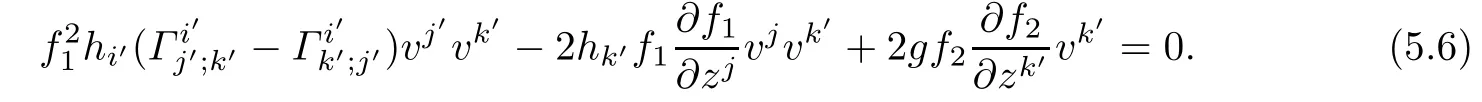
Now subtracting(5.6)from(5.5)and using(5.4),we get

Since(M1,F1)and(M2,F2)are weakly K¨ahler Finsler manifolds,we have

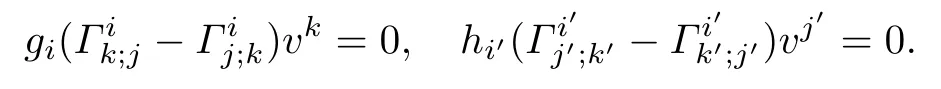
Thus we obtain the following diferential equation

Note that the left hand side of(5.8)depends only on(z1,v1),while the right hand side of(5.8) depends only on(z2,v2),thus we get

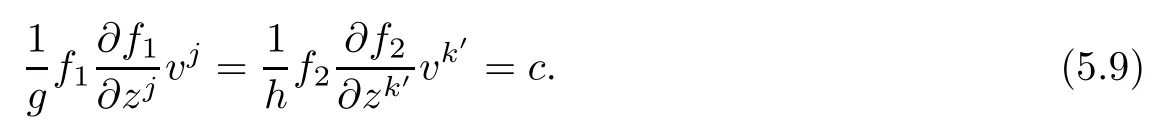
Suppose c 6=0,then

Diferentiating the above two equations with respect to vi,vjand vi′,vj′,respectively,we get

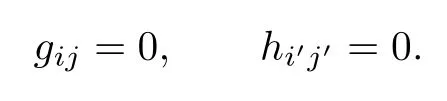
This is a contradiction since(gij)and(hi′j′)are positive defnite matrices.Thus it necessary that c=0,which implies that f1and f2are positive constants.

As an immediate consequence of relations(2.4),we have

Theorem 5.4The DWP-complex Finsler manifold(f2M1×f1M2,F)is a Hermitian manifold if and only if(M1,F1)and(M2,F2)are Hermitian manifolds.

For the case of complex Berwald manifold,weakly complex Berwald manifold and complex Landsberg manifolds,we need the following defnitions.

Defnition 5.5(see[4]) A complex Finsler manifold(M,F)is called a complex Berwald manifold if the horizontal connection coefcients Γαβ;µ(z,v)of the Chern-Finsler connection are independent of fbre coordinates v and its associated Hermitian metric hFis a K¨ahler metric on M.

Remark 5.6In[2],Aikou gave the defnition of complex Berwald manifold in which there is no requirement of the K¨ahler Finsler condition.But diferent from real Finsler geometry, in complex Finsler geometry,there exists two diferent covariant derivative for Cartan tensor, Cijk|hand Cijk|h.The requirement of the K¨ahler Finsler condition in[4]implies that Cijk|h=0. Later the above defnition of complex Berwald manifold was given by Aikou himself[4],and was widely used in various topics[3,5].In this paper,complex Berwald manifold is in the sense of Aikou[4].

Defnition 5.7(see[34]) Let F be a strongly pseudoconvex complex Finsler metric on M. If locally the connection coefcients Gαβµ(z,v)of the associated complex Berwald connection are independent of fbre coordinates v,then F is called a weakly complex Berwald metric.

Defnition 5.8(see[5]) Let F be a complex Finsler metric on complex manifold M.F is said to be a complex Landsberg metric if it satisfes

Theorem 5.9The DWP-complex Finsler manifold(f2M1×f1M2,F)is a complex Berwald manifold if and only if(M1,F1)and(M2,F2)are complex Berwald manifolds and the functions f1and f2are positive constants.

ProofAccording to Theorem 5.2 and Defnition 5.5,(f2M1×f1M2,F)is a complex Berwald manifold if and only if(M1,F1)and(M2,F2)are K¨ahler manifolds,the functions f1and f2are positive constants and Γαβ;µ(z,v)=Γαβ;µ(z).Thus by the relations of the coefcient Γαβ;µof the Chern-Finsler connection in Proposition 3.2,we have

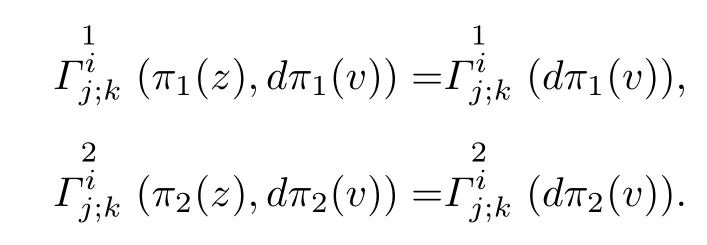
This is equivalent to the conditions that(M1,F1)and(M2,F2)are complex Berwald manifolds and the functions f1and f2are positive constants.

In the sense of Aikou[3,4],a complex Finsler manifold(M,F)is said to be modeled on a complex Minkowski space if the connection coefcients Γαβ;µ(z,v)of the Chern-Finsler connection depend only on the coordinates of the base manifoldSo, according to Proposition 3.2,we have

Corollary 5.10The DWP-complex Finsler manifold(f2M1×f1M2,F)is modeled on a complex Minkowski space if and only if(M1,F1)and(M2,F2)are modeled on a complex Minkowski spaces.

In the sense of Aikou[2],a complex Finsler manifold(M,F)is said to be complex locally Minkowski,if there exits an open coversuch that on eachthe function F is a function of the fbre-coordinate only.A complex Finsler manifold(M,F)is complex locally Minkowski if and only if it is modeled on a complex Minkowski space and the complex Rund connection(i.e.,the connection coefcients Γαβ;µ(z,v)of the associated Chern-Finsler connection)on(M,F)is holomorphic.In[4],Aikou gave an example of complex manifold which is modeled on a complex Minkowski space,but not complex locally Minkowski.

According to Proposition 3.2,we have

Corollary 5.11If lnf1and lnf2are pluriharmonic functions on M1and M2,respectively, then the DWP-complex Finsler manifold(f2M1×f1M2,F)is a complex locally Minkowski if and only if(M1,F1)and(M2,F2)are complex locally Minkowski manifolds.

Theorem 5.12The DWP-complex Finsler manifold(f2M1×f1M2,F)is a weakly complex Berwald manifold if and only if(M1,F1)and(M2,F2)are weakly complex Berwald manifolds.

ProofAccording to Defnition 5.7,(f2M1×f1M2,F)is a weakly complex Berwald manifold if and only if Gαβµ(z,v)=Gαβµ(z).Thus by the relations of the complex Berwald connection in Proposition 3.6,we have

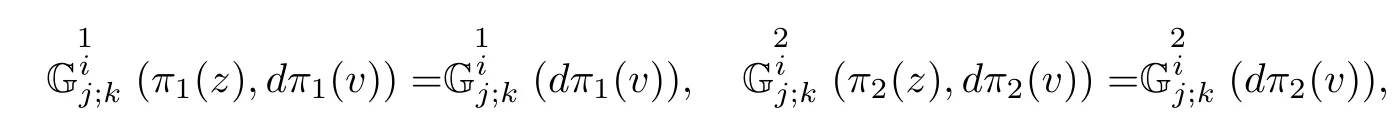
which is equivalent to the condition that(M1,F1)and(M2,F2)are weakly complex Berwald manifolds. ?

Remark 5.13It was shown in[34]that the complex Wrona metric is a weakly complex Berwald metric,but not a complex Berwald metric.This assertion was proved by showing that Gα=12Γα;µvµ≡0 while Γα;µdo not vanish identically.It was also shown in[35]that there are lots of unitary invariant strongly pseudoconvex complex Finsler metric which are weakly complex Berwald metrics.Theorem 5.12 provide us an efective way to construct weakly complex Berwald manifolds.

Theorem 5.14The DWP-complex Finsler manifold(f2M1×f1M2,F)is a complex Landsberg manifold if and only if(M1,F1)and(M2,F2)are complex Landsberg manifolds and the functions f1and f2are positive constants.

ProofAccording to Defnition 5.8,Propositions 3.6 and 3.8,(f2M1×f1M2,F)is a complex Landsberg manifold if and only if

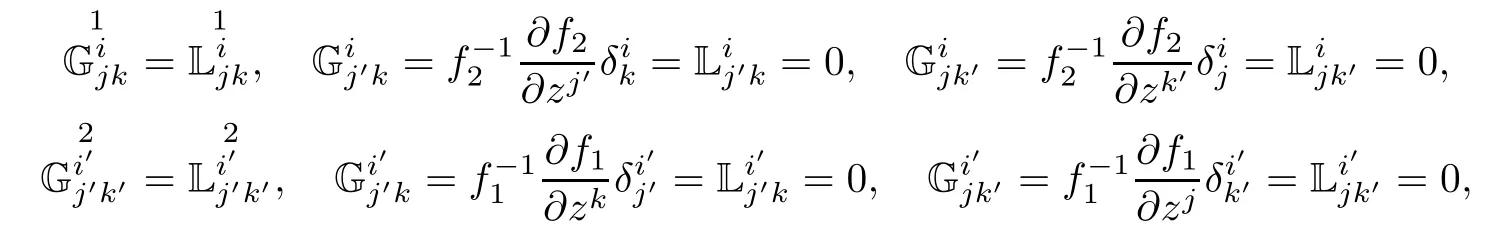
which is equivalent to the condition that(M1,F1)and(M2,F2)are complex Landsberg manifolds and the functions f1and f2are positive constants.

A complex n-dimensional complex Finsler space(M,F)is called a G-Landsberg spaces if it is complex Landsberg and the spray coefcient Gαare holomorphic with respect to v,i.e., ˙∂µ(Gα)=0[5].Thus we have

Corollary 5.15The DWP-complex Finsler manifold(f2M1×f1M2,F)is a complex GLandsberg manifold if and only if(M1,F1)and(M2,F2)are complex G-Landsberg manifolds and the functions f1and f2are positive constants.

Remark 5.16In real Finsler Geometry,every Berwald space is a Landsberg space,the converse,however,is still an open problem[10].This problem was studied by several authors [20,25,28,29].In complex Finsler geometry,there is also notions of complex Berwald metric and complex Landsberg metric.Every complex Berwald metric is complex Landsberg metric [5].One may want to know whether every complex Landsberg metric is also a complex Berwaldmetric.By Theorems 5.9 and 5.14,it follows that these two class of manifolds are the same type complex Finsler manifolds under warped product operations,thus showing that it is impossible to construct such metrics by this method.But,if we have two complex Landsberg manifolds M1and M2which are not complex Berwald manifolds,we can use the above Theorems to produce such manifolds of dimension dimCM1+dimCM2,as follows.

Let M1and M2be two complex Landsberg manifolds,but they are not complex Berwald manifolds.Now,for any positive constant functions f1:M1→R+and f2:M2→R+,Theorem 5.14 ensures that the DWP-complex Finsler manifold(f2M1×f1M2,F)is a complex Landsberg manifold.Theorem 5.9 guarantees that it is not a complex Berwald manifold,otherwise,M1and M2must be complex Berwald manifolds,which is a contradiction to the choice of M1and M2.

Practical application of this method depends on the existence of a non-Berwald complex Landsberg manifold to start with.If there is,we would prefer to select one with the lowest dimension.Let us have complex Landsberg manifolds which are not Berwald,ordered according to their dimension.Then,by well-ordering principle,there exists a natural number that is the lowest dimension of such manifolds,and there exists a manifold of this type,which has this dimension.We have the following corollary of the theorems.

Corollary 5.17Let C be the collection of complex Landsberg manifolds which are not complex Berwald manifold.Assume that C is non-empty.Let m0be the lowest dimension. Let M be a complex Finsler manifold in C with dimension m0,then M cannot be of warped product type.

ProofLet,on the contrary,M be of warped product type,that is,M=(f2M1×f1M2,F) for some functions f1:M1→ R+and f2:M2→ R+,then,by Theorem 5.14,M1and M2are complex Landsberg manifold,and according to Theorem 5.9,M1and M2are not complex Berwald manifolds,otherwise M itself should be a complex Berwald manifold.But,as dimCM1≥1,M1itself is a member of C,whose dimension should less than m0,contradicting the choice of m0.

6 Geodesics of Doubly Warped Product Complex Finsler Manifold

In this section,we shall investigate geodesics of DWP-complex Finsler manifold.

A real geodesic σα(t)with an afne parameter t of a complex Finsler manifold(M,F) satisfes the following equation[1]:

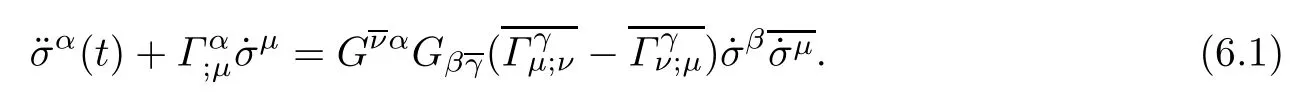
Proposition 6.1Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1) and(M2,F2).If σ(t)=(σα(t))=(σk(t),σk′(t))is a geodesic of(f2M1×f1M2,F),then it is necessary that

ProofBy putting α=k in(6.1),using(2.4),(2.5)and Proposition 3.2,after a long computation,we obtain

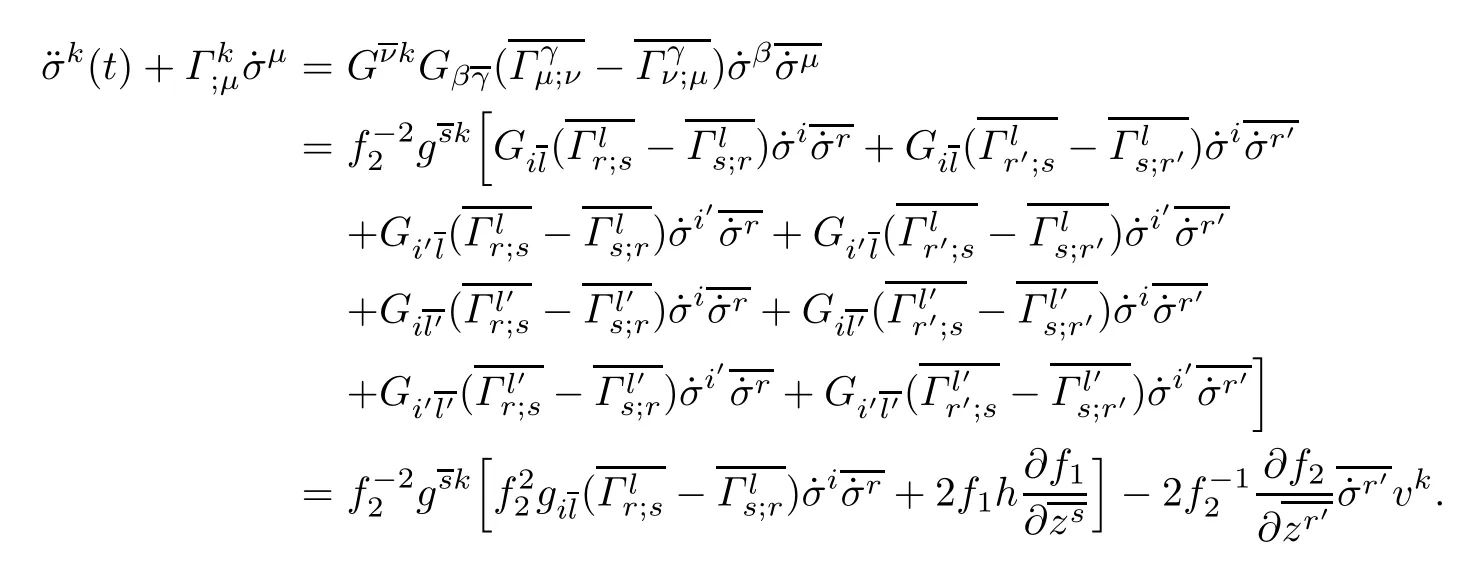
Similary,by putting α=k′in(6.1),using(2.4),(2.5)and Proposition 3.2,we obtain

which completes the proof.

Corollary 6.2Let(M1×f1M2,F)be a product complex Finsler manifold of(M1,F1) and(M2,F2).If{σk(t)}and{σk′(t)}are real geodesics of F1and F2,respectively.Then {σα(t)}={σk(t),σk′(t)}is a geodesic of F if and only if f1is a positive constant function on M1.

Theorem 6.3Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of(M1,F1)and (M2,F2).

(i)If the warping function f1(resp.f2)is a positive constant on M1(resp.M2),then any geodesic of(M1,F1)(resp.(M2,F2))is a geodesic of(f2M1×f1M2,F),that is to say,(M1,F1) (resp.(M2,F2))is a totally geodesic subspace of the doubly warped product complex Finsler space(f2M1×f1M2,F).

(ii)If the warping function f1(resp.f2)is a positive constant on M1(resp.M2),then the projection of any geodesic of the DWP-complex Finsler manifold(f2M1×f1M2,F)onto M1(resp.M2)is a geodesic of(M1,F1)(resp.(M2,F2)).

ProofSince the proof of(ii)is similar to(i),we only prove(i).If(σk(t))is a geodesic of (M1,F1),then

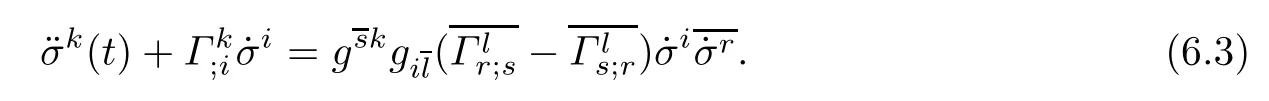
Consider the curve(σk(t),σk′),where σk′is a constant.We have˙σi′=0,thus the diferential equation(6.2)reduces to

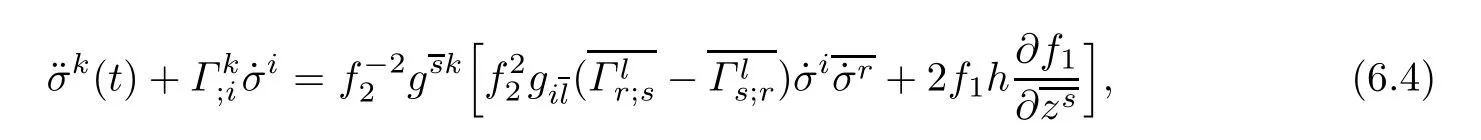
7 Projective Flatness of Doubly Warped Product Complex Finsler Manifold

Let F(x,u)be a real Finsler metric defned on a domain D⊂Rn.F is called projectively fat if its geodesic are straight lines[14].This is equivalent to the following system of PDEs[15]

where x=(x1,···,xn)∈D and u=(u1,···,un)∈TxD,F is called dually fat if and only if F satisfes[26]

For a strongly convex complex Finsler metric,it makes sense to talk about its projectiveness.

Let(M1,F1)and(M2,F2)be two locally projectively fat or dually fat Finsler manifold, one may want to know whether the DWP-complex Finsler manifold(f2M1×f1M2,F)is also a locally projectively fat or dually fat complex Finsler manifold.For this problem we need the following proposition.

Proposition 7.1(see[35]) Let F be a strongly convex complex Finsler metric defned on a domain D⊂Cn.Then

(i)F is locally projectively fat if and only if

(ii)F is locally dually fat if and only if

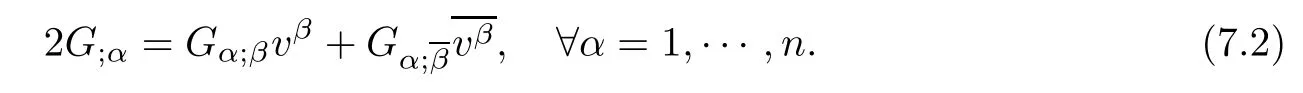
It is obviously that F is a strongly convex complex Finsler metric whenever F1and F2are strongly convex complex Finsler metrics.Thus it makes sense to investigate the projective fatness or dual fatness of F.

Theorem 7.2Let(f2M1×f1M2,F)be a DWP-complex Finsler manifold of two strongly convex complex Finsler manifolds(M1,F1)and(M2,F2).

(i)If(M1,F1)and(M2,F2)are locally projectively fat manifolds,then(f2M1×f1M2,F)is a locally projectively fat manifold if and only if the functions f1and f2are positive constants.

Proof(i)According to Proposition 7.1,(f2M1×f1M2,F)is locally projectively fat if and only if

Contracting(7.3)and(7.4)with respect to viand vi′,respectively,and compare the obtained equations,we get

Using(2.2),and notice(M1,F1)and(M2,F2)are projectively fat manifolds,we obtain

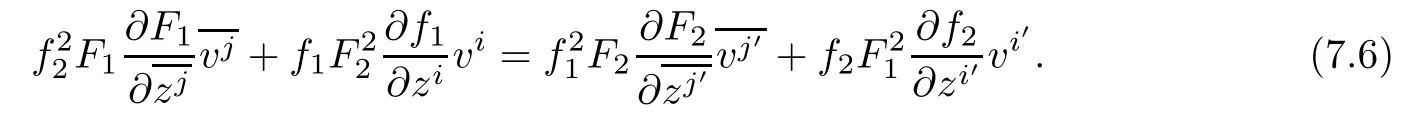
Diferentiating(7.6)with respect to vsand vt′,we get

Contracting(7.7)with respect to vsand vt′,we get

Since the left hand side of(7.8)depends only on(z1,v1),while the right hand side of(7.8) depends only on(z2,v2),it follows that

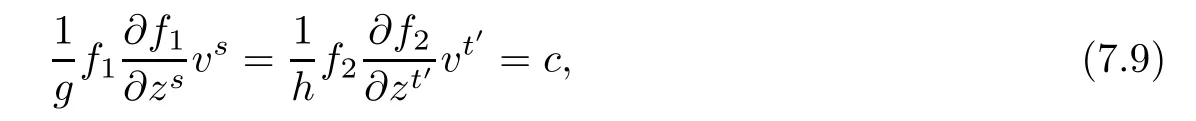
which implies that the functions f1and f2are positive constants.

(ii)According to Proposition 7.1,(f2M1×f1M2,F)is locally dually fat if and only if

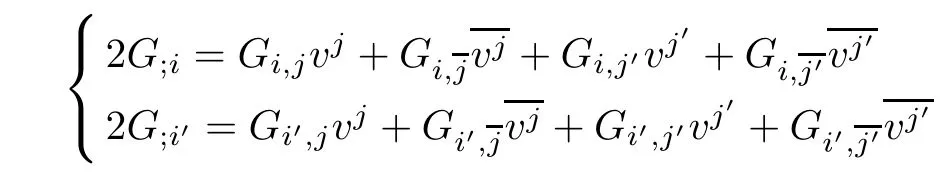
Using(2.2),and notice(M1,F1)and(M2,F2)are locally dually fat complex Finsler manifolds,we fnd that this is equivalent to

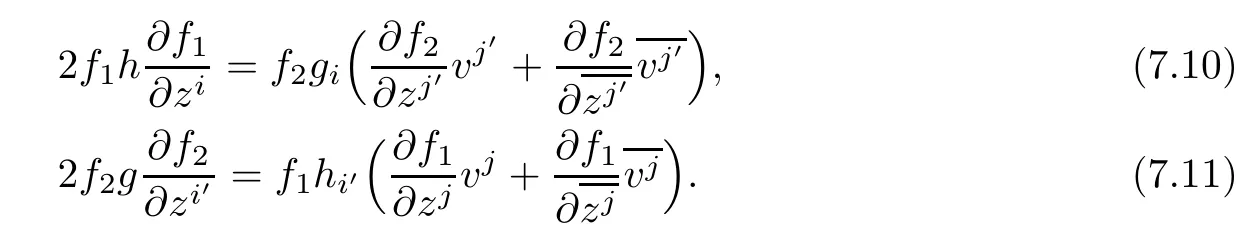
Contracting(7.10)and(7.11)with viand vi′,respectively,we obtain

Interchanging indices i and j of(7.13),and adding(7.12),we get

Since the left hand side of(7.14)is conjugate to the right hand side of(7.14),thus

is a real value function.

[1]Abate M,Patrizio G.Finsler Metrics—A Global Approach with Applications to Geometric Function Theory. Lecture Notes in Mathematics,Volume 1591.Berlin Aeidelberg:Springer-Verlag,1994

[2]Aikou T.On complex Finsler manifolds.Rep Fac Sci Kagoshima Univ(Math Phys&Chem),1991,24: 9–25

[3]Aikou T.Complex manifolds modeled on a complex Minkowski space.J Math Kyoto Univ(JMKYAZ), 1998,35-1:85–103

[4]Aikou T.Some remarks on locally conformal complex Berwald spaces.Contem Math,1996,196:109–120

[5]Aldea N,Munteanu G.On complex Landsberg and Berwald spaces.J Geom Phys,2012,62(2):368–380

[6]Asanov G S.Finslerian extensions of Schwarzschild metric.Fortschr Phys,1992,40:667–693

[7]Asanov G S.Finslerian metric functions over the product R×M and their potential applications.Rep Math Phys,1998,41:117–132

[8]Baagherzadeh Hushmandi A,Rezaii M M.On warped product Finsler spaces of Landsberg type.J Math Phys,2011,52,No.9093506.17

[9]Baagherzadeh Hushmandi A,Rezaii M M,Morteza M.On the curvature of warped product Finsler spaces and the Laplacian of the Sasaki-Finsler metrics.J Geom Phys,2012,62(10):2077–2098

[10]Bao D,Chern S S,Shen Z.An Introduction to Riemann-Finsler Geometry.GTM 200.Springer-Verlag, 2000

[11]Beem J K,Ehrlich P,Powell T G.Warped product manifolds in relativity in selected studies:a volume dedicated to the memory of Albert Einstein(T.M.Rassias and G.M.Rassias eds.).Armsterdarm:North-Holland,1982:41–56

[12]Bishop R L,O’Neill B.Manifolds of negative curvature.Trans Amer Math Soc,1969,145:1–49

[13]Chen B,Shen Y B.K¨ahler Finsler metrics are actually strongly K¨ahler.Chin Ann Math Ser B,2009,30(2): 173–178

[14]Chern S S,Shen Z.Riemann-Finsler geometry.World Scientifc,2005

[15]Hamel G.¨Uber die Geometrieen in denen die Geraden die K¨urzesten sind.Math Ann,1903,57:231–264 [16]Katanaev O M,Kl¨osch T,Kummer W.Global properties of warped solutions in general relativity.Ann Physics,1999,276:191–222

[17]Kobayashi S.Negative vector bundles and complex Finsler structures.Nagoya Math J,1975,57:153–166 [18]Kozma L,Peter I R,Varga C.Warped product of Finsler-manifolds.Ann Univ Sci Budapest,2001,44: 157

[19]Matsumoto M.Foundations of Finsler Geometry and Special Finsler Spaces.Kaiseisha Press,1986

[20]Matsumoto M.Remarks on Berwald and Landsberg spaces,in Finsler Geometry.Contem Math,1996,196: 79–82

[21]Munteanu G.Complex Spaces in Finsler,Lagrange and Hamilton Geometries.Kluwer Academic Publishers, 2004

[22]O’Neill B.Semi-Riemannian Geometry.New York:Academic Publisher,1983

[23]Peyghan E,Tayebi A.On doubly warped product Finsler manifolds.Nonlinear Anal Real World Appl, 2012,13(4):1703–1720

[24]Rund H.The curvature theory of direction-dependent connections on complex manifolds.Tensor N S,1972, 24:189–205

[25]Shen Z.On a class of Landsberg metrics in Finsler geometry.Can J Math,2009,61(6):1357–1374

[26]Shen Z.Riemann-Finsler geometry with applications to information geometry.Chin Ann Math Ser B,2006, 27(1):73–94

[27]Sun L,Zhong C.Characterizations of complex Finsler connections and weakly complex Berwald metrics. Diferential Geom Appl,2013,31:648–671

[28]Szabso Z I.All regular Landsberg metrics are Berwald.Ann Global Anal Geom,2008,34(4):381–386

[29]Szabso Z I.Correction to all regular Landsberg metrics are Berwald.Ann Global Anal Geom,2009,35(3): 227–230

[30]Unal B.Doubly Warped Products.Difer Geom Appl,2001,15(3):253–263

[31]Wong B.On the holomorphic curvature of some intrinsic metrics.Proc Amer Math Soc,1977,65:57–61

[32]Wu H.A remark on holomorphic sectional curvature.Indiana Univ Math J,1973,22:1103–1108

[33]Wu Z,Zhong C.Some results on product complex Finsler manifolds.Acta Math Sci,2011,31B(4):1541–1552

[34]Zhong C.On real and complex Berwald connections associated to strongly convex weakly K¨ahler-Finsler metric.Diferential Geom Appl,2011,29:388–408

[35]Zhong C.On unitary invariant strongly pseudoconvex complex Finsler metrics.Diferential Geom Appl, 2015,40:159–186

∗Received May 11,2015;revised December 22,2015.This work is supported by Program for New Century Excellent Talents in University(NCET-13-0510);National Natural Science Foundation of China(11271304, 11571288,11461064);the Fujian Province Natural Science Funds for Distinguished Young Scholar(2013J06001); the Scientifc Research Foundation for the Returned Overseas Chinese Scholars,State Education Ministry.