高 攀，方 威

(长沙理工大学交通运输工程学院，湖南 长沙 410004)

基于区间交叉熵的鲁棒最短路模型和算法研究

高 攀，方 威

(长沙理工大学交通运输工程学院，湖南 长沙 410004)

由于交通需求是区间数，路段阻抗也必然是区间数，这导致区间阻抗下的鲁棒最短路成为研究的核心问题。文章运用行为经济学的参照系理论，分别用下界与上界为阻抗，计算得到区间最短路，以此为参照，考虑最坏情形，构造鲁棒有效路径的两个判断标准，得到有效路径集合；运用交叉熵理论，计算有效路径与参照区间最短路的交叉熵，构建基于最小交叉熵的鲁棒最短路模型。

交叉熵；有效路径；鲁棒最短路；区间阻抗

0 引言

近年来，网络优化问题在运筹学中成了一项很重要的研究内容，它包括最短路问题、网络流问题、车辆路径问题和中国邮递员问题等等。最短路问题的重点是用最小的距离、时间或成本寻找一条从起点到终点的路，它是网络理论中的最基本问题。随着不确定理论在各个领域的不断推广与深化研究，在交通方面，考虑不确定性的交通分配问题也越来越受到国内外专家的关注。周和平等(2003、2005)分别将需求视为区间随机数与区间模糊数，运用模拟的反推技术，得到区间OD矩阵[1，2]，Bertsimas D等(2003)主要研究数据不确定离散优化以及能控制在保守度以内的网络流问题，为此建立了一个鲁棒整数规划模型[3]。最短路的选择是交通分配的基础，只有确定了最短路，才能进行之后的交通分配。所以，找寻最短路是交通分配中最重要、也最基础的一环。

本文考虑的是区间需求，这导致网络中的路段上阻抗也为区间值，这样就不能很轻松地得到网络上的最短路，因为区间数不是一个确定的数，并且在区间重叠的情况下也很难定义最短路。为此，本文将区间阻抗下的最短路问题转化为了最短路径行为选择问题。本文提出了参照最短路的概念，以参照最短路为评价标准，并利用实际最短路分布逼近参照最短路分布的特点，建立了交叉熵最短路模型，并给出了相应的求解算法。

1 区间阻抗下参照最短路定义

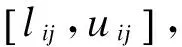
(1)网络中只有一个起点和一个终点，并且是无循环的；

(2)网络中任意弧段上的阻抗都是相互独立的；

(3)区间阻抗是服从正态分布的随机变量。

在定义参照最短路之前，需注意上界最短路和下界最短路。对于一个区间阻抗下的不确定性网络，当把阻抗全部取区间上界时，得到一个确定性的网络，这时的最短路就是上界最短路；当把阻抗全部取区间下界时，得到另一个确定性的网络，这时的最短路就是下界最短路。分别取上界最短路的上界和下界最短路的下界，得到一条虚拟路径，即参照最短路。

为了对参照最短路的定义进行更好的解释，以下给出一个简单的有向网络图(见图1)，该网络由4个节点5个路段组成，其中r为起点，s为终点，弧边上的数据表示路段上的区间阻抗值。

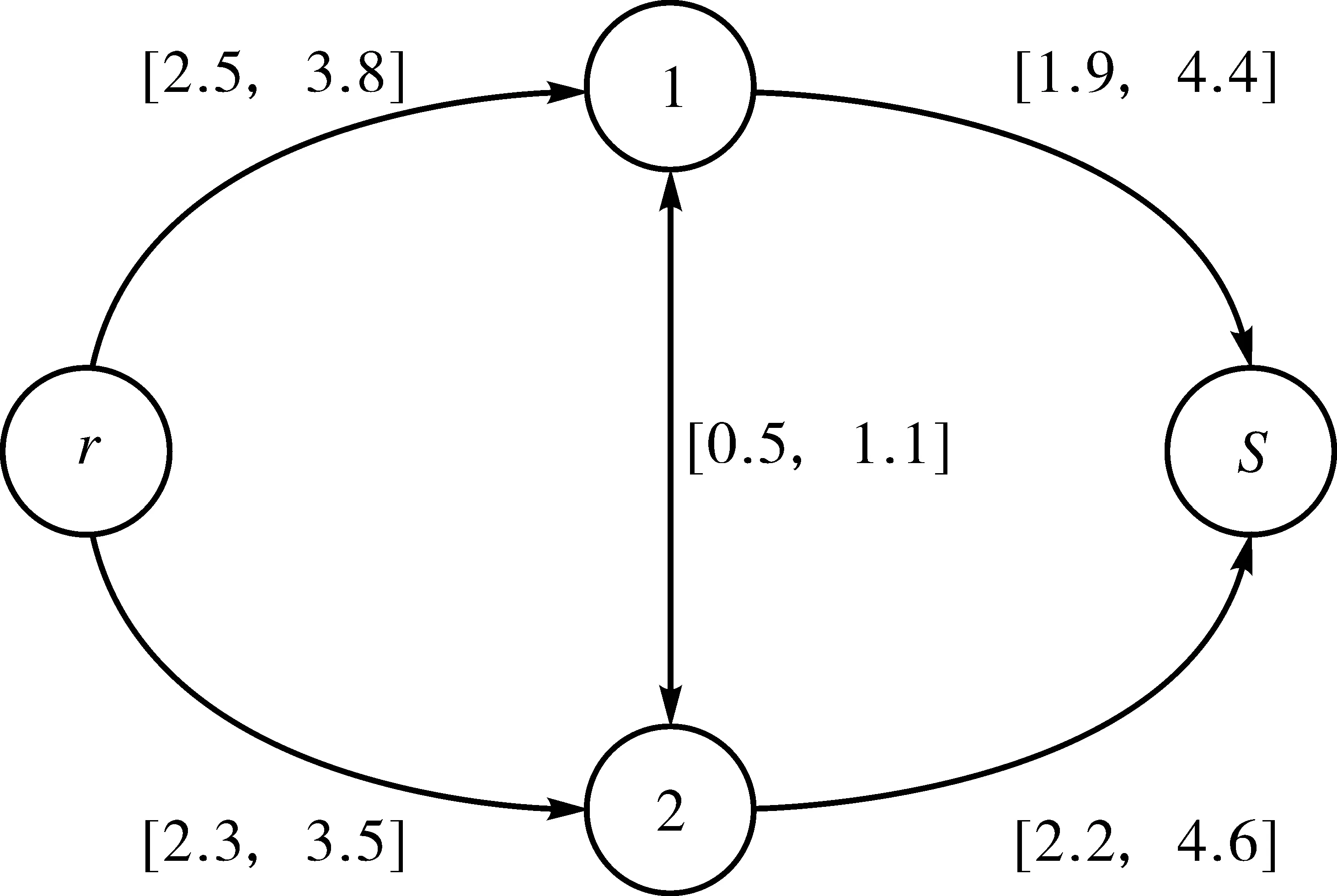
图1 简单区间网络图

当路段阻抗全部取区间上界时，可得图2。

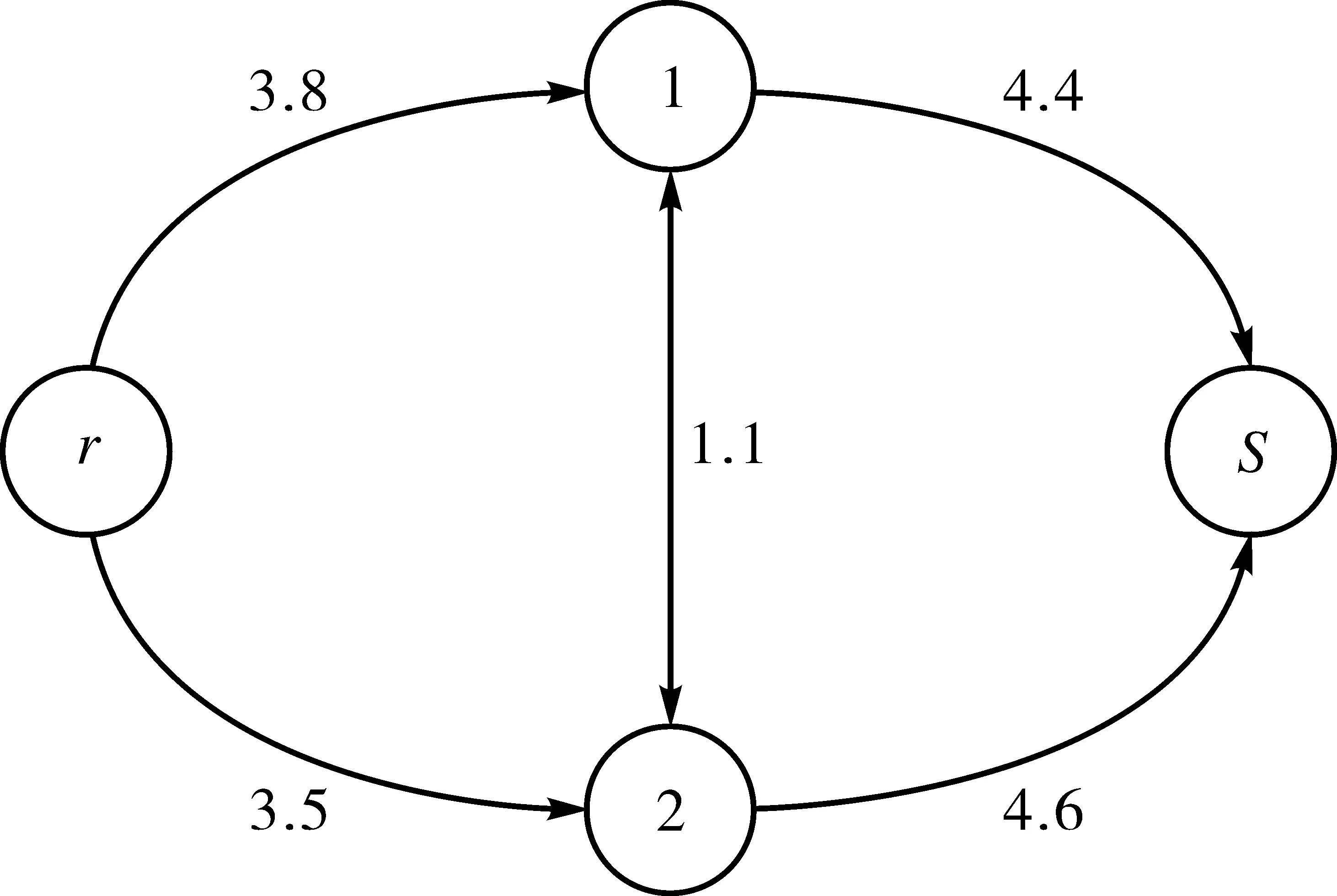
图2 区间上界网络图

由图2可知，图1的上界最短路为r-2-s，路径区间阻抗为[4.5，8.1]。

当路段阻抗全部取区间下界时，可得图3。

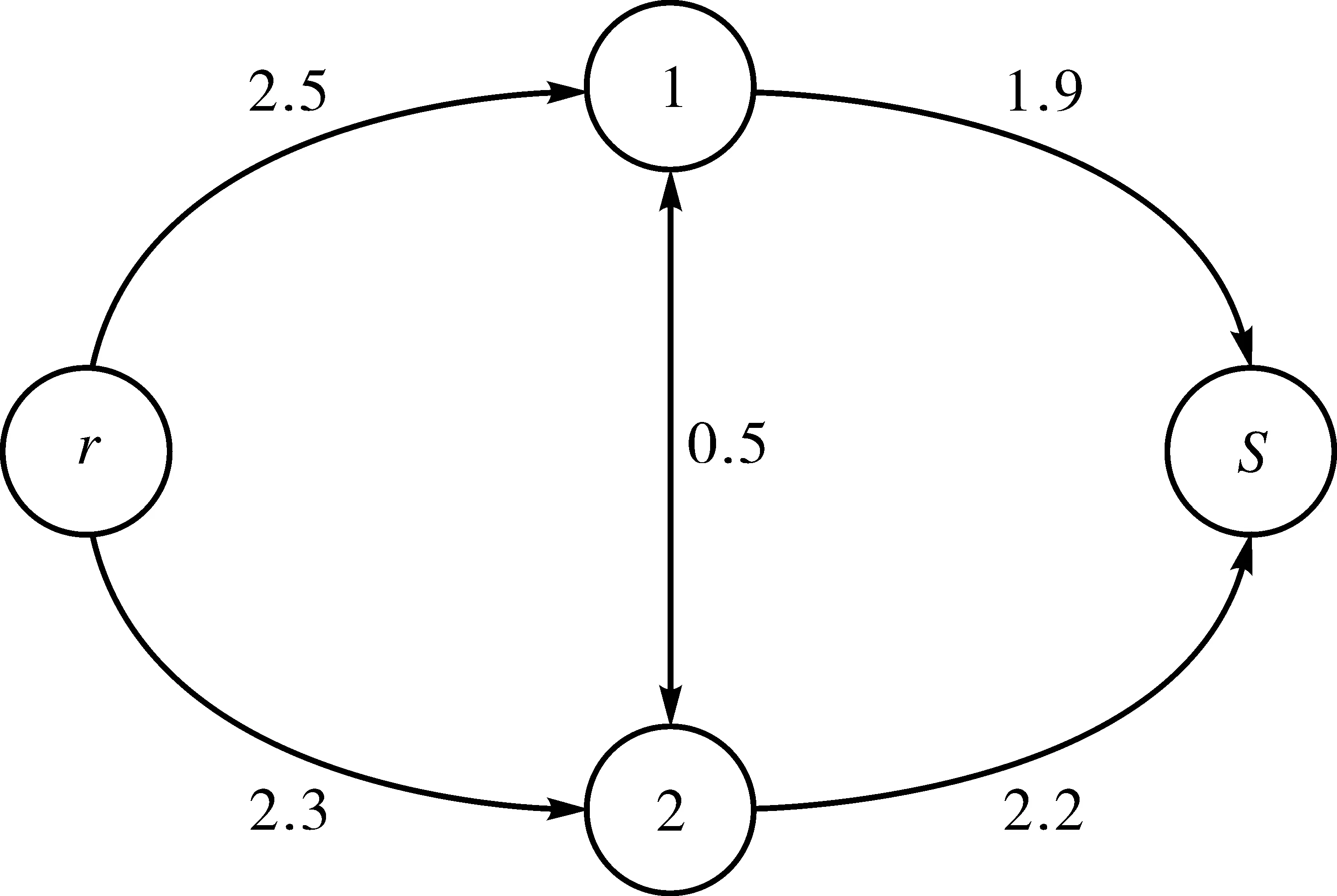
图3 区间下界网络图

由图3可知，图2的下界最短路为r-1-s，路径区间阻抗为[4.4，8.2]。

根据上述定义，由下界最短路的下界和上界最短路的上界就构成了参照最短路的路径区间阻抗，因此图2中参照最短路的路径区间阻抗为[4.4，8.1]。

2 区间阻抗下鲁棒有效路径判断的两个标准

关于有效路径的定义，传统有效路径的定义是：当路段(i，j)的上游端点i比下游端点j距离起点r更近，同时又有i比j距离终点s更远，则该路段可以成为有效路段，由有效路段组成的可行路径即有效路径[4，5]。黄海军等(2003)考虑到实际交通网络中流量非常小的路径不会影响最后的交通分配，重新定义了有效路径[6]。秦鸣等(2010)介绍了三种有效路径的定义方法并做了比较，对于确定阻抗下的有效路径搜寻有一定实际意义，但对于区间阻抗下的有效路径依然无能为力[7]。在本研究中，网络中的路段阻抗是不确定的，是一个区间数，因此本文提出了鲁棒有效路径的概念。

鲁棒有效路径是由鲁棒有效节点组成的路径，而鲁棒有效节点的判断可以依照以下两个标准。(1)从i出发选择下一节点j，如果选择不当，i-j阻抗取区间上界值，那么j-s的阻抗取下界最短路的阻抗。此时，应满足j-s的阻抗加上i-j的阻抗比i-s的上界最短路阻抗值要小；(2)从i出发选择下一节点j，如果选择得当，i-j阻抗取区间下界值，那么j-s的阻抗取上界最短路的阻抗。此时，同样应满足j-s的阻抗加上i-j的阻抗比i-s的上界最短路阻抗值要小。如果同时满足这两个标准，便成为所寻找的鲁棒有效节点。鲁棒有效节点可以用公式(1)、(2)进行判断：

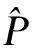
(1)

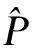
(2)

式中，lij，uij——分别为路段(i，j)阻抗的下界、上界值；

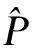
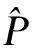
为了对鲁棒有效路径的定义进行更好的解释，仍以图1为例进行简单的判断：

从r开始选择下一节点。对于节点1：

标准一：2.5+4.4<8.1，符合；

标准二：3.8+1.9<8.1，符合。

因此对于r而言，节点1是鲁棒有效节点。

从节点1开始选择下一节点，如果选择终点s，选择结束，则r-1-s为鲁棒有效路径；如果选择节点2，对于节点2：

标准一：0.5+4.6>4.2，不符合；

标准二：1.1+2.2<4.2，符合。

因此对于节点1而言，节点2不是鲁棒有效节点，则r-1-2-s不是鲁棒有效路径。其它有效节点的判断与此类似，不一一判断。

3 区间阻抗下最短路模型的构建

(1)参数定义

N：网络中所有节点的集合，包括起点r和终点s；

A：网络中节点间路段的集合；

i，j，k：网络中节点的记号；

lij，uij：分别为路段(i，j)阻抗的下界值、上界值；

xij：0-1决策变量，当路段(i，j)被选中取值1，反之则取值0；

Prs：r到s任意路径；

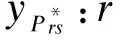
yPrs：r到s任意路径的路径阻抗；

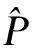
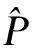
(2)目标函数

对于确定性边权的最短路问题，一般就是将边权作为评价指标，那么具有最小边权的路径即为最短路径。本文中边权为区间数，各条路径之间无法直接比较，为了解决这个问题，运用行为经济学中的参照系理论，特引入了参照最短路的概念。以参照最短路为评价标准，在假设路径阻抗值服从正态分布的基础上，与参照最短路分布最接近的鲁棒有效路径即认为是鲁棒最短路径，根据以上描述，运用交叉熵理论构建模型，数学表达式为：

(3)

(3)约束条件

①平衡流约束，即保证所选择的路段构成了一条从起点到终点的完整连通路径。

(4)

②有效节点约束，保证选取的路径是鲁棒有效路径。

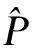
基于以上的定义及相关描述，区间阻抗下的网络最短路问题可以建立以下模型：

(5)

以上模型为本文建立的鲁棒最短路模型，该模型很好地描述了具有区间阻抗下的网络最短路问题，减少了网络的不确定性，又保留了最大的不确定性。以下将探讨此模型的求解。

4 最短路算法设计

最短路算法是设计交通分配算法的基础，其目的是找到起点到终点之间的最短路径，传统方法用的是Dijkstra算法和Floyd算法。两者的区别在于：Dijkstra算法只可以求解网络中某一固定节点到另一节点之间的最短路，而Floyd算法可以算出网络中任意一对起、终点之间的最短路。由于本文中涉及到路段阻抗为区间值，传统算法无法进行有效计算，因此本文将运用交叉熵理论，设计解决区间阻抗下网络的最短路问题，相关计算步骤如下：

步骤1：对区间阻抗下的网络全取区间上界，然后用Dijkstra算法求得上界最短路，同理，全取区间下界可得到下界最短路；

步骤2：通过上界最短路和下界最短路确定参照最短路，并以此为评价标准；

步骤3：按照鲁棒有效节点的两个判断标准，找到所有鲁棒有效路径；

步骤4：使所有的鲁棒有效路径与参照最短路进行比较，得到熵最小的即为鲁棒最短路；

步骤5：计算结束，输出OD对间的鲁棒最短路。

5 算例分析

为了对上述算法进行详细介绍，以图4为例进行计算：

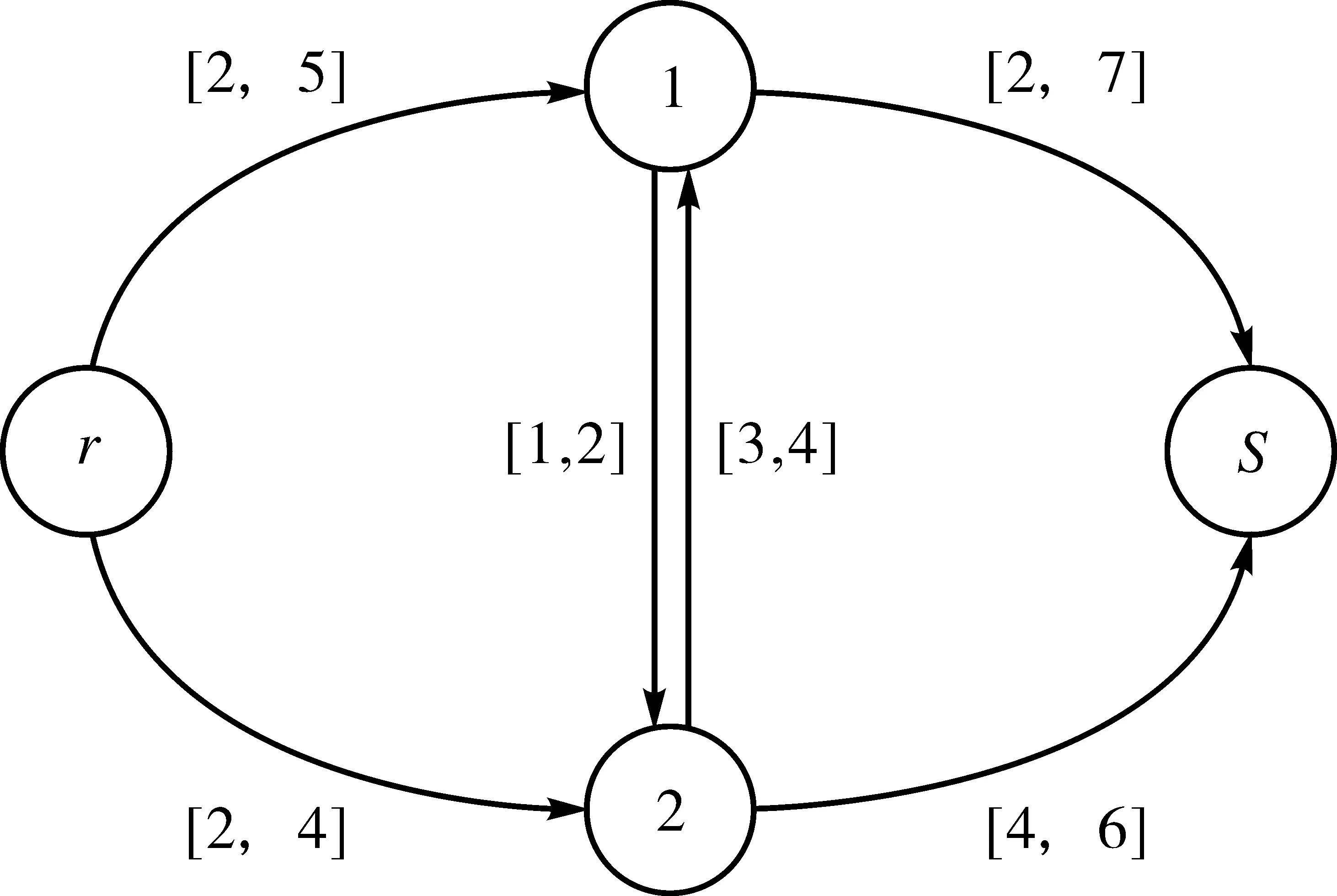
图4 算例分析图

Step1：对区间阻抗下网络分别取上、下界值，用Dijkstra算法求得上界最短路与下界最短路：r-2-s，r-1-s；其路径阻抗分别为[6，10]，[4，12]；

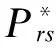
Step3：通过鲁棒有效节点的判断标准，找到所有鲁棒有效路径r-1-s，r-2-s，r-1-2-s；

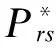
Step5：计算结束，图4的鲁棒最短路为r-1-s。

为了验证算法的有效性，下面采取鲁棒优化理论中常用的两个标准，鲁棒偏差标准和相对鲁棒标准来对图4的最短路进行计算。

方法一，以鲁棒偏差标准进行计算：

Step1：找出网络中鲁棒有效路径：r-1-s，r-2-s，r-1-2-s；

Step2：定义鲁棒成本，任意选择一条路径，此路径上的路段阻抗全取上界值，其余路段阻抗全取下界值得到一条最短路，鲁棒成本就是所选路径阻抗与最短路阻抗的差；

Step3：计算鲁棒有效路径的鲁棒成本，R(r-1-s)=6，R(r-1-2-s)=6，R(r-2-s)=6；

Step4：计算结束，鲁棒成本最小的即为鲁棒最短路，因此，以鲁棒偏差标准无法得到图4的鲁棒最短路。

方法二，以相对鲁棒标准进行计算：

Step1：找出网络中鲁棒有效路径：r-1-s，r-2-s，r-1-2-s；

Step2：定义鲁棒成本，任意选择一条路径，此路径上的路段阻抗全取上界值，其余路段阻抗全取下界值得到一条最短路，鲁棒成本就是所选路径阻抗与最短路阻抗的差；

Step3：计算鲁棒有效路径的鲁棒成本，R(r-1-s)=6，R(r-1-2-s)=6，R(r-2-s)=6；

Step4：计算鲁棒有效路径的鲁棒成本与此情景下最短路阻抗的比值，R(r-1-s)=6/6=1，R(r-1-2-s)=6/7=0.86，R(r-2-s)=6/4=1.5；

Step5：计算结束，比值最小的即为鲁棒最短路，因此，以相对鲁棒标准得到图4的鲁棒最短路为r-1-2-s。

基于图4对三种方法进行比较，本文找出的鲁棒最短路为r-1-s，路径阻抗为[4，12]；相对鲁棒方法找出的鲁棒最短路为r-1-2-s，路径阻抗为[7，13]；鲁棒偏差方法无法得到鲁棒最短路。从直观上判断，路径r-1-s更符合人们的行为选择，因此本文提出的基于交叉熵模型的算法在寻找最短路时有一定的优势。

6 结语

本文在分析传统最短路问题的基础上，考虑区间阻抗下网络的特殊性，提出了上界最短路、下界最短路以及参照最短路的概念，并针对传统有效路径提出了鲁棒有效路径的概念，根据交叉熵的理论，建立了鲁棒最短路模型，并设计了对应的求解算法，有效地解决了区间阻抗下的网络最短路问题。

[1]周和平，晏克非，胡列格.基于随机模拟的遗传算法在OD反推中的应用研究[J].系统工程，2003，21(4)：115-119.

[2]周和平，晏克非，胡列格.基于随机模糊路段流量的OD反推的不确定规划模型与算法研究[J].铁道科学与工程学报，2005，2(5)：69-74.

[3]BertsimasD，SimM.Robustdiscreteoptimizationandnetworkflows[J].Mathematicalprogramming，2003，98(1-3)：49-71.

[4]赖树坤，姚宪辉，彭 愚.交通网络中有效路径确定方法的探讨[J].交通标准化，2008(1)：137-140.

[5]YangXF，LiuLF，Yin-ZhenaLI，etal.DeterminingtheEfficientPathsBasedonEffectDegree[J].JournalofTransportationSystemsEngineering&InformationTechnology，2011，11(6)：104-110.

[6]李志纯，黄海军.随机交通分配中有效路径的确定方法[J].交通运输系统工程与信息，2003，3(1)：28-32.

[7]秦 鸣，姜 培.基于有效路径的多路径交通流分配[J].交通标准化，2010(7)：30-33.

Research on Robust Shortest Path Model and Algorithm Based on Interval Cross Entropy

GAO Pan，FANG Wei

(School of Traffic and Transportation Engineering，Changsha University of Science &Technology，Changsha，Hunan，410004)

As the traffic demand is the interval number，and the road segment impedance must also be the interval number，which leads to the robust shortest path under interval impedance becoming the core research problem.By using the reference frame theory of behavioral economics，this article respectively used the lower bound and upper bound as the impedance，calculated the interval shortest path，which were used as the reference，and considering the worst case，it constructed two judgment criteria of robust effective path，and obtained the effective path set；by using the cross entropy，it calculated the cross-entropy between the effective path and the reference interval shortest path，and constructed the robust shortest path model based on minimum cross-entropy.

Cross entropy；Effective path；Robust shortest path；Interval impedance

高 攀(1993—)，在读硕士研究生，研究方向：交通运输规划与管理；

方 威(1991—)，在读硕士研究生，研究方向：交通运输规划与管理。

交通运输部应用基础研究项目(2014319825 190)

U491

A

10.13282/j.cnki.wccst.2016.12.017

1673-4874(2016)12-0057-05

2016-10-26