有关垂足三角形几个最值猜想的证明*

2016-12-01蒋荣清

中学教研(数学) 2016年3期

关键词：条边外接圆共线

●蒋荣清

(台州市教育局教研室浙江台州 318000)

有关垂足三角形几个最值猜想的证明*

●蒋荣清

(台州市教育局教研室浙江台州 318000)

△DEF为锐角△ABC内点P对应的垂足三角形，记三角形的面积、周长、外接圆半径分别为S,L,R.笔者证明了当点P为△ABC的外心时，S最大；当点P为△ABC的垂心时，L最小；当点P为△ABC的内心时，R最小．

锐角三角形；垂足三角形；最值

定义如图1，在△ABC中，过点P分别作PD,PE,PF垂直AB，BC,CA于点D,E,F，联结DE,EF,FD，则称△DEF为△ABC的垂足三角形．

图1 图2

对于垂足三角形，在文献[1]中提出了4个猜想：

猜想如图1，△DEF为锐角△ABC内点P对应的垂足三角形，记△DEF的面积、周长、外接圆半径、内切圆半径分别为S,L,R,r，则

1)当点P为△ABC的外心时，S最大；

2)当点P为△ABC的垂心时，L最小；

3)当点P为△ABC的内心时，R最小；

4)当点P为△ABC的重心时，r最大．

对于猜想4)已寻找到反例，因此一般情形不成立．下面证明猜想1)～3).

1 猜想1)的证明

证法1 如图2，设⊙O为△ABC的外接圆，且半径为R，OP=d，AP的延长线交⊙O于点M.因为∠AFP=∠ADP=90°，所以点A，D，P，F共圆，且AP是这个圆的直径，从而∠PAD=∠PFD.由正弦定理得

从而DF=AP·sin∠BAC,

(1)

同理可得 ∠PBE=∠PFE，EF=BP·sin∠ABC，

(2)

于是

∠DFE=∠PFD+∠PFE=∠PAD+∠PBE=∠CBM+∠PBE=∠PBM.

在△PBM中，由正弦定理得

从而

因此PM·sin∠ACB=BP·sin∠DFE.

(3)

由式(1)～(3)得

又△ABC为锐角三角形，由圆幂定理得AP·PM=R2-d2,

于是

由于sin∠BAC·sin∠ABC·sin∠ACB为正的定值，且R也是一个定值，因此当d=0，即点P与点O重合时，S△DEF的面积最大.

图3

引理1 如图3，△ABC为锐角三角形，⊙O是它的外接圆，半径为R．设A(R,0)，B(Rcosα,Rsinα)，C(Rcosβ,-Rsinβ)(其中0<α<π，0<β<π),点P(a,b)在△ABC内，△DEF是对应于点P(a,b)的△ABC的(广义)垂足三角形，|PO|=d，记△ABC，△DEF的面积分别为S′,S，则

同理可得

因此

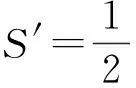
因为

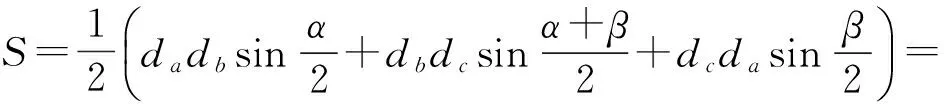
下面给出猜想1)的第2种证法：

图4

2 猜想2)的证明

如图4，H是△ABC的垂心,K,M,N分别是边AB,AC,BC上的垂足，点F关于直线BC的对称点为F′，则EF=EF′，∠FCE=∠F′CE．在直线F′C上取点M′，使∠MNC=∠M′NC，则在△MNC和△M′NC中，

∠FCE=∠F′CE, ∠MNC=∠M′NC,NC=NC,

即△MNC≌△M′NC，从而MN=M′N.同理可得，设点F关于直线AB的对称点为F″，则DF=DF″．在直线F″A上存在点M″，使得

∠M″KA=∠MKA,MK=M″K,

因此△DEF的周长为L=F″D+DE+EF′，△KMN的周长为L′=M″K+KN+NF′．

(事实上，点M′,N,K,M″共线．因为点M,H,N,C共圆，所以∠HNM=∠HCM,同理可得∠HNK=∠HBK.又∠HCM=∠HBK=90°-∠BAC，于是∠HNM=∠HNK，而∠MNC=∠M′NC，∠HNM+∠MNC=90°，则点K,N,M′共线．同理可得，点K,N,M″共线，故点M′,N,K,M″共线．)因此，△KMN的周长L′=M′M″，而△DEF的周长L=F″D+DE+EF′≥F′F″，至此原问题化为只需证明F′F″≥M′M″即可．由前面的证明知

∠NM′C=∠NMC, ∠KM″A=∠KMA,

又∠NMC=∠KMA，从而∠NM′C=∠KM″A,于是△OM′M″为等腰三角形，故OM′=OM″．

因为F′M′=FM，F″M″=FM,所以F′M′=F″M″.设OM′=OM″=x，F′M′=F″M″=y，∠AOC=α．由余弦定理得

从而

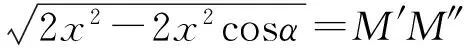
故F′F″≥M′M″,即猜想2)成立．

3 猜想3)的证明

设△DEF的外接圆圆心为O，则⊙O与△ABC的3条边必有公共点，也即⊙O与△ABC的3条边相交或相切．因此可将问题分成4类：①⊙O与△ABC的3条边都相切；②⊙O与△ABC的2条边相切、1条边相交；③⊙O与△ABC的1条边相切、2条边相交；④⊙O与△ABC的3条边都相交．当点P为△ABC的内心时，记此时△DEF的外接圆半径为R0．只需证明另外3种情形的R≥R0即可．