芦存博 肖 嵩 权 磊



基于二进制序列族的压缩感知测量矩阵构造

芦存博*肖 嵩 权 磊

(西安电子科技大学ISN国家重点实验室 西安 710071)

构造确定性测量矩阵对压缩感知理论的推广与应用具有重要的意义。该文源于代数编码理论，提出一种基于二进制序列族的确定性测量矩阵构造算法。相关性是描述矩阵性质的重要准则，减小相关性可使重建性能提高。该文推导出所构造测量矩阵的相关性小于同条件下的高斯随机矩阵和伯努利随机矩阵。理论分析和仿真实验表明，该方式构造的测量矩阵的重建性能优于同条件下的高斯随机矩阵和伯努利随机矩阵；所构造矩阵可由线性反馈移位寄存器结构实现，易于硬件实现，有利于压缩感知理论的实用化。

信号处理；压缩感知；测量矩阵；二进制序列族

1 引言

压缩感知(Compressed Sensing, CS)[1,2]的概念是2006年Donono和Candes等人提出的，它是一种不同于奈奎斯特(Nyquist)采样定律的全新信号采样框架。CS可实现以远低于Nyquist的采样率去采样稀疏信号，其核心是利用测量矩阵将高维稀疏信号投影到一个低维空间上，然后利用信号的稀疏性，通过重建算法以高概率实现原始信号的精确重建。这种提高采样效率的新思路引起了学术界的广泛关注，CS在数字信号处理、信息论、通信、光学成像、雷达等领域受到高度关注。

CS过程分为两部分：数据采样和信号重建，在这两部分中测量矩阵都起着至关重要作用。首先，在数据采样中，好的测量矩阵可以以较少的测量数目达到相同的重构精度。其次，在信号重建中，在相同的采样率下得到的数据，好的测量矩阵对信号可以达到较高的重构精度。总体来说，好的测量矩阵能够在投影测量时保持原始信号的全部信息，并可结合测量值重构出原始信号。测量矩阵的性质决定了能否将原始信号的全局信息保存下来。文献[3]提出了测量矩阵必须满足的性质-约束等距性(Restricted Isometry Property, RIP), 即只要测量矩阵满足RIP特性，那么就能以高概率从低维的测量结果向量中准确地恢复出原信号。相关性(coherence)是建立矩阵RIP的另一个重要方法，文献[4]指出了相关性跟RIP的关系：低相关性的矩阵满足RIP。矩阵的RIP[5,6]和相关性均是分析测量矩阵性质的重要工具，本文将采用相关性对所构造测量矩阵的性质进行分析和说明。

测量矩阵可以分为随机测量矩阵和确定性测量矩阵。在随机矩阵中比较常用的是高斯矩阵和伯努利矩阵。由于随机矩阵能够以很大概率满足RIP, 因此在科研上被广泛应用。但是在随机矩阵中，每一个元素都是独立同分布的，存在不确定性，使得每一个元素都要存储，耗费大量的存储资源，并且随机数的产生对硬件要求很高，不利于硬件实现，使得其实际应用受限。确定性测量矩阵的元素和值都是确定的，可以克服这些不足。许多研究者利用一些技术来构造确定性测量矩阵。例如，文献[7]指出好的原模图低密度奇偶校验码(Low Density Parity Check, LDPC)校验矩阵可以作为测量矩阵；文献[8]采用m序列构造出性能较好的测量矩阵；文献[9]利用Berlekamp-Justesen码构造测量矩阵；文献[10]采用范德蒙矩阵构造出性能较好的测量矩阵；文献[11]用混沌序列构造测量矩阵；文献[13]用Reed- Solomon码构造测量矩阵等。

本文将在文献[14]中二进制序列族(Binary Sequence Family, BSF)的基础上构造一种确定性测量矩阵(Binary Sequence Family based Deterministic Measurement Matrix, BSFDMM)，它是一种由+1和-1组成的双极性矩阵，并推导出了矩阵BSFDMM的相关性小于同条件下的高斯随机矩阵和伯努利随机矩阵。理论分析和仿真实验表明，文中矩阵BSFDMM的重建性能优于同条件下的高斯随机矩阵和伯努利随机矩阵。

2 基本理论

2.1 压缩感知

上述求解问题是NP-hard。CS理论证明了在适当的测量矩阵下，该问题可以转化为求解最小1范数优化问题，即

该问题可以通过基追踪(Basis Pursuit, BP)算法[15]，得到与式(1)等价的最稀疏估计。目前，有一些直接求解式(1)的贪婪追踪类算法，该类算法通过迭代求解局部最优解，最终逼近全局最优，从而得到原始信号的精确估计。例如，正交匹配追踪(Orthogonal Matching Pursuit, OMP)[16]。

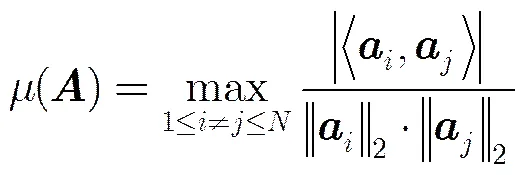
2.2 迹函数

3 测量矩阵构造

本文矩阵BSFDMM的具体实现步骤如下：

一旦给定数值转换函数式(5)和有限域上的迹表示函数式(3)或式(4)，则能确定出所构造矩阵的每一个元素值，避免了随机矩阵的不确定性；BSFDMM矩阵的元素结构使其非常便于硬件实现，数值转换函数式(5)的本质是元素替换，在硬件实现上只用改变相应元素的输出即可，非常简单；又因为矩阵BSFDMM的生成过程中，使用的是文献[14]的迹表示函数，从文献[14]可得，BSFDMM矩阵可由LFSR结构实现，易于硬件实现，有利于压缩感知理论的实用化。

4 相关性分析

相关性是描述矩阵性质的重要准则，减小相关性可使重建性能提高。本节给出所构造矩阵BSFDMM的相关性大小的上界，并推导出矩阵BSFDMM的相关性小于同条件下的高斯随机矩阵和伯努利随机矩阵，进而可从理论上证明矩阵BSFDMM的重建性能优于同条件下的高斯随机矩阵和伯努利随机矩阵。

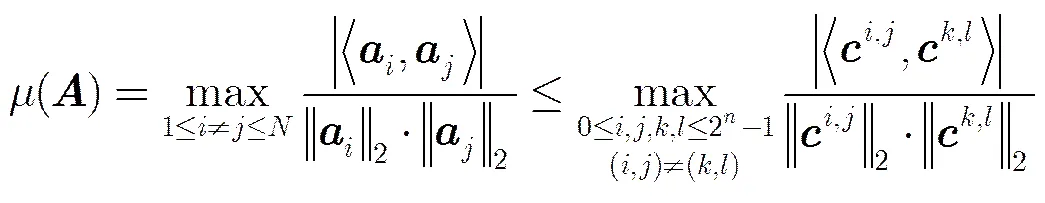
为了比较本文中的BSFDMM和同条件下的高斯随机矩阵和伯努利随机矩阵的重建性能，可以比较它们的相关性大小。首先引入以下文献[18]的两个引理：

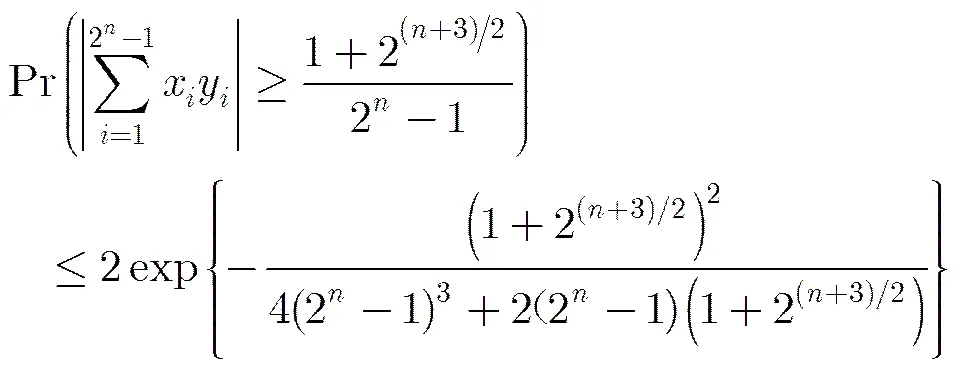
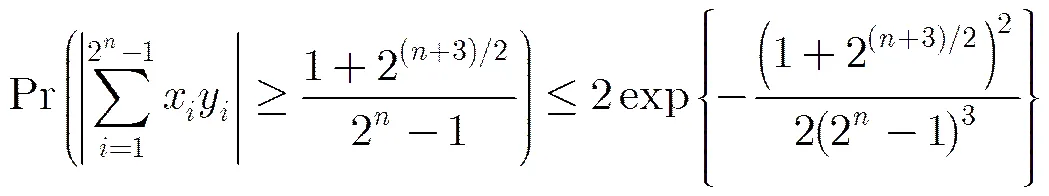
减小相关性能使可重建信号的稀疏度增大，重建性能提高。由定理1和定理2可以得到以下结论：

结论2 矩阵BSFDMM的重建性能优于同条件下的高斯随机矩阵。

结论3 矩阵BSFDMM的重建性能优于同条件下的伯努利随机矩阵。

5 实验仿真及分析

比较了本文矩阵BSFDMM与相同大小的高斯随机测量矩阵Gauss和伯努利随机测量矩阵Bernoulli在无噪声条件和有噪声条件下的重建性能，其中矩阵BSFDMM分为两种情况：(1)对应于是偶数的情况，此时矩阵大小为；(2)对应于是奇数的情况，此时矩阵大小为。通过随机选取支撑位置，且支撑值服从标准的高斯分布，来生成被采样的稀疏信号，其长度为。对每个稀疏度，用MATLAB生成1000次，重构算法选取OMP算法，若重建结果满足，则重建实验成功，重建概率即为精确重建次数与总次数的比值。Gauss矩阵的每一个元素取值服从独立同分布的标准正态分布。Bernoulli矩阵的每一个元素取值服从独立同分布的贝努利分布，且元素由+1和-1组成。

5.1无噪声重建

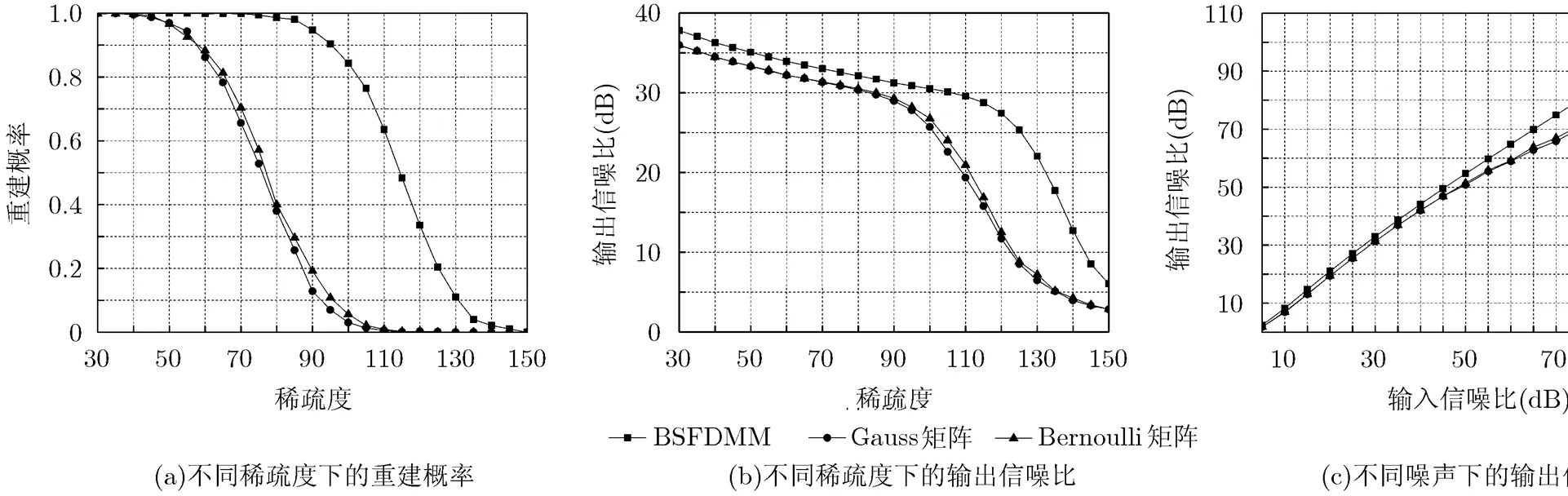
图1 BSFDMM大小为255512的情况

由图1(a)的重建曲线可以看出，对于矩阵BSFDMM，当信号稀疏度达到60时，才开始出现重建失败的情况。然而，相同大小的Gauss矩阵和Bernoulli矩阵在稀疏度分别为35和30时，就已经开始出现重建失败的情况。当信号稀疏度分别增大到130和125时，Gauss矩阵和Bernoulli矩阵就完全不能重建出原始信号。而矩阵BSFDMM在信号稀疏度增大到145时，依然有重建的可能。

从图2(a)的重建曲线可以看出，对于矩阵BSFDMM，当信号稀疏度达到30时，才开始出现重建失败的情况。然而，相同大小的Gauss矩阵和Bernoulli矩阵在稀疏度都为15时，就已经开始出现重建失败的情况。当信号稀疏度增大到70时，Gauss矩阵和Bernoulli矩阵两者都完全不能重建出原始信号。而矩阵BSFDMM在信号稀疏度增大到80时，依然有重建的可能。

从图1(a)和图2(a)的边界条件分析可见，矩阵BSFDMM的信号恢复效果比相同大小的Gauss矩阵和Bernoulli矩阵效果好，这是因为矩阵BSFDMM的相关性小于相同大小的Gauss矩阵和Bernoulli矩阵，可重建信号的稀疏度增大，重建性能提高。

5.2有噪声重建

图2 BSFDMM大小为127256的情况

从图1(b)和图2(b)可以看出，矩阵BSFDMM的信号恢复效果比相同大小的Gauss矩阵和Bernoulli矩阵效果好，这是因为矩阵BSFDMM的相关性小于后两者，更有利于信号重构。

从图1(c)和图2(c)可知，在不同输入噪声条件下，采用本文所构造的BSFDMM矩阵，进行重建后的输出信噪比比采用高斯随机测量矩阵和伯努利随机测量矩阵的都要高。随着输入信噪比的增加，3种矩阵的输出信噪比都随之增加。在图1(c)中，当输入信噪比小于40 dB时，由于噪声的影响，3种矩阵的输出信噪比曲线整体区分并不是非常明显，而从输入信噪比大于40 dB开始，3种矩阵的输出信噪比曲线区分开始明显，此时BSFDMM矩阵相关性小的优势开始明显体现。随着输入信噪比的增加，BSFDMM矩阵的输出信噪比曲线与其它两种矩阵的曲线的区分越来越明显。从图2(c)中也可以得到3种矩阵输出信噪比曲线类似的规律。

通过上述仿真发现，BSFDMM矩阵比相同条件下的高斯随机矩阵和伯努利随机矩阵的抗噪声性能都要好，说明本文矩阵不仅在无噪声条件下表现良好，在噪声环境中同样具有良好的重建性能，即表明文中所提矩阵的实用性。

6 结论

在二进制序列族的基础上，本文构造了一种确定性测量矩阵- BSFDMM，它是一种由+1和-1组成的双极性矩阵，并通过理论推导，得到所构造矩阵的相关性小于同条件下的高斯随机矩阵和伯努利随机矩阵。理论分析和仿真实验表明，在相同条件下，BSFDMM矩阵不仅在无噪声条件下的重建性能优于高斯随机矩阵和伯努利随机矩阵，而且在噪声环境下其抗噪声性能也比高斯矩阵和伯努利矩阵要好，说明了文中矩阵的实用性。矩阵BSFDMM可由LFSR结构实现，易于硬件实现，有利于压缩感知理论的实用化。

[1] CANDES E J, ROMBERG J, and TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]., 2006, 52(2): 489-509. doi: 10.1109/TIT.2005.862083.

[2] DONOHO D L. Compressed sensing[J]., 2006, 52(4): 1289-1306. doi: 10.1109 /TIT.2006.871582.

[3] CANDES E J and TAO T. Decoding by linear programming [J]., 2005, 51(12): 4203-4215. doi: 10.1109/TIT.2005.858979.

[4] BOURGAIN J, DILWORTH S, FORD K,. Explicit constructions of RIP matrices and related problems[J]., 2011, 159(1): 145-185. doi: 10.1215/ 00127094-1384809.

[5] GAN H, LI Z, LI J,. Compressive sensing using chaotic sequence based on chebyshev map[J]., 2014, 78(4): 2429-2438. doi: 10.1007/s11071-014-1600-1.

[6] CASTORENA J and CREUSERE C D. The restricted isometry property for banded random matrices[J]., 2014, 62(19): 5073-5084. doi: 10.1109/TSP.2014.2345350.

[7] ZHANG J, HAN G, and FANG Y. Deterministic construction of compressed sensing matrices from protograph LDPC codes[J]., 2015, 22(11): 1960-1964. doi: 10.1109/LSP.2015.2447934.

[8] 党骙, 马林华, 田雨, 等. m序列压缩感知测量矩阵构造[J].西安电子科技大学学报, 2015, 42(2): 186-192. doi: 10.3969/ j.issn.1001-2400.2015.02.031.

DANG Kui, MA Linhua, TIAN Yu,. Construction of the compressive sensing measurement matrix based on m sequences[J]., 2015, 42(2): 186-192. doi: 10.3969/j.issn.1001-2400.2015.02.031.

[9] 夏树涛, 刘璐, 刘鑫吉. 基于Berlekamp-Justesen码的压缩感知确定性测量矩阵的构造[J]. 电子与信息学报, 2015, 37(4): 763-769. doi: 10.11999/JEIT140875.

XIA Shutao, LIU Lu, and LIU Xinji. Deterministic constructions of compressive sensing matrices based on berlekamp-justesen codes[J].&, 2015, 37(4): 763-769. doi: 10. 11999/JEIT140875.

[10] 赵瑞珍, 王若乾, 张凤珍, 等. 分块的有序范德蒙矩阵作为压缩感知测量矩阵的研究[J]. 电子与信息学报, 2015, 37(6): 1317-1322. doi: 10.11999/JEIT140860.

ZHAO Ruizhen, WANG Ruoqian, ZHANG Fengzhen,. Research on the blocked ordered vandermonde matrix used as measurement matrix for compressed sensing[J].&, 2015, 37(6): 1317-1322. doi: 10.11999/JEIT140860.

[11] ZENG L, ZHANG X, CHEN L,. Deterministic construction of toeplitzed structurally chaotic matrix for compressed sensing[J].,,, 2015, 34(3): 797-813. doi: 10.1007/s00034-014- 9873-7.

[12] LI S and GE G. Deterministic sensing matrices arising from near orthogonal systems[J]., 2014, 60(4): 2291-2302. doi: 10.1109/ TIT.2014.2303973.

[13] MOHADES M M, MOHADES A, and TADAION A. A reed-solomon code based measurement matrix with small coherence[J]., 2014, 21(7): 839-843. doi: 10.1109/LSP.2014.2314281.

[14] YU N Y and GONG G. A new binary sequence family with low correlation and large size[J]., 2006, 52(4): 1624-1636. doi: 10.1109/ TIT.2006.871062.

[15] CHEN S S, DONOHO D L, and SAUNDERS M A. Atomic decomposition by basis pursuit[J]., 1998, 20(1): 33-61. doi: 10.1137/ S1064827596304010.

[16] TROPP J. Greed is good: algorithmic results for sparse approximation[J]., 2004, 50(10): 2231-2242. doi: 10.1109/TIT.2004.834793.

[17] DONOHO D L and ELAD M. Optimally sparse representation in general (nonorthogonal) dictionaries via1minimization[J]., 2003, 100(5): 2197-2202. doi: 10.1073/pnas. 0437847100.

[18] HAUPT J, BAJWA W U, RAZ G,. Toeplitz compressed sensing matrices with applications to sparse channel estimation[J]., 2010, 56(11): 5862-5875. doi: 10.1109/TIT.2010.2070191.

Construction of Compressed Sensing Measurement Matrix Based on Binary Sequence Family

LU Cunbo XIAO Song QUAN Lei

(,,’710071,)

It is significant to construct deterministic measurement matrix for the promotion and application of the Compressed Sensing (CS) theory. Originating from the algebraic coding theory, a construction algorithm of Binary Sequence Family (BSF) based deterministic measurement matrix is presented. The coherence is an important criterion to describe the property of matrices. Lower coherence leads to higher reconstruction performance. The coherence of the proposed measurement matrix is derived to be smaller than the corresponding Gaussian random matrix and Bernoulli random matrix. Theoretical analysis and simulation results show that the proposed matrix can obtain better reconstruction results than the corresponding Gaussian random matrix and Bernoulli random matrix. The proposed matrix can make the hardware realization convenient and easy by means of Linear Feedback Shift Register (LFSR) structures, thus being conductive to practical compressed sensing.

Signal processing; Compressed Sensing (CS); Measurement matrix; Binary Sequence Family (BSF)

TN911.72

A

1009-5896(2016)07-1682-07

10.11999/JEIT151076

2015-09-21；改回日期：2016-01-20；网络出版：2016-03-25

芦存博 444180647@qq.com

国家自然科学基金(61372069)，高等学校学科创新引智计划(111计划)(B08038)

The National Natural Science Foundation of China (61372069), The Programme of Introducing Talents of Discipline to Universities (111 Project) (B08038)

芦存博： 男，1989年生，博士生，研究方向为无线网络编码、压缩感知加密算法.

肖 嵩： 女，1977年生，教授，博士生导师，研究方向为网络编码、视频/图像联合信源信道编码.

权 磊： 男，1989年生，博士生，研究方向为无线传感器网络、压缩感知.