张　彦　　　　　　　韩张琴

(江苏省扬州市育才中学,225200)　(江苏省扬州市第一中学,225200)



旋转变换在平面几何中的应用

张彦韩张琴

(江苏省扬州市育才中学,225200)(江苏省扬州市第一中学,225200)

在解析几何中,我们学过从坐标系xOy到坐标系x′Oy′的变换:

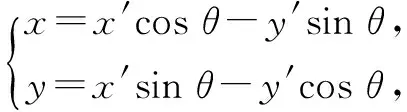
称之为旋转变换,用它来化简二次曲线方程甚为有效.这种变换在平面几何中也常用到,图形的旋转在初中八年级上册进行了介绍,学生基本都能掌握旋转的相关性质,但对于图形具有等边特性的平面几何问题,学生并不习惯利用图形的旋转来解题.事实上,下列问题可以考虑用旋转变换来改变元素的位置,将分散的条件集中起来,从而达到优解、巧解之目的.

例1设P是等腰三角形ABC内一点,AB=AC，且∠APB=∠APC，求证:PB=PC.

证明将∆APB沿着点A逆时针旋转,使得AB边与AC边重合,得到∆AP′C(如图1).

通过旋转,可得AP=AP′,BP=CP′, ∠APB=∠AP′C.

∵∠APB=∠APC,∠APB=∠AP′C，

∴∠APC=∠AP′C.

∵AP=AP′，∴∠APP′=∠AP′P，

∴∠CPP′=∠CP′P，∴CP=CP′.

又BP=CP′,∴PB=PC.

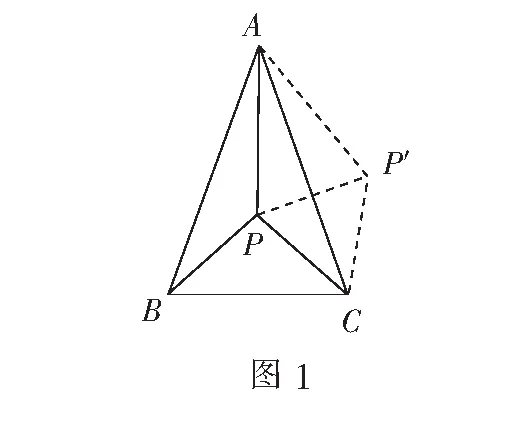
变式1如图2,已知等腰直角三角形ABC内有一点P,满足PA=1,PB=2,PC=3.求证:∠APB=135°.

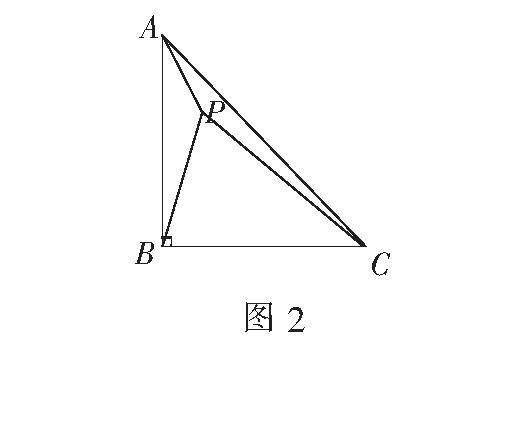
证明将∆APB沿着点B顺时针旋转90°,得到∆BP′C,并连结PP′(如图3).

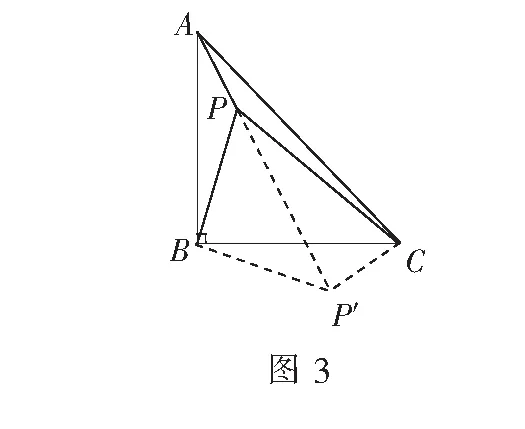
通过旋转,可得∠PBP′=90°,∠APB=∠CP′B,BP=BP′=2,P′C=AP=1.

∵∠PBP′=90°,且BP=BP′=2,

∴∆PBP′是等腰直角三角形，

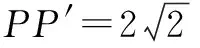
又在∆PP′C中,

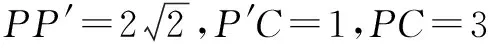
故有(PP′)2+(P′C)2=PC2，

∴∆PP′C是直角三角形,

∴∠PP′C=90°.

∴∠BP′C=∠PP′B+∠PP′C

=45°+90°=135°,

∴∠APB=∠BP′C=135°.

变式2如图4,等边三角形ABC内有一点P,满足PA=3,PB=4,PC=5,求证:∠APB=150°.

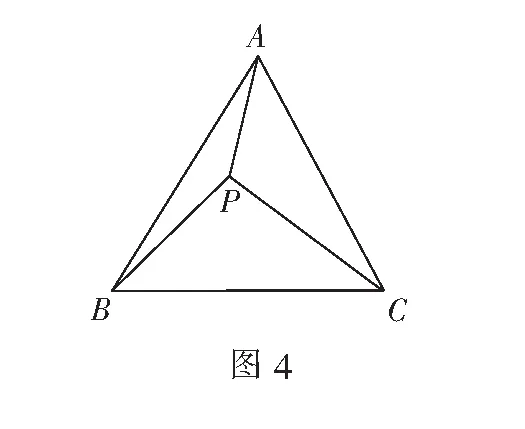
证明将∆APC沿着点A逆时针旋转60°,得到∆AP′B,并连结PP′(如图5).

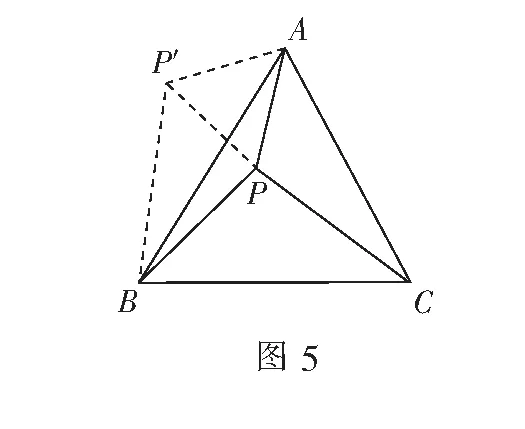
通过旋转,可得∠PAP′=60°,AP=AP′=3,P′B=PC=5.

∵∠PAP′=60°,AP=AP′=3,

∴∆PAP′是等边三角形，

∴∠APP′=60°,PP′=3.

又在∆PP′B中,

PP′=3,PB=4,P′B=5，

故有(PP′)2+(PB)2=P′B2，

∴∆PP′B是直角三角形,

∠P′PB=90°,

∴∠APB=∠APP′+∠PP′B

=60°+90°=150°.

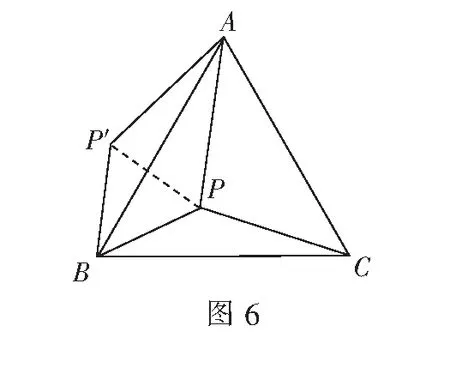
例2P是正三角形ABC内一点,连PA,PB,PC,若PA=10,PB=6,PC=8,求正三角形ABC的边长.

解如图6，将∆BPC绕点B逆时针旋转60°至∆BP′A位置，连结PP′,显然∆BPP′为正三角形.

在∆APP′中,AP=10,AP′=8,PP′=PB=6,则有

AP2=AP′2+PP′2,故∆APP′为直角三角形,∠AP′P=90°.

在∆ABP′中,

AB2=AP′2+BP′2-2AP′·

BP′cos∠AP′B，

即AB2=62+82-2×6×8cos 150°

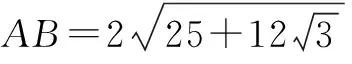
评注(1)若PA,PB,PC不为直角三角形三边,即∆APP′不为直角三角形时,上述方法仍适用,只须用余弦定理在∆PP′A中求出∠PP′A.

(2)将题中正三角形条件去掉,换成任意三角形亦可用上述方法求得.

变式P为正三角形ABC内一点,P到三个顶点A,B,C的距离分别为a,b,c.求证:

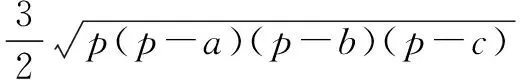
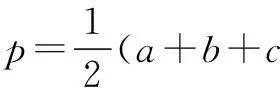
评注可以先求∆ABC的边长，也可分别将∆PAB、∆PBC、∆PCA仿上例的办法旋转可得三个小正三角形(边长分别为a,b,c)和三个全等的三边长为a,b,c的三角形.

最后,我们再来看一个由极值问题引发的结论.

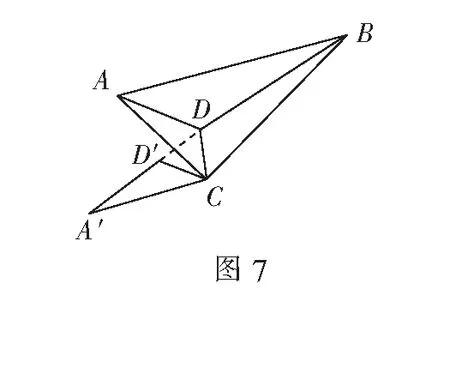
解设法将DA+DB+DC化为一条线段,为此将∆DCA绕C逆时针旋转60°至∆D′CA′位置(如图7)，则有

A′D′=AD,D′C=DC,∠D′CD=60°，

故∆CDD′为正三角形，D′D=DC.

于是DA+DB+DC=A′D′+D′D+DB，

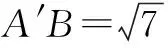
在∆A′CB中,A′B2=A′C2+BC2-2A′C·BCcos(90°+60°).

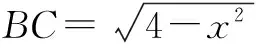
代入上式，有

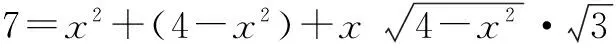
即x4-4x2+3=0，

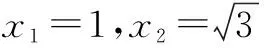
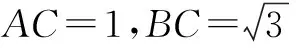
故∠A=60°或∠A=30°，

从而∠B=30°或60°.

评注(1)本题可将直角三角形的条件改成任意三角形,仿上不难求得三角形内到三顶点距离之和最小的点为该点至三角形三顶点连线夹角均为120°的点.

(2)再稍拓广便是著名的史坦豪斯“三村办学问题”.

当然,上述问题我们亦可以用平面几何的常规方法和解析几何的方法来处理.本文旨在说明旋转变换在解决此类问题的妙用,在平时的学习和研究中我们应适当加以关注.