刘世红，黄卓红，苏 翃

(1．四川工程职业技术学院基础教学部，四川德阳618000; 2．重庆理工大学数学与统计学院，重庆400054)

鞍点问题中的位移分裂预条件技术

刘世红1，黄卓红2，苏 翃2

(1．四川工程职业技术学院基础教学部，四川德阳618000; 2．重庆理工大学数学与统计学院，重庆400054)

提出一类位移分裂预条件技术(SSP)，用于求解大型稀疏非正定鞍点方程组，其中该方程组的系数矩阵具有非对称正定的(1，1)子块，同时，对于任意迭代参数α＞0，证明这一类位移分裂迭代法是无条件收敛的，最后通过数值算例进一步验证这类预条件技术的有效性和稳定性．

鞍点问题;位移分裂迭代法;预处理技术;Krylov子空间方法;无条件收敛

考虑如下具有2×2块结构的大型稀疏非对称鞍点问题Ax=b，即

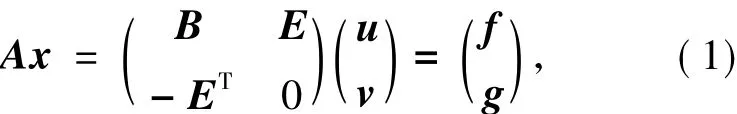
其中，B∈Rn×n是非对称正定的()是

对称正定的)，E∈Rn×m(n≥m)具有行满秩(即Rank(E)=m)，u，f∈Rn以及v，g∈Rm．本文使用(·)T和(·)*分别表示某矩阵或向量的转置和共轭转置．

鞍点问题(1)是一类特殊的增广线性系统．文献［1］对这类问题进行了详细的综述，认为这类问题广泛应用于科学计算和工程技术中，如带约束条件的优化问题、内点问题、最小二乘问题、计算流体力学、不可压缩性流体问题、结构分析以及无网格方法等．

当问题(1)中的系数矩阵A是大型稀疏不定矩阵时，采用直接求解方法不仅要计算(1，1)块子矩阵B的逆还需要计算B的Schur补ETB－1E的逆，求这些矩阵逆往往需要花费昂贵的求解代价，例如求解时间以及存储空间等．因此，迭代求解方法受到了研究人员的广泛关注，特别是使用高效迭代算法以及新型预条件技术对Krylov子空间方法进行预处理，已经成为求解大型稀疏鞍点问题的重要手段．

近几十年以来，为了更有效地求解大型稀疏线性系统，许多高效迭代算法和新型预条件技术已经被提出来，例如，埃尔米特和反埃尔米特分裂迭代方法(HSS)［2－3］、块对角及块三角预处理技术［4］、Uzawa类迭代算法［5］、超松弛迭代法(SOR)［6］、约束预处理技术［7］、位移分裂迭代法(SSP)以及广义位移分裂迭代法(GSSP)［8－13］．

为了更有效地求解非埃尔米特正定鞍点系统，文献［8］首先提出位移分裂迭代法思想，并且基于如下的矩阵分裂形式

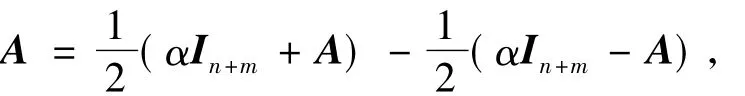
他们提出了如下形式的位移分裂预条件子

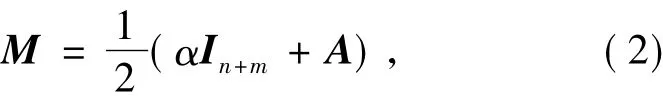
这里正常数α为迭代参数，而In+m表示n+m阶单位矩阵．

根据上述位移分裂思想，文献［9－10］同时提出了一类具有如下形式的广义位移分裂方法

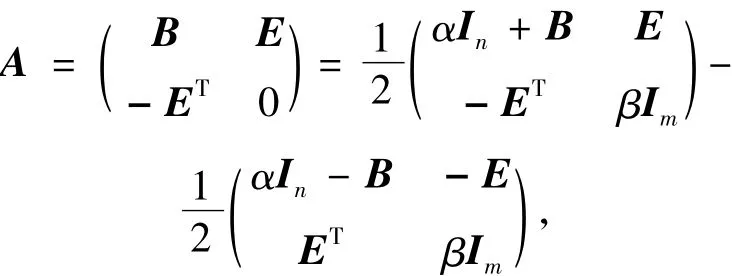
并给出了如下形式的广义位移分裂预条件子

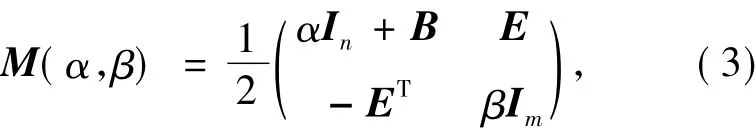
其中正常数α和β为迭代参数．

特别地，当迭代参数α=β时，文献［11］提出了位移分裂迭代法，并给出了如下形式的位移分裂预条件子

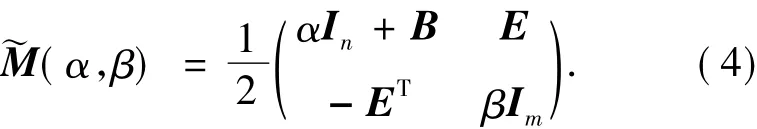
文献［12］应用广义位移分裂迭代法求解了大型稀疏鞍点问题(1)．根据文献［8－13］中的理论分析，可以很容易看出，无论迭代参数α和β取什么值，当位移迭代算法和广义位移迭代算法被应用于求解大规模稀疏鞍点问题时，它们都是无条件收敛的．

针对鞍点问题(1)的特殊结构，为了获得更有效的近似解，本文采用文献［13］中提出的理论验证方法，对文献［12］中的理论推导进行了简化，提出了较为简单的验证方法;同时，令迭代参数α=β，提出了一般的位移分裂迭代方法，通过理论分析，证明了位移分裂迭代法是无条件收敛的;最后，给出了数值算例来验证广义位移分裂预条件子的有效性和实用性．

1 位移分裂迭代法的收敛性分析

文献［12］应用广义位移分裂迭代法求解了大型稀疏鞍点问题(1)，提出了如下形式的预条件子

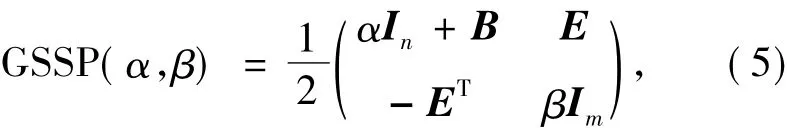
并且给出了如下形式的广义位移分裂迭代矩阵

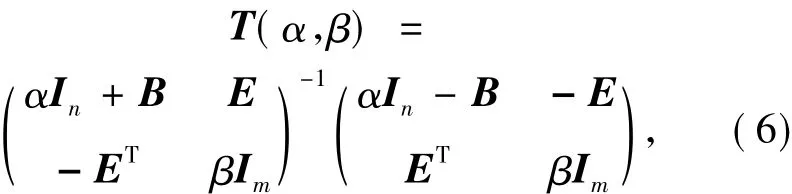
其中，B是非对称正定的，E具有行满秩正常数，而α和β为正常数．通过详细的理论分析，他们证明了这类广义位移分裂迭代方法无条件地收敛到鞍点问题(1)的唯一解．

本文根据文献［12］中提出的广义位移分裂预条件子(5)，提出了如下形式的预条件子

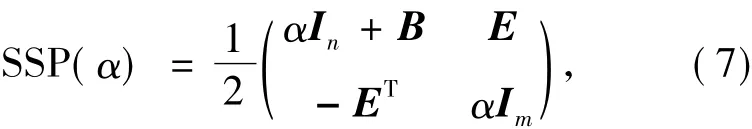
并且给出了如下形式的位移分裂迭代矩阵

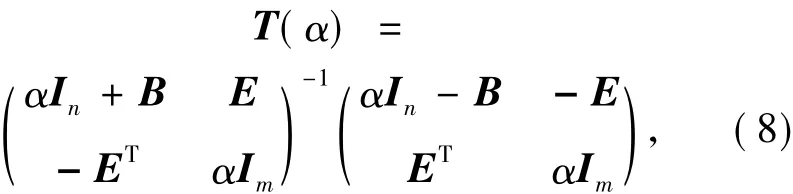
其中，B是非对称正定的，E具有行满秩正常数，而α为正常数．

采用文献［13］中提出的理论验证方法，使用一种比文献［14］提出的更加简单的方法来证明这类广义位移分裂迭代法无条件地收敛到鞍点问题(1)的唯一解，并且验证了本文提出的位移分裂迭代方法也是无条件收敛的．

记ρ(T)和 λ分别为迭代矩阵 T(α，β)(或T(α))的谱半径和任一特征值，设(u*，v*)*为对应于特征值λ的特征向量．根据文献［14］中提出的分裂迭代法的收敛性理论可知，(广义)位移分裂迭代法收敛的充要条件是ρ(T)＜1．考虑如下广义特征值问题

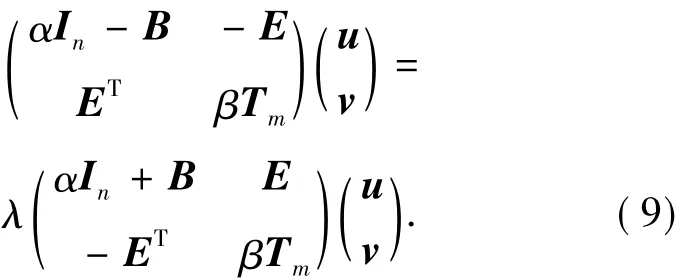
方程(9)等价为

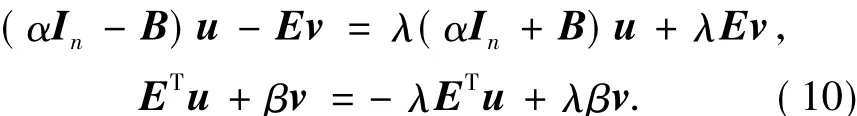
引理1．1 设B是非对称正定的，E具有行满秩，α和β是任意给出的正常数．另外假设λ是广义位移分裂迭代矩阵T(α，β)的任一特征值，则λ≠±1．

证明 假设(u*，v*)*是相应于特征值λ的特征向量．采用类似于文献［11］中的证明方式，如果λ=1，根据(10)式，可以得到如下结论

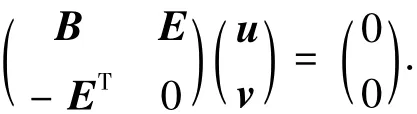
因为系数矩阵A是非奇异的［1］，因此，u=0且v=0．然而(u*，v*)*是相应于特征值λ的特征向量，显然u和v不可能同时为零，从而λ≠1．

同理可证λ≠－1．从而引理得证．

定理1．1 设B是非对称正定的，E具有行满秩，α和β是任意给出的正常数．记ρ(T)是迭代矩阵T(α，β)的谱半径，则ρ(τ(α，β))＜1，即广义位移分裂迭代法无条件地收敛到鞍点问题(1)的唯一解．

证明 由引理1．1可得 λ≠ ±1．为了证明ρ(τ(α，β))＜1，这里需要考虑如下2种情形．

(i)若0≠u∈N(ET)，根据方程(10)中的第一个方程，可以得到

设u*Bu=a+bi，因为B是正定的，显然a＞0，因此，下列不等式成立

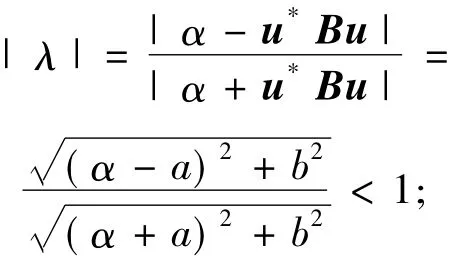
(ii)若u∉N(ET)，不失一般性，假设‖u‖2= 1，使用类似于文献［13］中的理论验证方法，在方程(10)的第一个及第二个方程中分别乘以向量u*及v*，并且对第二个方程进行共轭转置，从而获得如下结论

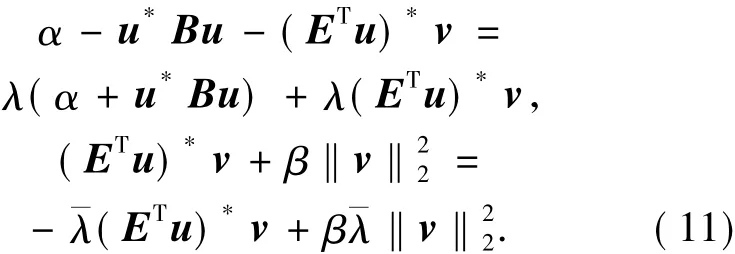
由方程(11)中的第二个方程可得

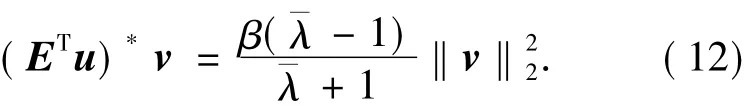
将方程(12)代入(11)式中的第一个方程，则有

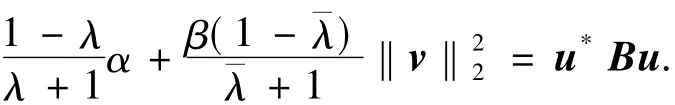
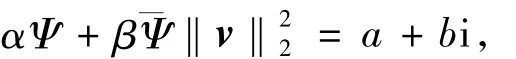
进一步，可以计算出Ψ的实部

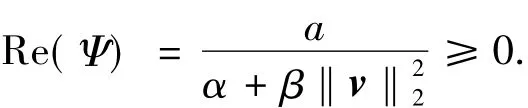
因此，可以获得位移分裂迭代矩阵的特征值满足如下不等式

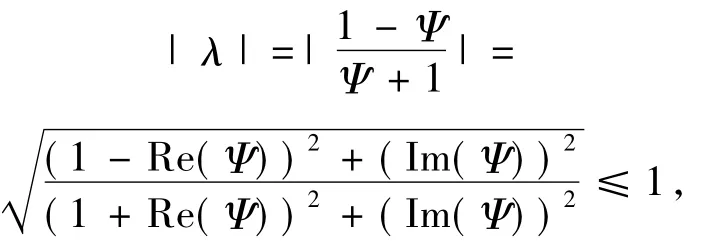
这里使用Re(Ψ)和Im(Ψ)分别表示Ψ的实部及虚部，即

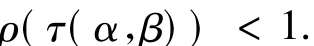
因此，广义位移分裂迭代法无条件地收敛到鞍点问题(1)的唯一解．

从而，定理得证．

接下来，考虑如下形式的位移分裂迭代法．给定初始向量x0，计算

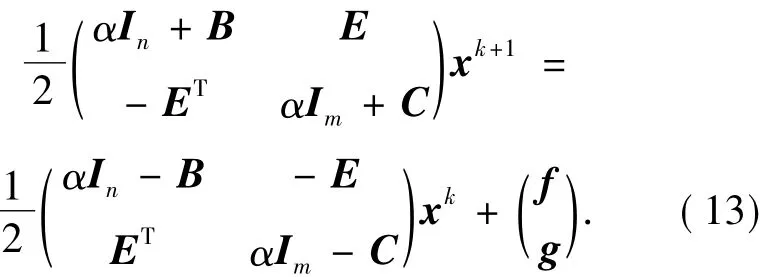
直到迭代序列xk(k=0，1，2，…)收敛到给定精度，则迭代终止．

在方程(9)和(10)中令α=β，则可以获得如下形式的广义特征值问题

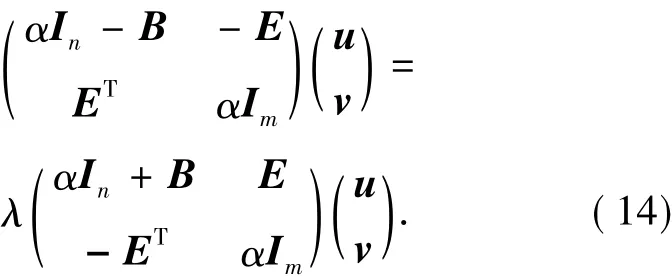
方程(14)等价为

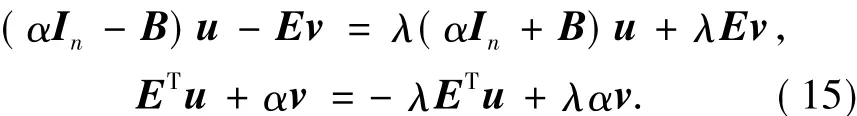
定理1．2 设B是非对称正定的，E具有行满秩，α是任意给出的正常数．记ρ(T)是迭代矩阵T(α)的谱半径，则ρ(τ(α))＜1，即位移分裂迭代法无条件地收敛到鞍点问题(1)的唯一解．

证明 根据引理1．1，则 λ≠ ±1．为了证明ρ(τ(α))＜1，这里仅需要考虑如下2种情形．

(i)若0≠u∈N(ET)，根据方程(15)中的第一个方程有

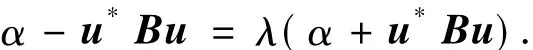
设u*Bu=a+bi，因为B是正定的，那么a＞0，因此，下列不等式成立

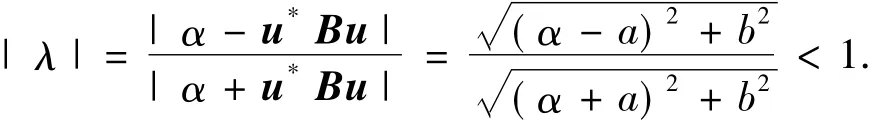
(ii)若u∉N(ET)，不失一般性，假设‖u‖2= 1，使用类似于文献［13］中的理论验证方法，在方程(15)的第一个及第二个方程中分别乘以向量u*及v*，从而获得如下结论

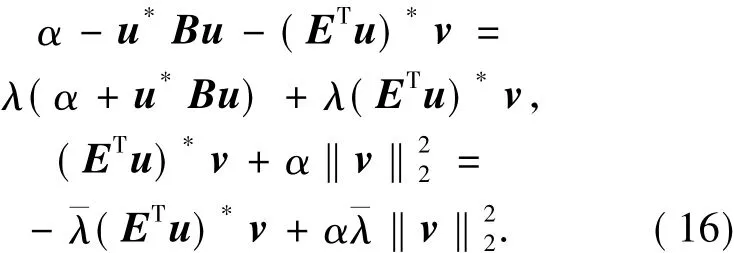
对方程(16)中的第二个方程进行变形，可以获得如下形式的等式

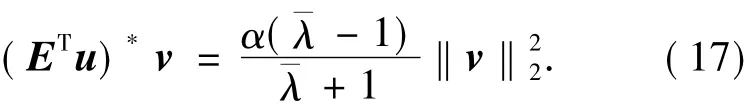
将方程(17)代入方程(16)中的第一个等式可得

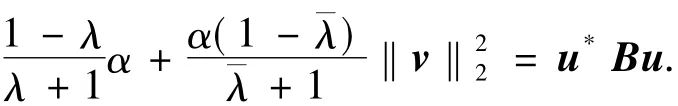
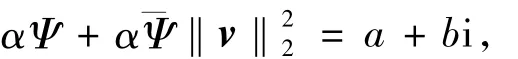
进一步，可以计算出Ψ的实部

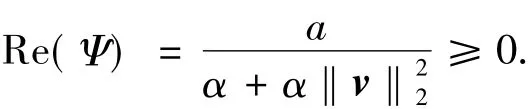
因此，可以获得位移分裂迭代矩阵的特征值满足如下不等式

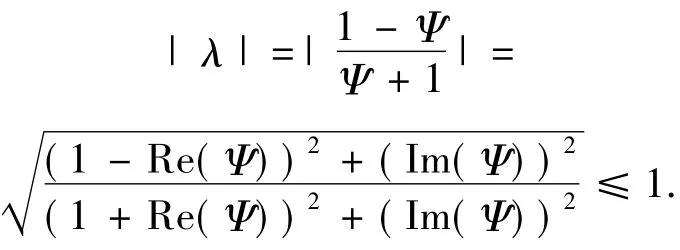
这里使用Re(Ψ)和Im(Ψ)分别表示Ψ的实部及虚部．因为λ≠±1，所以ρ(τ(α))＜1．

因此，位移分裂迭代法无条件地收敛到鞍点问题(1)的唯一解．从而，定理得证．

2 数值实验

下面将给出一个数值例子来进一步研究我们的理论分析并验证本文提出的位移分裂预条件子的实用性及可行性．通过使用位移分裂预条件子SSP(α)及预条件子HSS预处理重启的GMRES［15］迭代方法，将两类预条件子SSP(α)及HSS进行了数值比较，这里HSS(α)预条件子定义为

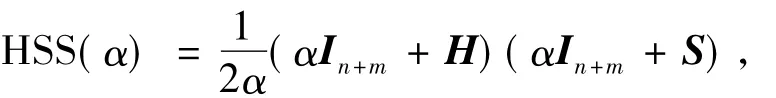
其中

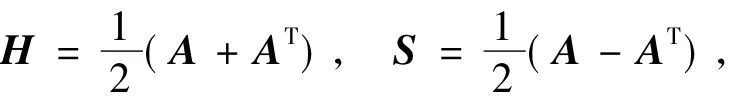
这里A是定义在问题(1)中的系数矩阵．

使用“IT”和“CPU”分别表示迭代所需迭代步数和计算时间(以秒记)．在计算中，选用零向量作为初始迭代向量，即u0=(0，0，…，0)，对于具体问题如果迭代次数超过1 000次或者第k步相对误差满足

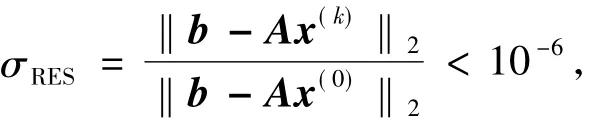
则终止迭代过程．

例2．1 考虑如下Oseen方程

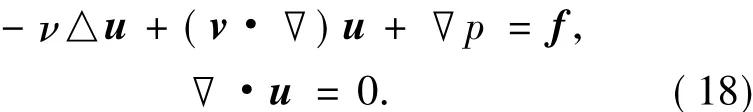
在这个数值实验中，使用H．C．Elman等［16］开发的“IFISS”软件包中的Q2－Q1有限元方法离散Oseen方程中的二维“lid－driven cavity”问题．在实际计算过程中，这里黏性系数ν=0．1，通常选择16× 16、32×32以及64×64的四边形一致网格来离散问题区域Ω．

在实际计算中，采用16×16、32×32、64×64及128×128的均匀网格来离散问题域Ω．表1(α= 0．01和υ=0．001)和表2(α=0．002和υ=0．01)中，对重启数取为20的广义极小残量方法进行预处理，将本文提出的SSP方法和文献［3］中的HSS方法进行了数值比较．从这2个表格中的数据可以看出:无论从迭代数还是求解时间方面，SSP方法要略优于文献［3］中的HSS方法．但要从理论上验证SSP方法优于HSS方法以及确定SSP预条件子的最优迭代参数仍需要进一步研究．

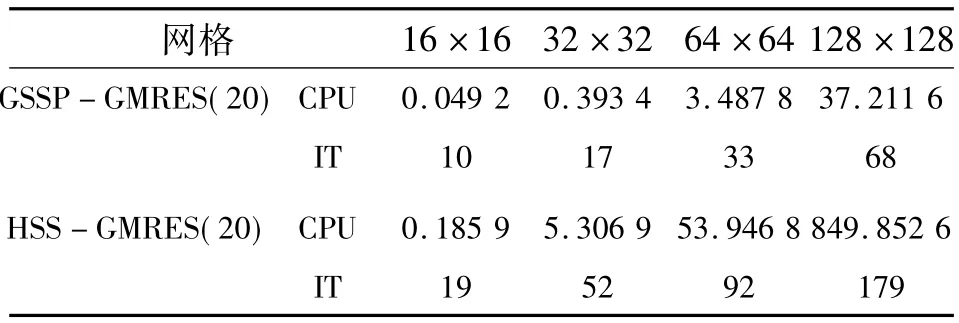
表1 迭代步数及计算时间Table 1 Number of iterations and solution time in seconds

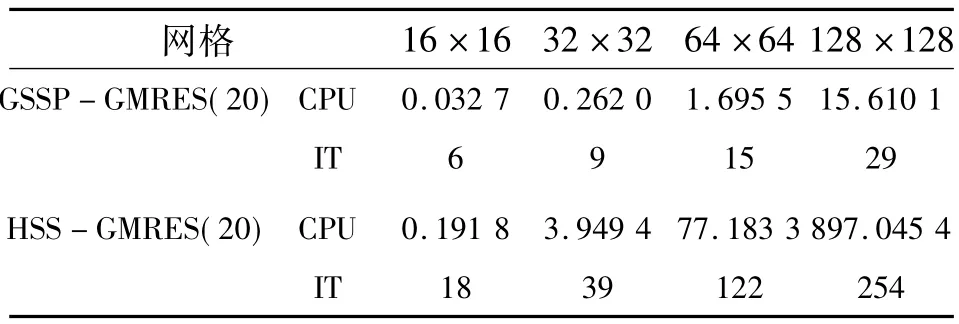
表2 迭代步数及计算时间Table 2 Number of iterations and solution time in seconds

［1］BENZI M，GOLUB G H，LIESEN J．Numerical solution of saddle point problems［J］．Acta Numer，2005，14:1－137．

［2］BAI Z Z．Optimal parameters in the HSS－like methods for saddle－point problems［J］．Numer Linear Algebra Appl，2009，16: 447－479．

［3］BENZI M，GOLUB G H．A preconditioner for generalized saddle point problems［J］．SIAM J Matrix Anal Appl，2004，26:20－41．

［4］BAI Z Z，CHAN R H，REN Z R．On order－reducible sinc discretizations and block－diagonal preconditioning methods for linear third－order differential equations［J］．Numer Linear Algebra Appl，2014，21:108－135．

［5］CHEN P Y，HUANG J G，SHENG H S．Some Uzawa methods for steady incompressible Navier－Stokes equations discretized by mixed element methods［J］．J Comput Appl Math，2015，273:313－325．

［6］雷刚．预处理(I+S)后改进的SOR迭代法收敛性讨论［J］．四川师范大学学报(自然科学版)，2011，34(4):528－531．

［7］BERGAMASCHI L．On eigenvalue distribution of constraint－preconditioned symmetric saddle point matrices［J］．Numer Linear Algebra Appl，2012，19:754－772．

［8］BAI Z Z，YIN J F，SU Y F．Shift－splitting preconditioner for non－Hermitian positive definite matrices［J］．J Comput Math，2006，24:539－552．

［9］曹阳，陶怀仁．鞍点问题的广义位移分裂预条件子［J］．计算数学，2014，36:16－26．

［10］CHEN C R，MA C F．A generalized shift－splitting preconditioner for saddle point problems［J］．Appl Math Lett，2015，43:49－55．

［11］CAO Y，DU J，NIU Q．Shift－splitting preconditioners for saddle point problems［J］．J Comput Appl Math，2014，272:239－250．

［12］CAO Y，LI S，YAO L Q．A class of generalized shift－splitting preconditioners for nonsymmetric saddle point problems［J］．Appl Math Lett，2015，49:20－27．

［13］SALKUYEH D K，MASOUDI M，HEZARI D．On the generalized shift－splitting preconditioner for saddle point problems［J］．Appl Math Lett，2015，48:55－61．

［14］YOUNG D M．Iterative Solution of Large Linear Systems［M］．New York:Academic Press，1971．

［15］SAAD Y，SCHULTZ M H．GMRES:a generalized minimal residual algorithm for solving nonsymmetric linear systems［J］．SIAM J Sci Statist Comput，1986，7:856－869．

［16］ELMAN H C，RAMAGE A，SILVESTER D J．IFISS:a Matlab toolbox for modelling incompressible flow［J］．ACM Trans Math Software，2007，33:Article14．

［17］于善玲，张耀明．二维Helmholtz方程的边界元法［J］．重庆理工大学学报(自然科学版)，2015，29(11):139－143．

On the Shift-splitting Preconditioning Technique for the Saddle Point Problems

LIU Shihong1，HUANG Zhuohong2，SU Hong2

(1．Department of General Studies，Sichuan Engineering Technical College，Deyang 618000，Sichuan; 2．School of Mathematics and Statistics，Chongqing University of Technology，Chongqing 400054)

In this paper，the shift-splitting iteration method is used to solve the large sparse indefinite saddle point systems with nonsymmetric positive definite(1，1)-block．It is analysed that the shift-splitting iteration method converges unconditionally to a unique solution of saddle point system for any iteration parameter α＞0．A numerical experiment shows the correctness and the feasibility of the shift-splitting iteration method．

saddle point problems;shift-splitting iteration method;preconditioning technique;Krylov subspace methods;unconditional convergence

O151．21

A

1001－8395(2016)04－0549－05

10．3969/j．issn．1001－8395．2016．04．016

(编辑 李德华)

2015－11－25

重庆市基础与前沿研究一般项目(CSTC2015JCYJAA1432)和重庆市教委科技项目(KJ1500941)

刘世红(1960—)，男，讲师，主要从事代数学、数值代数及其应用的研究，E－mail:lsh@scetc．edu．cn

2010 MSC:65F10