冯 琳，段复建

(1．重庆文理学院数学与财经学院，重庆永川402160; 2．桂林电子科技大学数学与计算科学学院，广西桂林541004)

一个自动确定信赖域半径的锥模型信赖域方法

冯 琳1，段复建2

(1．重庆文理学院数学与财经学院，重庆永川402160; 2．桂林电子科技大学数学与计算科学学院，广西桂林541004)

自适应信赖域算法由于利用了对算法有重大影响的有关当前迭代点的信息，提高了算法的效率，因此对于无约束最优化问题提出一个锥模型自适应信赖域算法．算法中信赖域半径采用新的自适应修正策略．算法在每步迭代中以R－函数变化的速率、水平向量信息以及当前迭代点的一阶导数信息来修正信赖域半径的大小，使得信赖域半径的修正依据于问题本身，克服传统信赖域算法中没有利用当前迭代点的信息修正信赖域半径的缺点．在一定的条件下简洁地给出了算法的全局收敛性分析．算法丰富了已有的自适应信赖域算法．

无约束最优化;信赖域方法;锥模型;自适应;全局收敛性

其中，f(x):Rn→R1是连续可微函数．本文采用如下记号:‖·‖表示Euclidean范数;g(x)∈Rn是f(x)在点x的梯度;H(x)∈Rn×n是f(x)在点x的Hessian矩阵，{xk}是某一算法产生的迭代点列，并记fk=f(xk)，gk=g(xk)，Hk=H(xk);Bk∈Rn×n是对称矩阵，它是f(x)在点xk的Hessian矩阵或其近似．

信赖域算法和线搜索方法是求解(1)式的两类主要的数值计算方法．与线搜索方法相比，信赖域算法具有稳定的数值性能、收敛性强、迭代次数少、能有效地解决病态问题，并且不需要子问题的Hessian矩阵是正定的．因此在非线性优化界受到了特别的重视，特别是最近几年一直是非线性优化界研究的一个热点．

信赖域算法是一种迭代算法．在每一步迭代，求解信赖域子问题

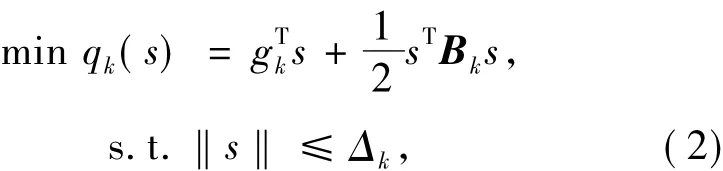
本文考虑无约束最优化问题

其中，s=x－xk，gk=f(xk)，Δk＞0是信赖域半径．

在当前迭代点xk，设子问题(2)的解是sk，则在点xk处的实际下降量

预估下降量

实际下降量Are sk与预估下降量Pre sk的比值为

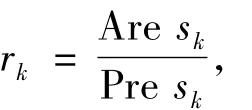
它反映了子问题(2)的解sk令人满意的程度．rk越大，表明sk越令人满意．如果sk令人满意，就接受sk，得到下一个迭代点xk+1，同时增大信赖域半径Δk;反之，则拒绝sk，同时缩小信赖域半径Δk，重新求解子问题(2)，直至sk被接受，即

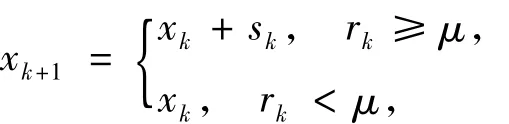
其中，μ∈(0，1)是一个常数，并调节信赖域半径

其中，0≤μ1＜μ2＜1，0＜c1＜1＜c2是常数．

(3)式表明对信赖域半径Δk的调节只是根据rk按常数倍放大或缩小初始信赖域半径，没有利用对算法有重大影响的gk、Bk等这些有关当前迭代点的信息，这样降低了算法的效率．基于此，许多自适应信赖域方法被提出．A．Sartenaer［1］研究了初始信赖域半径的选取对信赖域算法的影响，提出一个自动确定初始信赖域半径的ITRR方法．J．Y．Fan等［2］提出信赖域半径收敛到零的方法，其信赖域半径Δk=μk‖gk‖．李红等［3］提出一个充分利用rk的信息，利用R－函数变化的速率自动确定信赖域半径Δk=Rη(t)‖dk－1‖的方法，其中Rη(t)是一个关于rk的R－函数．文献［4－6］也提出了自适应信赖域方法．

定义1［7］Rη(t)定义在(－∞，+∞)上，参数η∈(0，1)，Rη(t)是一个R－函数当且仅当满足:

(i)Rη(t)在(－∞，+∞)非减;

(iii)Rη(t)≤1－γ1(t＜η，γ1∈(0，1－β)是一个常数);

(iv)Rη(η)=1+γ2(γ2∈(0，β)是一个常数);

由定义1得到R－函数如下一些性质．

定理1［7］如果Rη(t)(η∈(0，1))是一个R－函数，则有

因此可以把Rμ(rk)作为增大或缩小信赖域半径的尺度，使信赖域半径的调节依据于问题本身．

大多数信赖域算法采用二次模型逼近原问题f(x)，但对一些非二次性态强、曲率变化剧烈的函数，采用二次模型逼近原问题效果较差，因此得到的最优点较差．W．C．Davidon［8］首次提出锥模型．锥模型比二次模型更一般，包含的信息和自由度更多，更能充分地逼近原问题f(x)，因而吸引了许多学者对它进行研究．文献［9－11］研究了锥模型共线调比拟牛顿方法．诸梅芳等［12］提出求解(1)的锥模型信赖域算法;Q．Ni［13］给出锥模型信赖域子问题的最优性条件，为锥模型信赖域子问题的求解提供了更充分、合理的理论基础，信赖域算法进一步发展．文献［14－16］提出了锥模型非单调信赖域算法．文献［17］提出了锥模型回溯过渡信赖域算法．J．H．Fu等［18］将自适应技术引入锥模型信赖域算法，提出锥模型自适应信赖域算法［19－25］;王希云等［26］也提出锥模型自适应信赖域算法，信赖域半径

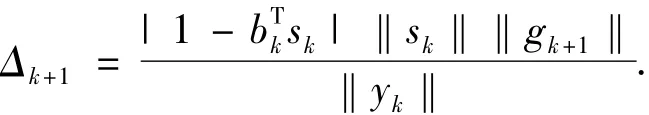
锥模型信赖域算法得到了广泛的发展，并且数值结果表明对一些函数，特别是对曲率变化剧烈的函数，锥模型信赖域算法比二次模型信赖域算法效果更好．

求解(1)式的一个典型的锥模型信赖域子问题是

其中，bk∈Rn是水平向量，．当bk=0或时，锥模型转化为二次模型，因此锥模型是二次模型的推广．

在文献［2－3，26］工作的基础上，基于锥模型信赖域子问题(6)，本文提出一类新的自动确定信赖域半径的信赖域方法．每次迭代，令使得在每次迭代，依据问题本身的信息自动调节信赖域半径．

1 自动确定信赖域半径的锥模型信赖域方法

基于锥模型信赖域子问题(6)和新的信赖域半径(7)，给出一个求解(1)式的自适应信赖域方法．

设(6)式的解为sk，则目标函数f(x)在第k步的实际下降量为

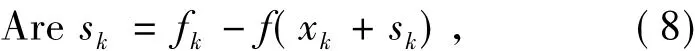
预估下降量为

比值

具体的自动确定信赖域半径的锥模型信赖域方法实现如下．

算法1 第1步 给出初始点x0∈Rn，Δ0＞0，b0∈Rn×1，ε＞0，0＜μ＜1，0＜β＜1，0＜γ1＜1－β，γ2＞0，M＞1+γ2，B0=I(单位阵)，k:=0．

第2步 计算gk=g(xk)．如果‖gk‖≤ε，则停止计算，x*=xk;否则，转第3步．

第3步 近似求解(6)式得到sk，并利用(8)～(10)式分别计算Are sk、Pre sk、rk．

第4步 如果rk＜μ，令xk+1=xk;否则，令xk+1=xk+sk．

第5步 修正bk及Bk，产生bk+1及Bk+1，利用(7)式计算Δk+1．令k:=k+1，转第2步．

注1．1 (i)算法1中，要求‖bk‖Δk＜1，如果‖bk‖Δ≥1，则令，使得‖bk‖Δk＜1．

(ii)算法1第3步中sk的具体求解及第5步中bk和Bk的校正公式可参见文献［18］．

(iii)若(6)和(7)式中的bk=0，则算法1转化为相应的自动确定信赖域半径的二次模型信赖域方法．

(iv)算法1中，利用(3)式调节信赖域半径，得到传统的锥模型信赖域算法．

2 算法的收敛性

在一定的条件下证明算法1的全局收敛性．

本文所需假设如下:

(A1)水平集L(x0)={x|f(x)≤f(x0)}有界，f(x)在L(x0)上二阶连续可微;

(A2){Bk}、{}、{bk}一致有界，即存在常数δ1，δ2，δ3＞0，使得对k有‖Bk‖≤δ1，‖‖≤δ2，‖bk‖≤δ3;

(A3)g(x)是Lipschitz连续函数，即存在L＞0，满足

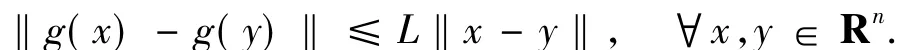
为讨论方便，记I={k:rk＜μ}，J={k:rk≥μ}．

引理1 设sk是子问题(6)的解，gk≠0，则有

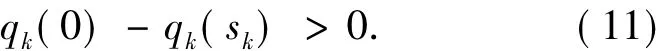
为得到算法的下降性条件，引入Cauchy点

其中

引理2 对Cauchy点pck满足

证明 分3种情况证明．

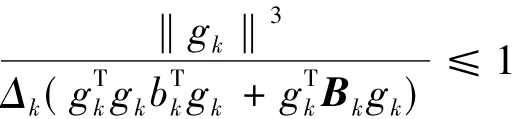
时

则有

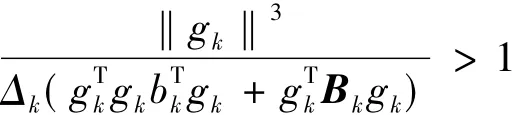
时3

由‖Bk‖Δk＜1知

则有

由(13)～(16)式知

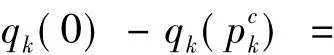
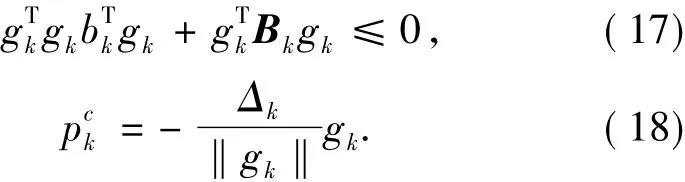
由(17)式知

于是

从而

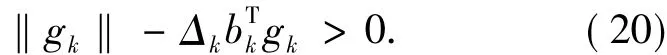
由(17)式知

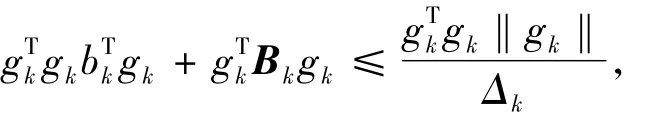
于是

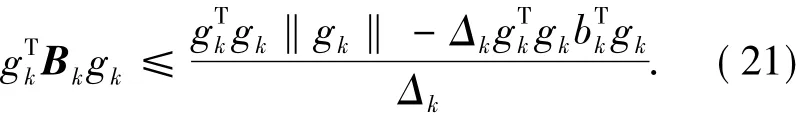
又

由(21)和(22)式知

于是由(18)、(23)式和(ii)的过程，(19)和

(20)式知

证毕．

下面的引理说明子问题(6)的解sk满足充分下降条件．

引理3 设sk是子问题(6)的解，则有

证明 由引理2知

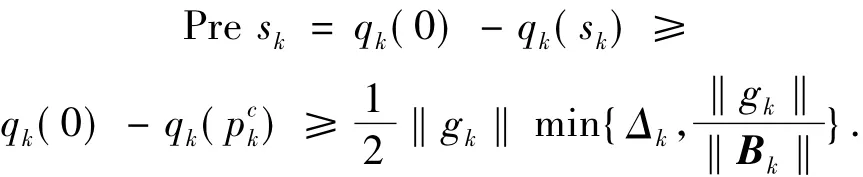
引理4 如果假设(A1)～(A3)成立，则存在常数c＞0，使得

证明 由(5)和(7)式及‖bk‖Δk＜1知

令c=2M，则Δk≤c‖gk‖，从而‖sk‖≤c‖gk‖．

引理5 如果{xk}是由算法1产生的点列，则

证明 用数学归纳法证明．

当k=0时，f(x0)≤f(x0)，则x0∈L(x0)，命题成立．

下证假设xk∈L(x0)时，则有xk+1∈L(x0)．

当xk∈L(x0)时，有f(xk)≤f(x0)．

(i)如果k∈I，则rk＜μ．

由算法1第4步知:xk+1=xk，于是 f(xk+1)= f(xk)．所以f(xk+1)≤f(x0)．

(ii)如果k∈J，则rk≥μ．于是由(11)式知

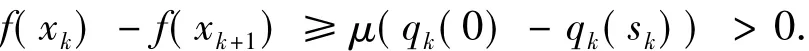
因而f(xk+1)≤f(xk)．所以f(xk+1)≤f(x0)．

由(i)和(ii)知:当xk∈L(x0)时，xk+1∈L(x0)．

由数学归纳法知:结论成立．

算法1中，如果xk+1=xk+sk，则称xk+1是一个成功的迭代点;如果xk+1=xk，则称xk+1是一个非成功的迭代点．

引理6 如果假设(A1)～(A3)成立，{xk}是由算法1产生的无穷点列，且对k有‖gk‖＞ε，ε∈(0，1)是常数，则对，存在非负整数p使得xk+p+1是一个成功的迭代点．

证明 假设存在非负整数 k0使得p都有xk0+p+1是一个非成功的迭代点，即

由算法1第4步知

由(4)和(7)式知

于是

因而对充分大的p有 1

其中c1为某一常数．

于是对充分大的p有

由(24)式知

由f(x)是连续可微函数及Taylor展开式知

其中

由于f(x)二阶连续可微，则对x∈{x|f(x)≤f(x0)，x∈Rn}，α＞0，s．t．‖2f(x)‖≤α．

由(29)～(31)式知

从而当p充分大时

由0＜μ＜1知:当p充分大时，rk0+p≥μ，这与(26)式矛盾．

定理2 如果假设(A1)～(A3)成立，算法1产生无穷点列{xk}，则有

证明 (反证法)假设结论不成立，则存在常数ε＞0，ε∈(0，1)，使得‖gk‖≥ε，k．

下证

由引理6知:当k充分大时，则k∈J，此时有

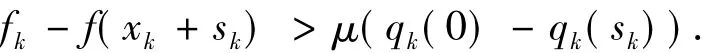
由于{fk}单调递减有下界，因此{fk}收敛．

于是当k充分大时有

因为‖bk‖Δk＜1;当‖bk‖Δ≥1，则(0＜α＜1)，因此τ＞0，使得‖bk‖Δk≤τ．于是

所以

由(34)式知

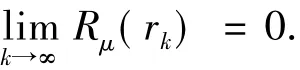
又k∈J时，有rk≥μ，由定义1和定理1知:，使得，这与(33)式矛盾．因此定理成立．

3 结论

对于无约束最优化问题提出了一个基于锥模型的自适应信赖域算法．信赖域半径采用一个新的自适应修正策略．算法在每步迭代中以R－函数变化的速率、水平向量信息以及当前迭代点的一阶导数信息来修正信赖域半径的大小，使得信赖域半径的修正依据于问题本身，克服了传统信赖域算法中没有利用当前迭代点的信息修正信赖域半径的缺点．在一定的条件下给出了新算法的全局收敛性分析．

致谢 重庆文理学院校级基金(Y2013SC42)对本文给予了资助，谨致谢意．

［1］SARTENAER A．Automatic determination of an initial trust region in nonlinear programming［J］．SIAM J Scientific Computing，1997，18:1788－1803．

［2］FAN J Y，AI W B，ZHANG Q Y．A line search and trust region algorithm with trust region radius convergence to zero［J］．J Comput Math，2004，22(6):865－872．

［3］李红，焦宝聪．一类带线搜索的自适应信赖域算法［J］．运筹学学报，2008，12(2):97－104．

［4］SANG Z Y，SUN Q Y．A self－adaptive trust region method with line search based on a simple subproblem model［J］．J Comput Appl Math，2009，232:514－522．

［5］冯琳，段复建．无约束优化的一个滤子非单调信赖域算法［J］．四川师范大学学报(自然科学版)，2015，38(2):223－229．

［6］朱帅，朱世昕，王希云．基于新锥模型的带固定步长的非单调自适应信赖域算法［J］．西南民族大学学报(自然科学版)，2012，38(1):44－49．

［7］HEI L．A self－adaptive trust region algorithm［J］．J Comput Math，2003，21:229－236．

［8］DAVIDON W C．Conic approximations and collinear scaling for optimizers［J］．SIAM J Numer Anal，1980，17(2):268－281．

［9］SORENSON D C．The Q－superlinear convergence of a collinear scaling algorithm for unconstrained optimization［J］．SIAM J Numer Anal，1980，17:84－114．

［10］ARIYAWANSA K A．Deriving collinear scaling algorithms as extension of quasi－Newton methods and the local convergence of DFP and BFGS－related collinear scaling algorithms［J］．Math Prog，1990，49:23－48．

［11］SHENG S．Interpolation by conic model for unconstrained optimization［J］．Computing，1995，54:83－98．

［12］诸梅芳，薛毅，张凤圣．锥模型的拟NEWTON型信赖域方法［J］．高等学校计算数学学报，1995，17(1):36－47．

［13］NI Q．Optimality conditions for trust－region subproblems involving a conic model［J］．SIAM J Optim，2005，15(3):826－837．

［14］QU S J，JIANG S D，ZHU Y．A conic trust－region method and its convergence properties［J］．Comput Math Appl，2009，57: 513－528．

［15］CUI Z C，WU B Y，QU S J．Combining nonmonotone conic trust region and line search techniques for unconstrained optimization［J］．J Comput Appl Math，2011，235:2432－2441．

［16］JI Y，LI Y J，ZHANG K C，et al．A new nonmonotone conic trust－region method of conic model for solving unconstrained optimization［J］．J Comput Appl Math，2010，233:1746－1754．

［17］葛恒武．无约束优化问题的锥模型回溯过滤信赖域算法［J］．苏州大学学报(自然科学版)，2010，26(2):8－15．

［18］FU J H，SUN W Y，RAIMUNDO J B De Sampaio．An adaptive approach of conic trust－region method for unconstrained optimization problems［J］．Appl Math Comput，2005，19(1/2):165－177．

［19］ZHANG J，ZHANG K，QU S．A nonmonotone adaptive trust region method for unconstrained optimization based on conic model［J］．Appl Math Comput，2010，217(8):4265－4273．

［20］孙文瑜，徐东．解无约束最优化的基于锥模型的过滤集－信赖域方法［J］．中国科学，2012，42(5):527－543．

［21］ZHAO L．Non－monotone adaptive filter conic trust region method for unconstrained optimization［J］．J Math Comput Sci，2012(6):1874－1893．

［22］李小伟，钱慧敏．带有线搜索的非单调自适应新锥模型信赖域算法［J］．电子科技，2013，26(11):4－6，46．

［23］ZHOU Q，ZHOU F，CAO F．A nonmonotone trust region method based on simple conic models for unconstrained optimization［J］．Appl Math Comput，2013，225(12):295－305．

［24］CUI Z．A nonmonotone adaptive trust region method based on conic model for unconstrained optimization［J］．J Optimization，2014，2014:1－8．

［25］ZHOU Q，ZHANG．An adaptive trust region method based on simple conic models［J］．J Math Modelling Algorithms in Operations Research，2015:1－15．

［26］王希云，王庆．一种基于新锥模型的自适应信赖域算法［J］．应用数学，2010，23(2):307－312．

A Trust Region Method with Automatic Determination of the Trust Region Radius Based on the Conic Model

FENG Lin1，DUAN Fujian2

(1．School of Mathematics and Finance，Chongqing College of Arts and Sciences，Yongchuan 402160，Chongqing; 2．School of Mathematics and Computational Science，Guilin University of Electronic Technology，Guilin 541004，Guangxi)

In this paper，we propose a self-adaptive trust region method based on the conic model for unconstrained optimization problems．The trust region radius is updated with a new self-adaptive strategy．At every iteration，the trust region radius is updated at the variable rate of R-function，the level vector information and the first order derivative information at the current point，thus the updation of the trust region radius is dependent of the problem itself，which overcomes the shortcoming，that the information at the current point in the traditional trust region algorithms is not applied．The global convergence of the new method is briefly analyzed under mild conditions．The method enriches the existing self-adaptive trust region methods．

unconstrained optimization;trust region method;conic model;self-adaptive;global convergence

O224．2

A

1001－8395(2016)04－0542－07

10．3969/j．issn．1001－8395．2016．04．015

(编辑 李德华)

2014－07－03

国家自然科学基金(11061011)和广西自然科学基金(2011GXNSFA018138)

冯 琳(1973—)，女，讲师，主要从事最优化理论与算法的研究，E－mail:fenglin730825@126．com

2010 MSC:90C30;65K10