吴 杉，余盛利，汪金汉

（1．湖北师范大学计算机科学学院，湖北黄石435002；2．湖北师范大学数学与统计学院，湖北黄石435002）

一个不等式的证明及其推广

吴 杉1，余盛利2，汪金汉2

（1．湖北师范大学计算机科学学院，湖北黄石435002；2．湖北师范大学数学与统计学院，湖北黄石435002）

对于高等数学教材数学分析中的一个不等式，用两种初等数学的方法给出了证明．将此不等式的右边变形后，又得到两个不等式，而且与普通高中课程《不等式选讲》［4］中的不等式建立联系，并对这些不等式做了六个推广．

对称性；排序不等式；推广

在高等数学教材数学分析［1］中，对于一个初等的幂不等式，是根据凸函数的性质，利用詹森（Jansen）不等式给出的证明．本文首先用两种简单的初等数学方法给出了该不等式证明；其次将此不等式的右边变形后，又得到两个不等式，其中把一个不等式与普通高中课程标准实验教科书．数学．不等式选讲［2］中的不等式建立联系；由于例1、例2、例3中三个不等式左边都相同，在判断它们右边幂的乘积式大小时，例4中的（3）（ii）借助于Mathematic5．0软件编程数据测试，而得到了一组数据．最后对这些不等式做了六个推广．

在数学分析［1］中给出了一个证明幂不等式的例题：

例1 设a，b，c∈ℝ＋，求证aabbcc≥（abc）

证法1（用詹森Jansen不等式） 设f（x）＝xlnx，x＞0．由f〃（x）＝＞0，（x＞0），知f（x）＝xlnx在x＞0时为严格凸函数，依詹森不等式有

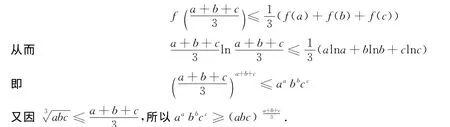
注：这里是高等数学中构造凸函数，利用函数的凸性，借助于詹森（Jansen）不等式和平均不等式得到证明．

下面给出两种初等数学的证明方法。

证法2（商值比较法） 由于不等式是关于a，b，c对称的，不妨设a≥b≥c＞0，则

注 该证法虽然非常简单，但变形的技巧很强．

证法3（用排序不等式） 由对称性，设a≥b≥c＞0，则lna≥lnb≥lnc，根据排序不等式，得

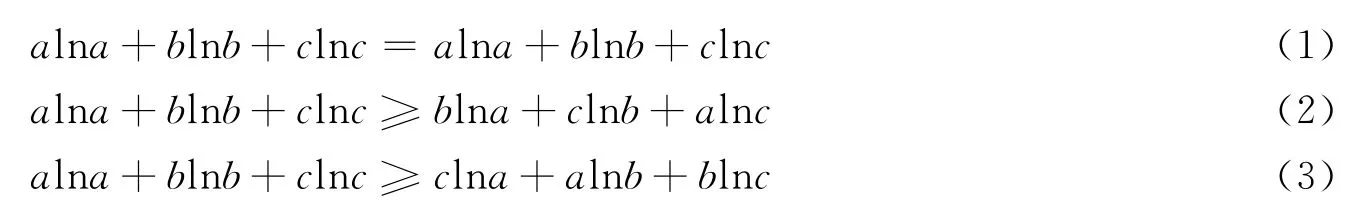
（1）＋（2）＋（3）得

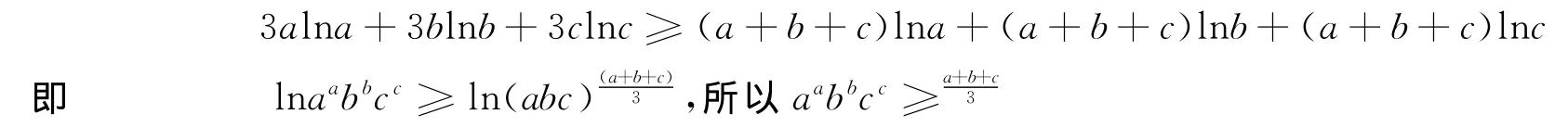
注 该证法关键是只有构造了两个有顺序的数组，才能利用排序不等式证明．

推广1：设ai∈ℝ＋（i＝1，2，…，n），求证

证明 序列｛ai｝与序列｛lnai｝有相同的大小顺序，根据（初等数学）切比雪夫不等式，

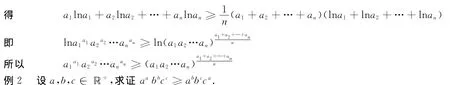
证明（用排序不等式）序列a，b，c，与序列lna，lnb，lnc，有相同的大小顺序，根据排序不等式，

得 alna＋blnb＋clnc≥blna＋clnb＋alnc

于是，有 lnaabbcc≥lnabbcca

即aabbcc≥abbcca

推广2 设ai∈＋（i＝1，2，…，n），an＋1＝a1，求证

推广3 设ai∈＋＋（i＝1，2，…，n），求证其中ji（i＝1，2，…，n）是1，2，3，…，n的任一排列．

上述推广2的不等式是推广3不等式的特殊情形．推广3的不等式的证明方法同例2．

证法1 原不等式等价于a2ab2bc2c≥ab＋cbc＋aca＋b，此不等式是新课标高中《不等式》［2］选讲中的习题．只需证

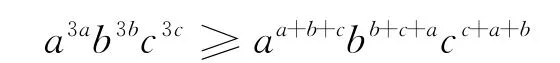
即等价于aabbcc≥（abc，而该不等式在例1中已证．故原不等式成立．

证法2 （商值比较法）由对称性，不妨设则a≥b≥c＞0，则

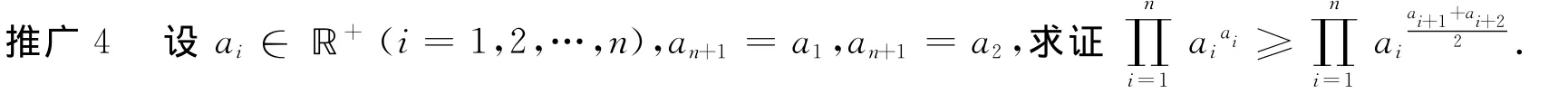
推广5 设ai∈ℝ＋（i＝1，2，…，n），求证，其中ki，mi（i＝1，2，…，n）分别是1，2，3，…，n的任一排列．

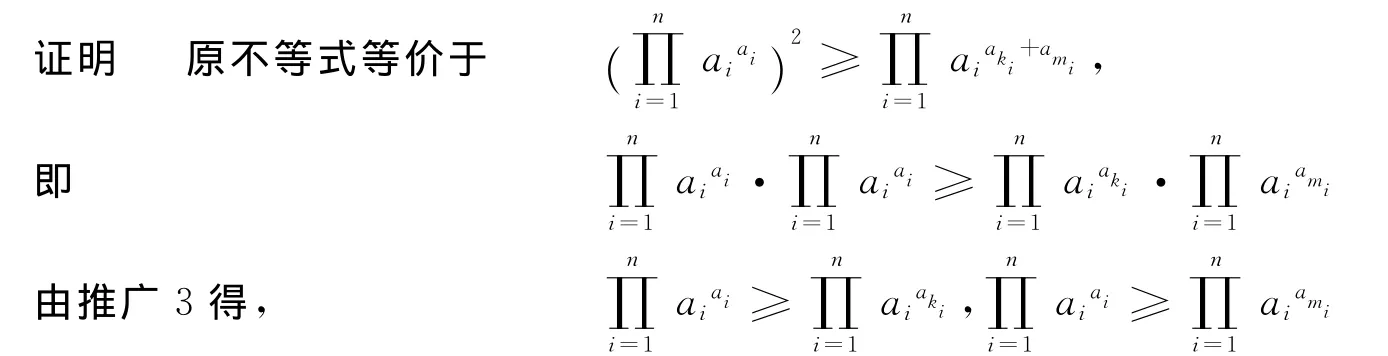
两不等式相乘，即证推广5．

上述推广4的不等式是推广5不等式的特殊情形．

由于例1、例2、例3中的三个不等式左边都相同，下面比较这三个不等式右边的幂的大小．例4 设a，b，c∈ℝ＋，记x＝（abc，y＝abbcca，z＝abc，则（1）x≥z；（2）不能确定y与z的大小；（3）不能确定x与y的大小。证明 1）x≥z

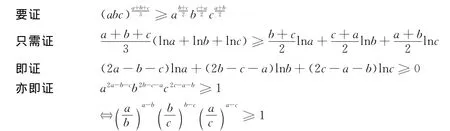
由对称性，不妨设则a≥b≥c＞0，则a－b≥0，b－c≥0，a－c≥0≥1，≥1，≥1．

故上不等式成立，即证．x≥z．

2）i）取a＝1，b＝2，c＝3时，y＞z；

iii）显然，可以使y＝z．

3）i）取a＝1，b＝1，0＜c＜1时，x＞y；

因此x＜y．

iii）显然，可以使x＝y．

由1）推广可得不等式：

推广6：设ai∈ℝ＋（i＝1，2，…，n，n≥3），求证

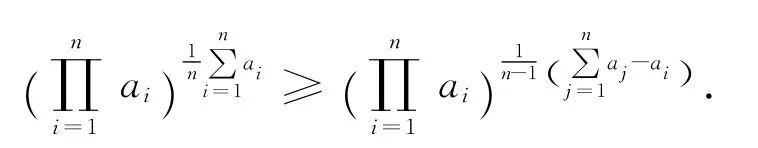
由不等式的对称性，不妨设a1≥a2≥…≥an，根据排序不等式，有

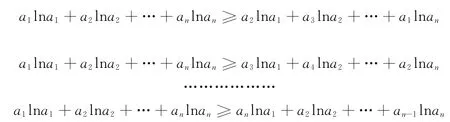
把上面n－1个不等式相加即证原不等式．

此不等式即为推广1．证毕．

［1］华东师范大学数学系．数学分析（上册）（第三版）．［M］．北京：高等教育出版社，2001．

［2］人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心．普通高中课程标准实验教科书，数学，不等式选讲［M］．北京：人民教育出版社，2007．

［3］余元希，田万海，毛宏德．初等代数研究下册［M］．北京：高等教育出版社，1988．

［4］余盛利，程 舰，文远航．詹森（Jensen）不等式在求几何最值与证明几何不等式中的应用［J］．湖北师范学院学报（自然科学版），2015，35（1）：105～109．

G250

A

009－2714（2016）04－0110－04

10．3969／j．issn．1009－2714．2016．04．024

2016—03—14

吴杉（1986— ），男，湖北荆门人，讲师，硕士，研究方向为微分方程与控制论．