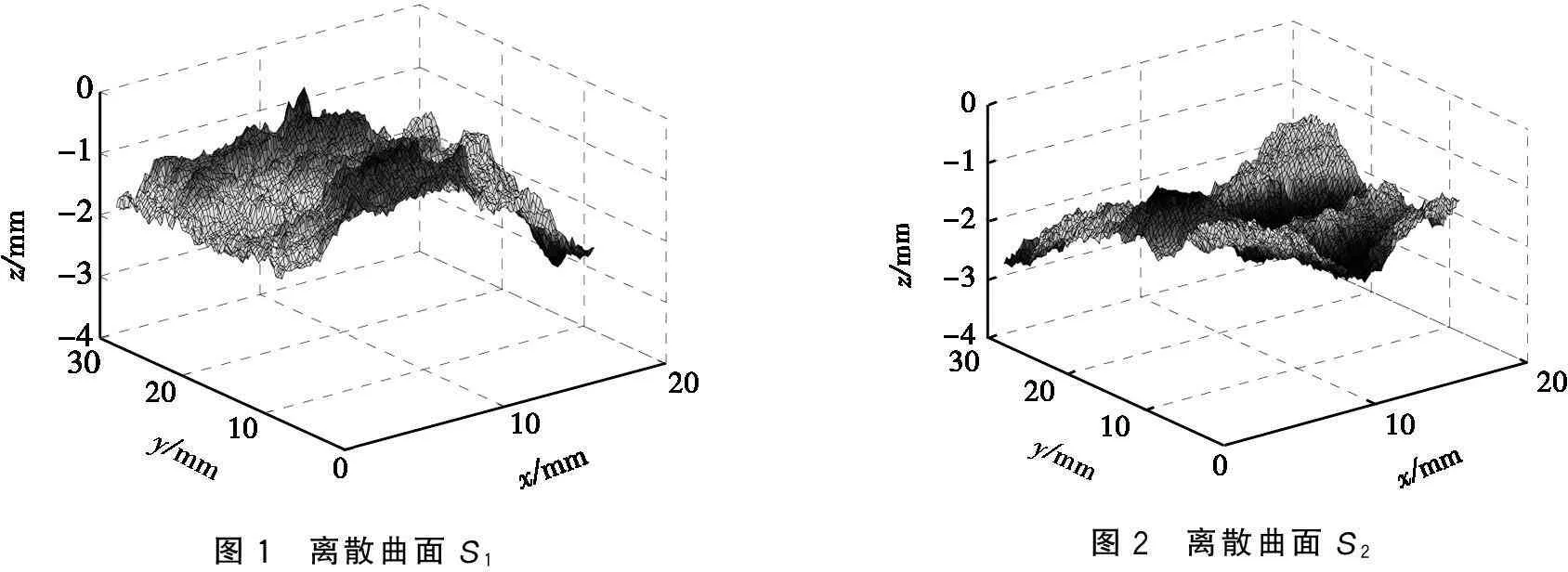
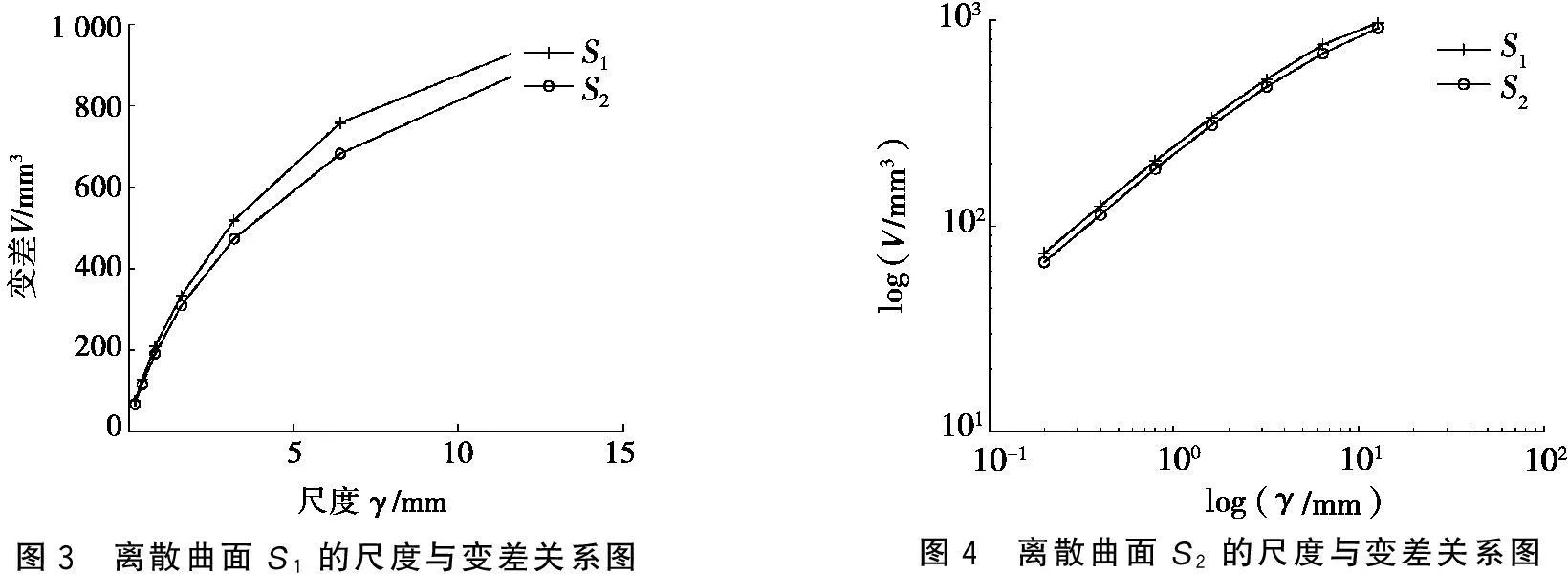
离散曲面变差的计算
2016-01-18郭艳芳冯志刚
郭艳芳,冯志刚
(江苏大学 理学院,江苏 镇江 212013)
离散曲面变差的计算
郭艳芳,冯志刚
(江苏大学 理学院,江苏 镇江 212013)
摘要:在连续函数变差相关理论基础上,为了更好地描绘实验或实际测得的曲面数据,本文引入离散曲面变差的概念,并提出了离散曲面变差的计算方法。针对两组不同的离散曲面数据,计算它们在不同尺度下的变差以及尺度和变差的双对数图,比较了两组离散曲面的维数与变差关系。研究结果表明:本文提出的离散曲面变差的计算方法是可行的,可以作为计算离散曲面变差的一种方法。
关键词:二元连续函数;离散曲面;振幅;变差
基金项目:国家自然科学基金项目(51079064)
作者简介:郭艳芳(1988-),女,山西吕梁人,硕士生;冯志刚(1962-),男,江苏常州人,教授,硕士生导师,主要从事分形几何理论的研究.
收稿日期:2014-07-04
文章编号:1672-6871(2015)02-0088-04
中图分类号:O244
文献标志码:志码:A
0引言
变差[1-4]作为刻画曲面粗糙度的一种重要参数,可以用来研究各种尺度下函数的粗糙度,而粗糙度在材料学、力学等学科中有着非常广泛的应用。研究自然界中各种材料、岩石、零件间的裂纹、断裂面的粗糙度,对研究裂纹的萌发、扩展以及最后导致材料断裂破坏这一整个过程的本质规律起着十分重要的作用。大量的研究已经证实断层、裂隙和节理的粗糙度,在采矿工程和土木工程中经常发生的滑坡及冒顶这些灾害性事故的发生中起着十分重要的作用。
文献[5]给出了连续函数的变差概念,对于连续函数f:I→,设δ>0,t∈I,称
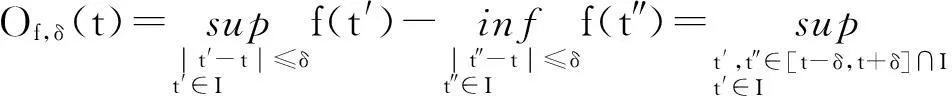
为f基于I在点t的δ-振幅,称Vf,δ(I)=∫IOf,δ(t)dt为函数f在I上的δ-变差。
文献[5]还研究了连续函数的δ-变差的性质,并给出二维平面上连续函数图像的计盒维数的计算公式,即设f:I→为连续函数,Γ(f,I)为f在I上的图像,则

文献[6]定义了三维空间中曲线的变差。而文献[7]在变差的基础上给出了三维空间中函数图像的计盒维数的公式。文献[8-9]介绍了二元连续函数的振幅和变差。对于在D上连续的函数y=f(x,y),设I=[a,b],J=[c,d]是的子集,D=I×J是2上的区域,δ、γ是非负实数;对任何(x,y)∈D,函数f(x,y)在点(x,y)∈D的(δ,γ)-振幅,记为(x,y),简记为Of;δ,γ(x,y)。且
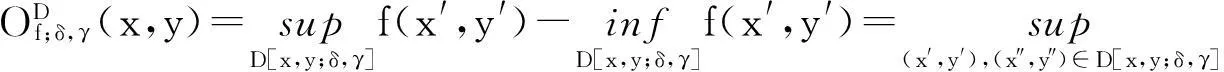
其中,D[x,y;δ,γ]=D∩([x-δ,x+δ]×[y-γ,y+γ])。函数f在区域D上的(δ,γ)-变差,记为Vf;δ,γ(x,y),且
Vf;δ,γ(x,y)=∬DOf;δ,γ(x,y)dxdy,
并证明了变差的一些性质,通过连续函数图像的计盒维数和它的变差之间的联系,得出了分形插值曲面的计盒维数公式[7-13]:

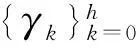
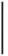
(1)
其中,G((xi,yj),γk)=([xi-γk,xi+γk]×[yj-γk,yj+γk])∩G。
离散曲面S:{(xi,yj,zij):i=1,2,…,m;j=1,2,…,n}的γk-变差为Vs(γk),且
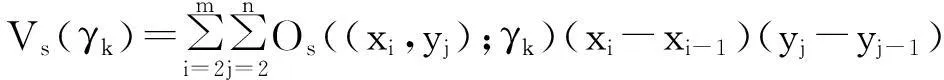
(2)
接着给出了离散曲面变差的计算方法,该方法在求尺度较大的离散曲面的变差时,有着明显的优势。例如:求离散曲面S中点(xi,yj)的γk-振幅,只需比较(xi-γk-1,yj-γk-1),(xi-γk-1,yj+γk-1),(xi+γk-1,yj-γk-1),(xi+γk-1,yj+γk-1)4点的最大值、最小值,不需要通过比较[xi-γk,xi+γk]×[yj-γk,yj+γk]中每一点的最大值、最小值求出每一点在尺度γk下的振幅,进而求出在尺度γk下的变差。
1离散曲面的变差计算
本文只讨论当曲面数据等距时,离散曲面的变差计算。
当曲面数据等距时,即xi-xi-1=yj-yj-1=ρ(常数),i=2,3,…,m;j=2,3,…,n。由曲面数据的离散特征,离散曲面的尺度γk可以取ρ的整数倍,特别地,可以取2进制的倍数γk=2kρ。其中,k∈Z,且0≤k≤log2max{m-1,n-1}。
下面研究γk=2kρ时离散曲面的变差算法,其中,0<γk≤max{xm-x0,yn-y0}。
由于式(1)也可表示为:
Os((xi,yj);γk)=max{zl,p:(xl,yp)∈G((xi,yj),γk)}-min{zl,p:(xl,yp)∈G((xi,yj),γk)},
所以对于i=0,1,2,…,m,m+1;j=0,1,2,…,n,n+1,计算
(3)
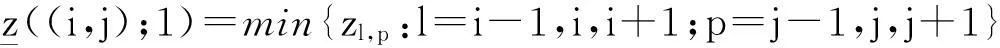
(4)
对于i=-2k+1,-2k+2,…,-2k+m;j=-2k+1,-2k+2,…,-2k+n,计算
(5)
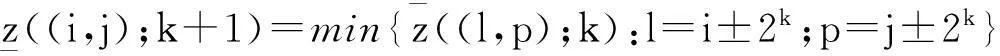
(6)
得到离散曲面S在(xi,yj)的γk-振幅为:
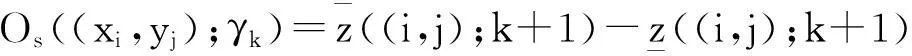
(7)
再计算曲面S的γk-变差:
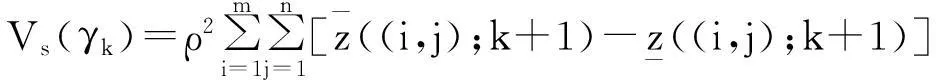
(8)
特别地,如果上述公式中的指标(l,p)超出前面计算出的范围,则不计在内。为了在计算机操作过程中解决这一问题,本文给出的算法程序中,针对已经给出的曲面数据扩充得到足够大的矩阵,从而解决了在式(3)~式(6)中指标(l,p)超出范围的问题。
由式(3)~式(8),本文设计了一个算法程序,其基本步骤如下:
步骤1把矩阵z=(zij)m×n扩充成一个新的矩阵B=(Bij)(2k+1+m)×(2k+1+n),
当1≤i≤2k+1且 1≤j≤2k+1时,B(i,j)=z(1,1);
2k+1 2k+n≤j≤2k+1+n时,B(i,j)=z(1,n)。 当2k+1 2k+1 2k+n≤j≤2k+1+n时,B(i,j)=z(i-2k,n)。 当2k+n≤j≤2k+1+n且1≤j≤2k+1时,B(i,j)=z(m,1); 2k+1 2k+n≤j≤2k+1+n时,B(i,j)=z(m,n)。 步骤2求矩阵B(i,j)在尺度γ=20·ρ下的最大值BM1(i,j),最小值Bm1(i,j),即 BM1(i,j)=max{B(i-1,j-1),B(i-1,j),B(i-1,j+1),B(i,j-1),B(i,j), B(i,j+1),B(i+1,j-1),B(i+1,j),B(i+1,j+1)}; Bm1(i,j)=min{B(i-1,j-1),B(i-1,j),B(i-1,j+1),B(i,j-1),B(i,j), B(i,j+1),B(i+1,j-1),B(i+1,j),B(i+1,j+1)}, 其中:2≤i≤2k+1+m-1;2≤j≤2k+1+n-1。 步骤3求矩阵B(i,j)在尺度γ=2t·ρ,1≤t≤k下的最大值BM1(i,j,t),最小值Bm1(i,j,t),其中,1+2t≤i≤2k+1+m-2t,1+2t≤j≤2k+1+n-2t,且 BM1(i,j,t)=max{BM1(i-2t,j-2t,t-1),BM1(i-2t,j+2t,t-1), BM1(i+2t,j-2t,t-1),BM1(i+2t,j+2t,t-1)}; Bm1(i,j,t)=min{Bm1(i-2t,j-2t,t-1),Bm1(i-2t,j+2t,t-1), Bm1(i+2t,j-2t,t-1),Bm1(i+2t,j+2t,t-1)}。 步骤4求B(i,j)在尺度γ=2k·ρ下的振幅Os(i,j)=BM1(i,j)-Bm1(i,j),其中2k+1≤i≤2k+1+m,2k+1≤j≤2k+1+n,则z(i,j)在尺度γ=2k·ρ下的变差为 Vs=ρ2·∑∑Os(i,j)。 2举例 给出离散曲面S1、S2,如图1和图2所示。 x1=0, x100=19.800, y1=8.212, y100=28.012, xi-xi-1=yj-yj-1=0.200, 其中:i=2,3,…100;j=2,3,…,100;xi、yj、zij的单位均为mm。 图1 离散曲面S1图2 离散曲面S2 计算得出两个离散曲面在不同尺度下的变差值,如表1所示。离散曲面S1、S2的尺度γ与变差V的关系图以及γ与V的双对数图,如图3和图4所示。 表1 离散曲面S1、S2在不同尺度下的变差值 图3 离散曲面S1的尺度与变差关系图图4 离散曲面S2的尺度与变差关系图 由图3可知:变差是反映曲面粗糙程度的重要参数。当尺度γ较小时,离散曲面S1、S2的变差很接近;随着尺度γ不断增大,离散曲面S1的变差较离散曲面S2的变差增幅大;且当尺度足够大以后,离散曲面S1的变差明显比离散曲面S2的变差大,离散曲面S1比离散曲面S2表现的粗糙,这与图1和图2是相符的。 图4表示log(Vs(γk)-log(λk))的双对数图像,与图3的变化规律是一致的。由曲面变差与计盒维数之间的关系,可以得出:离散曲面S1和S2的平均计盒维数分别为2.37和2.36,即离散曲面S1比离散曲面S2粗糙一些,这与已经得出的结果一致。 3结论 本文在连续函数变差的基础上,提出离散曲面变差的计算;并针对于等距的离散曲面数据,给出了离散曲面的变差计算方法;最后通过两个实例的结果验证了该方法的可行性以及正确性。 参考文献: [1]Tricot C.Curves and Fractal Dimension[M].New York:Spinger-Verlag New York Inc,1995. [2]Dubuc B,Tricot C.Variation d’une Function et Dimension de son Graph[J].Math Acad Sci Paris Ser:I,1988,306:531-533. [3]Tticot C.Funtion Norms and Fractal Dimension[J].SIAM J Math Anal,1997,28(1):189-212. [4]Dubuc B,Zucker S W,Tricot C,et al.Evaluating the Fractal Dimension of Surfaces[J].Proc R Soc Lond Ser:A,1989,425:113-127. [5]文志英.分形几何的数学基础[M].上海:上海科学技术出版社,2000. [6]冯志刚,王磊.分形差值函数的变差的性质[J].江苏大学学报:自然科学版,2005,26(1):49-52. [7]李玲,冯志刚,许荣飞.三维空间中函数图像的计盒维数[J].安徽工业大学学报,2007,24(1):113-116. [8]Feng Z G.Variation and Minkowski Dimension of Fractal Interpolation Surface[J].J Math Anal Appl,2008,345(1):322-334. [9]徐惠,冯志刚.一类分形插值函数的变差和计盒维数[J].安徽工业大学学报,2008,25(4):444-447. [10]黄艳丽,冯志刚.基于二次分形插值函数的分形插值曲面的变差与盒维数[J].河南科技大学学报:自然科学版,2011,32(3):68-71. [11]黄艳丽,冯志刚.基于分形插值函数的分形插值曲面的变差与计盒维数[J].工程数学学报,2012,29(3):393-398. [12]Feng Z G,Sun X Q.Box-counting Dimensions of Fractal Interpolation Surfaces Derived from Fractal Interploation Functions[J].J Math Anal Appl,2014,412(1):416-425. [13]毛北行,孟金涛.离散复杂网络系统的混沌同步[J].郑州大学学报:理学版,2013,45(3):9-12.