WANG Xiao-dong （王晓冬）， ZHU Guang-ya （朱光亚），2， WANG Lei （王磊）

1. School of Energy， China University of Geosciences （Beijing）， Beijing 100083， China，E-mail： wxd_cug@cugb.edu.cn

2. PetroChina Research Institute of Petroleum Exploration and Development， Beijing 100083， China

Exact analytical solutions for moving boundary problems of one-dimensional flow in semi-infinite porous media with consideration of threshold pressure gradient*

WANG Xiao-dong （王晓冬）1， ZHU Guang-ya （朱光亚）1，2， WANG Lei （王磊）1

1. School of Energy， China University of Geosciences （Beijing）， Beijing 100083， China，E-mail： wxd_cug@cugb.edu.cn

2. PetroChina Research Institute of Petroleum Exploration and Development， Beijing 100083， China

By defining new dimensionless variables， nonlinear mathematical models for one-dimensional flow with unknown moving boundaries in semi-infinite porous media are modified to be solved analytically. The exact analytical solutions for both constant-rate and constant-pressure inner boundary constraint problems are obtained by applying the Green's function. Two transcendental equations for moving boundary problems are obtained and solved using the Newton-Raphson iteration. The exact analytical solutions are then compared with the approximate solutions. The Pascal's approximate formula in reference is fairly accurate for the moving boundary development under the constant-rate condition. But another Pascal's approximate formula given in reference is not very robust for constant-pressure condition problems during the early production period， and could lead to false results at the maximum moving boundary distance. Our results also show that， in presence of larger TPG， more pressure drop is required to maintain a constant-rate production. Under the constant-pressure producing condition， the flow rate may decline dramatically due to a large TPG. What's more， there exists a maximum distance for a given TPG， beyond which the porous media is not disturbed.

threshold pressure gradient， moving outer boundary， analytical solution， porous media， transient pressure analysis， flow rate

Introduction

Moving boundary problems for porous flows have attracted much interest recently. In the petroleum reservoir engineering， the problem consists of inserting a Threshhold Pressure Gradient （TPG）. The TPG effect was experimentally observed， and it is shown that a certain nonzero pressure gradient is required for the initial flow［1，2］. Although the existing methods/solutions are sufficient for the lab applications， it might be advantageous to construct a simplified mathematical model to quantify the fluid flow performance. If we consider the unsteady flow of a typical non-Newtonian fluid-the Bingham's fluid in porous media，the moving boundary problem is posed due to the yield stress of the fluid［3-9］. A dimensionless governing equation of the Bingham non-Newtonian fluid flow is the same as that of the Newtonian fluid flow in presence of the threshhold pressure gradient. The mathematical model contains the governing equation and the boundary conditions. The model is non-linear and inhomogeneous because of the development of unknown moving boundaries. Finding an analytical solution for the nonlinear problem takes a tremendous effort.

Liu et al.［5］discussed analytical and numerical solutions for one-dimensional flow moving boundary problems in semi-infinite porous media with a TPG. However， their solutions obtained by the similarity transformation are very complicated， where the influence of the TPGs is not clearly shown. Pascal［3］also presented two approximate solutions by integral methods for moving boundary problems. Altrough the approximate solutions are clear and concise， but may not be accurate enough in some cases. In this paper，we propose two exact analytical solutions and our results show that the solutions of Liu et al.［5］are not robust. In addition， many scholars didn't consider the moving boundary effect［10-14］. Fractal characterization in the literatures is analyzed［15，16］.

The proposed exact analytical solutions can provide guidelines for oil recovery in low-permeability reservoirs.

1. Mathematical models

We propose a true analytical solution for mathematical models described by Yao et al.［6］. Considering a linear oil reservoir with low permeability shown in Fig.1， where the inner boundary is under either constant-rate or constant-pressure condition.

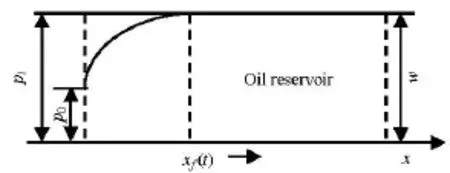
Fig.1 Illustration of the linear oil reservoir

A different definition for the dimensionless pressure and the TPG is employed to homogenize the outer boundary condition equation. Under the constant-rate inner boundary condition， the definitions are

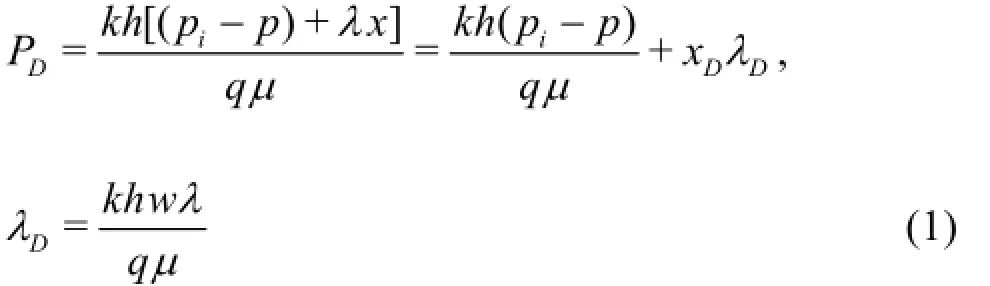
and under the constant-pressure inner boundary condition，

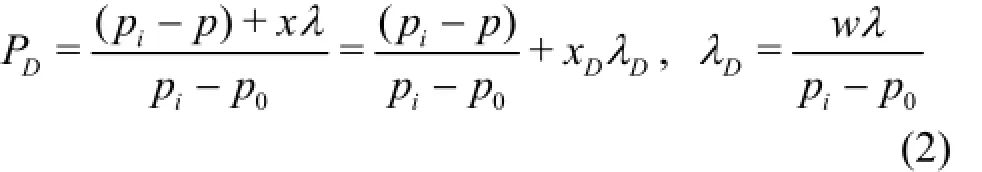
Other dimensionless variables are defined as follows：

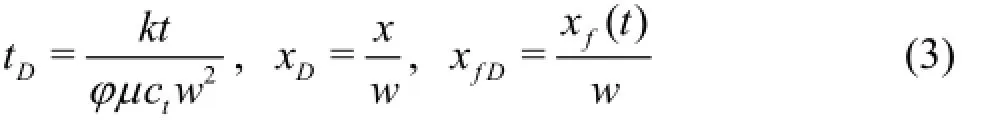
By the new definition of the dimensionless pressure and TPG， the equations［6］can be modified as

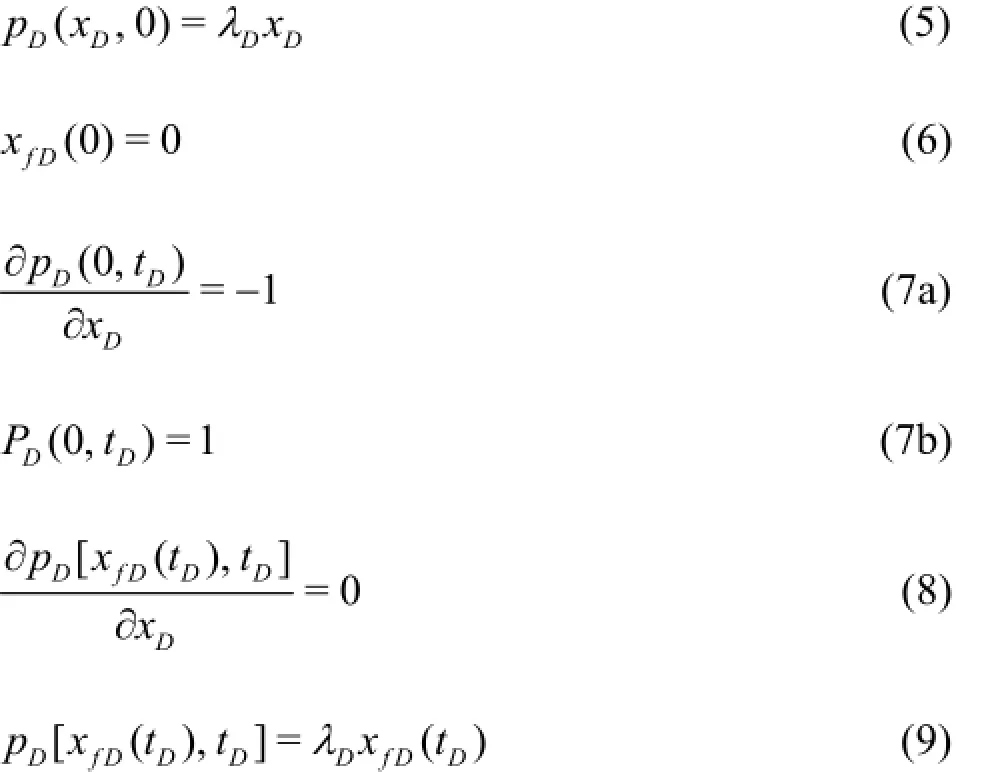
wherep is the pressure，piis the initial homogeneous pressure，p0is the constant pressure at the producing face，k is the formation permeability，his the reservoir thickness，qis the constant flow rate at the producing face，µis the Newtonian fluid viscosity andλis the TPG.

Equations （4）-（6）， （7a）， （8）， and （9） together form a dimensionless mathematical model for the one-dimensional flow with a TPG and a constant-rate inner boundary. To describe the constant-pressure inner boundary problems， just replace Eq.（7a） by Eq.（7b）.

2. True analytical solutions

Here two steps are taken to deduce the exact solution. First， we derive a pressure function in a fixed no-flow outer boundary （Eq.（8）） at a given dimensionless time. Second， we obtain the equation for the moving boundary development by combining the pressure function and the constant-pressure outer boundary（Eq.（9））.

2.1Analytical solution for the case of the constantrate inner condition

For the sake of the non-homogeneous initial condition， it is appropriate to apply the Green functions to derive the analytical solution［7］. A corresponding Green's function for the one-dimensional transient flow under Neumann's inner and outer conditions is as follows［8］

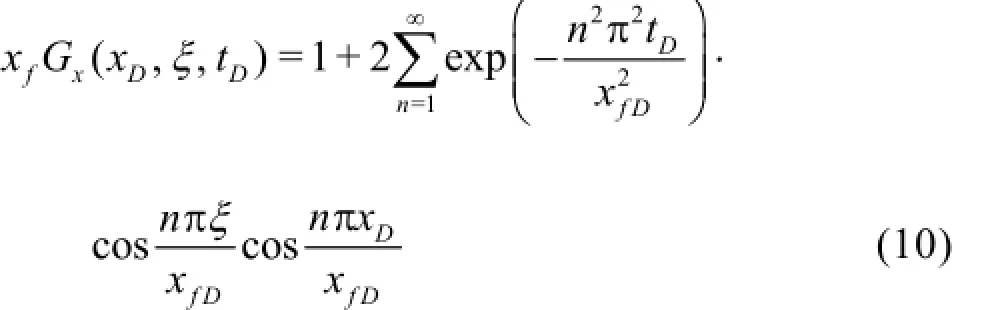
Then， the solution under the constant-rate inner condition and the fixed no-flow outer boundary is obtained as follows

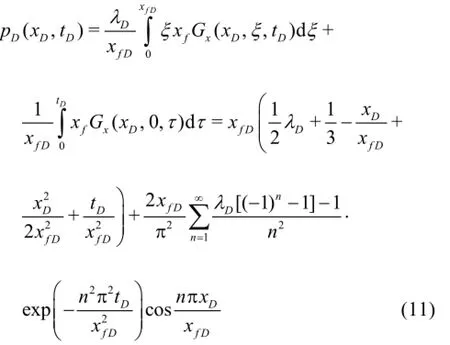
Substitutting Eq.（11） into Eq.（10）， we obtain

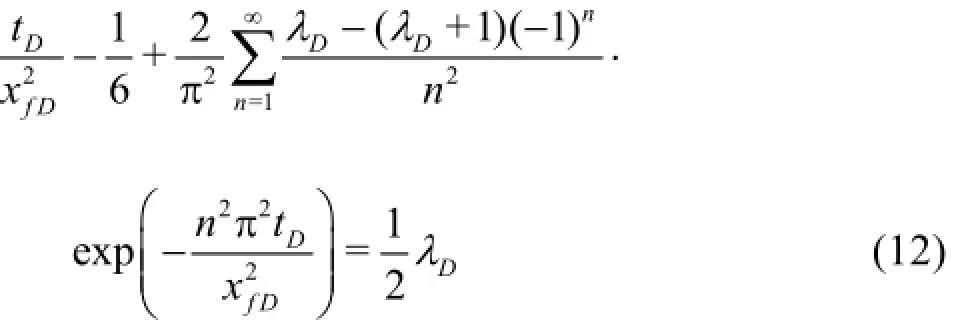
Roots of the transcendental equation （Eq.（12）） can be obtained by the method of Newton-Raphson iteration，and the dimensionless pressure distributions can be obtained using Eq.（11）.

Through the integral method， an approximate formula of the moving boundary development was presented by Pascal［3］as

and the dimensionless pressure function is

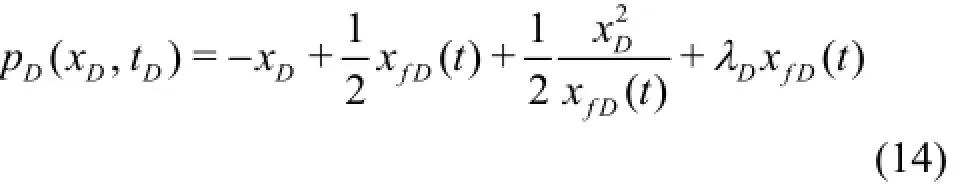
It is obvious to see that Eq.（13） is a special case of Eq.（12） where the summation item is ignored. These simple expressions will be used to verify our solutions.

2.2Analytical solution for constant-pressure inner condition problems

A Green's function for the one-dimensional transient flow under the Dirichlet's inner condition and the Newmann's outer boundary can be given as［8］：

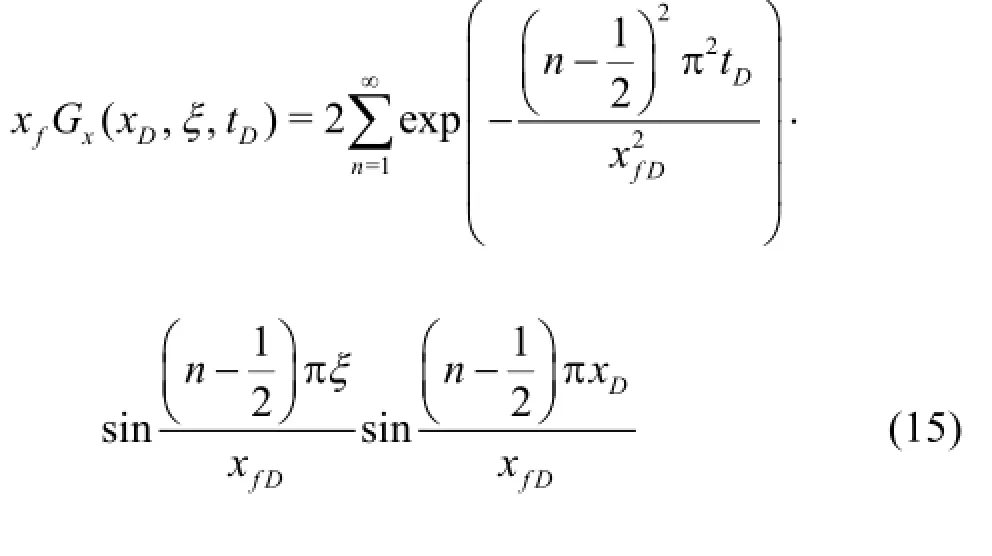
The solution under the constant-pressure inner boundary condition and under the fixed no-flow outer boundary condition can be obtained as follows

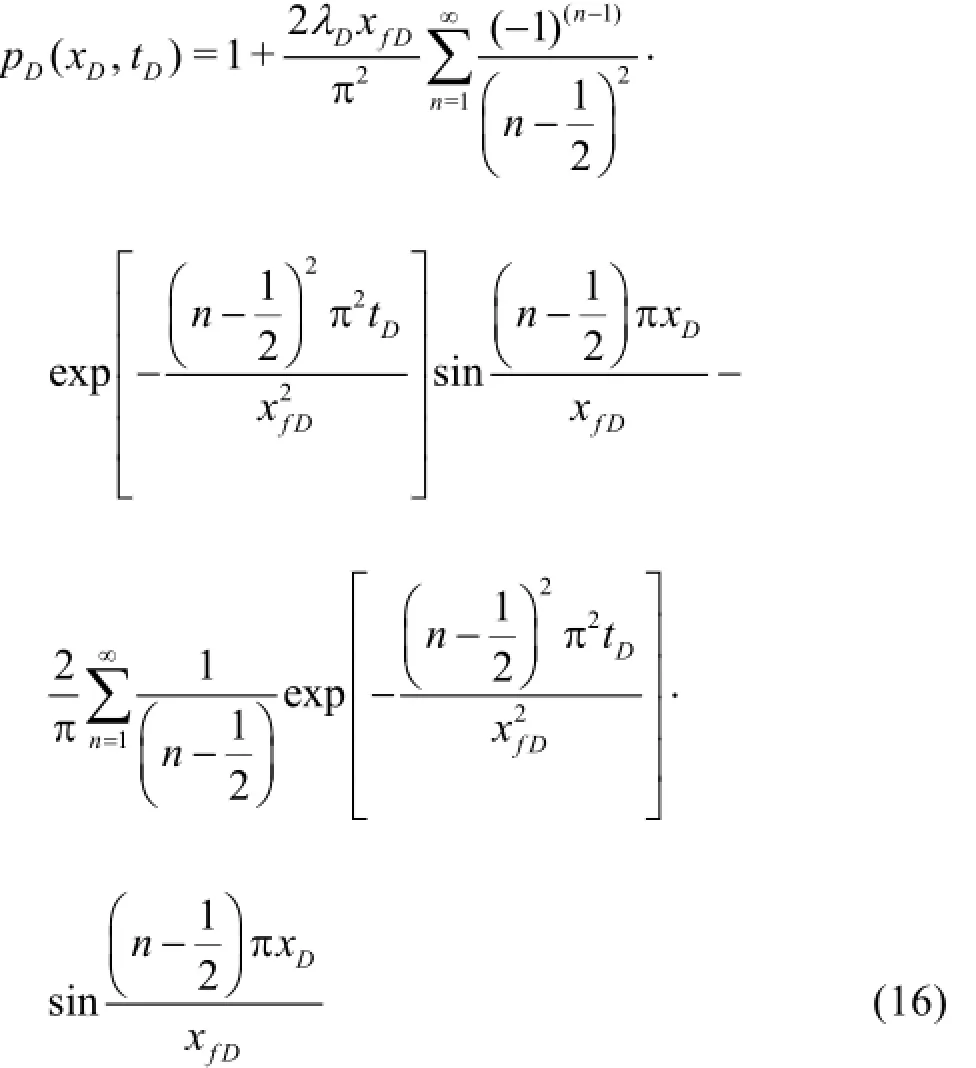
Substituting Eq.（16） into Eq.（15）， we obtain

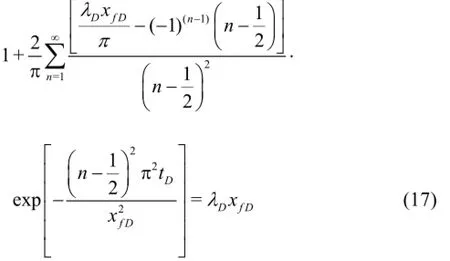
Similarly， a coarse approximate equation for this problem is given by Pascal［3］as

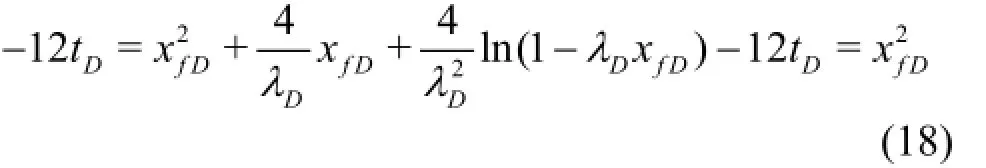
and the dimensionless pressure function is

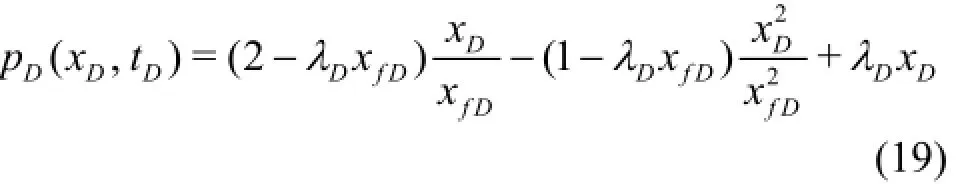
Eq.（18） may lead to false results when the moving boundary （xfD）approaches 1/λD.

We are interested in the flow rate at the producing face. The application of the Darcy's law to Eq.（16） gives

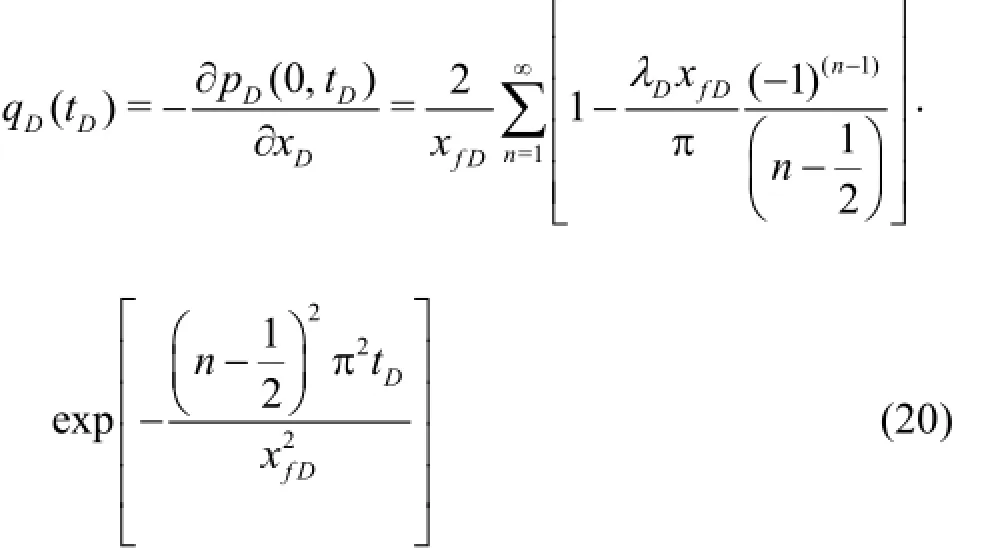
From Eq.（20）， it is clear that the flow rate is degressive with the time. As a special case of Eq.（20）， the solution obtained by Wattenbarger et al.［9］can be obtained if we set λD=0and xfDas a fixed outer boundary.

3. Results and Discussions

In Section 3， we have presented two transcendental equations for the moving boundary development. The transcendental equations can be solved by using the Newton-Raphson iteration［17，18］.

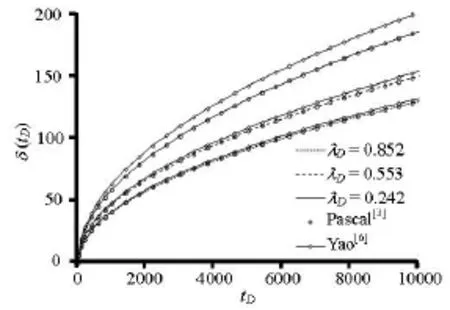
Fig.2 Comparison of moving boundary distance under the constant-rate inner condition

In this section， we compare our solution with the solutions given by Yao et al.［6］as well as Pascal［3］. Following Yao et al.［6］，λDare set to be equal to 0.242， 0.553， and 0.852. A base map is copied from the paper of Yao et al.［6］and the symbol δ（tD）in the base map is xfD（tD）in this study. Please note that all variables shown here are dimensionless.

Figure 2 shows the moving boundary distance against the dimensionless time for constant-rate inner boundary condition problems. From the plot， it is clear that， for a given λD， our result is consistent with Pascal's［3］solution， and Yao et al's solution gives a faster moving boundary. The smaller λDis， the larger the deviation between our solution and Yao et al's solution.

Fig.3 Comparison of moving boundary distance under the constant-pressure inner condition

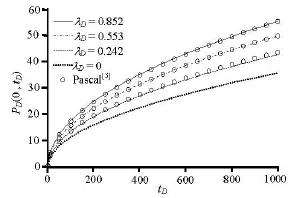
Fig.4 Comparison of dimensionless pressure at the constantrate producing face under different λD

Figure 3 shows the moving boundary distances against the time for constant-pressure inner boundary condition problems. We see that for a given λD， when tDis large enough，rfDbecomes a constant， which means there exists a maximum moving distance. Using Eq.（17）， it is easy to find out that the maximum distance is equal to 1/λDwhen tDapproaches 5（πλD2）. In such a case， the flow reaches a steadystate， and the pressure distribution is a straight line with a slope equal to λD. We can also see from the plot that， during early time period， Pascal's approximate expression （Eq.（18）） does not match our solution very well for smaller dimensionless TPGs.

Figure 4 shows the pressure against the time for constant-rate inner boundary problems for different TPGs. It is obvious that our solution matches well with Pascal's approximate solution. The larger the TPG， the more pressure drop is required to maintain a constant-rate production. While for a given TPG， it should be noted that the corresponding curve data of Yao et al.［6］is about large multiples of π under the same dimensionless pressure definition.

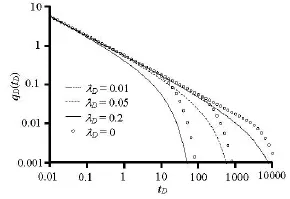
Fig.5 Comparison of dimensionless flow rate at the constantpressure producing face under different λD

Figure 5 shows the production against the time under a constant-pressure inner boundary condition for different TPGs. As already discussed， for a given λD， there is a maximum moving boundary distance under the constant-pressure inner boundary condition. The comparison shows that the flow rate declines more greatly under the impact of the TPGs than under a fixed outer boundary （that is the maximum moving boundary distance）. Some interesting reference curves using the maximum distance of the moving boundary as a fixed outer boundary other than TPGs， are completed to further illustrate the TPG effects.

4. Conclusions

（1） By redefining the new dimensionless variables in the Green's function， two analytical solutions are derived for one-dimensional flows with moving boundary in semi-infinite porous media.

（2） Our results show that under the constant-rate condition， the Pascal's approximate formula is robust. Under the constant-pressure condition， the Pascal's approximate formula deviates in some extent from the exact one during the earlier period which leads to some false results at the maximum moving boundary.

（3） It is shown that the larger the dimensionless TPG， the more pressure drop is required to maintain a constant-rate production.

（4） Under the constant-pressure production， the flow rate declines severely due to larger TPGs. It is also observed that there exists a maximum distance of the moving boundary for a given λD.

References

［1］HAO F.， CHENG L. S. and HASSAN O. et al， Threshold pressure gradient in ultra-low permeability reservoirs［J］. Petroleum Science and Technology， 2008， 26（9）：1035-1204.

［2］XIONG Wei， LEI Qun and GAO Shu-sheng et al. Pseudo threshold pressure gradient to flow for low permeability reservoirs［J］. Petroleum Exploration and Development， 2009， 36（2）： 232-236（in Chinese）.

［3］PASCAL H. Nonsteady flow through porous media in the presence of a threshold gradient［J］. Acta Mechanica， 1981， 39： 207-224.

［4］WU Y.， PRUESS K. and WITHERSPOON P. A. Flow and displacement of Bingham non-Newtonian fluids in porous media［J］. SPE Reservoir Engineering， 1992，7（3）： 369-376.

［5］LIU W.， YAO J. and WANG Y. Exact analytical solutions of moving boundary problems of one-dimensional flow in semi-infinite long porous media with threshold pressure gradient［J］. International Journal of Heat and Mass Transfer， 2012， 55（21-22）： 6017-6022.

［6］YAO J.， LIU W. and CHEN Z. Numerical solution of a moving boundary problem of one-dimensional flow in semi-infinite long porous media with threshold pressure gradient［J］. Mathematical Problems in Engineering，2013， Article ID 384246.

［7］LU J.， GHEDAN S.， Pressure behavior of vertical wells in low-permeability reservoirs with threshold pressure gradient［J］. Special Topics and Reviews in Porous Media， 2011， 2（3）： 157-169.

［8］CARSLAW H. S.， JAEGER J. C. Conduction of heat in solids［M］. Oxford， UK： Clarendon Press， 1984.

［9］WATTENBARGER R. A.， Ahmed H El-Banbi and MAURICIO E. V. Production analysis of linear flow into fractured tight gas wells［C］. 1998， SPE 39931.

［10］YAO Yue-dong， GE Jia-li. Characteristics of non-Darcy flow in low-permeability reservoirs［J］. Petroleum Science， 2011， 8（1）： 55-62.

［11］CIVAN F. Porous media transport phenomena［M］. Hoboken， NJ， USA： John Wiley and Sons， 2011.

［12］MONTEIRO P. J. M.， RYCROFT C. H. and BARENBLATT G. I. A mathematical model of fluid and gas flow in nanoporous media［J］. Proceedings of the National Academy of Sciences of the United States of America， 2012， 109（50）： 20309-20313.

［13］SONG Fu-quan， WANG Jian-dong and LIU Hai-li. Static threshold pressure gradient characteristics of liquid influenced by boundary wettability［J］. Chinese Physics Letters， 2010， 27（2）： 1-4

［14］ZENG B.， CHENG L. and LI C. Low velocity nonlinear flow in ultra-low permeability reservoir［J］. Journal of Petroleum Science and Engineering， 2012，80（1）： 1-6.

［15］CAI J.， YU B. and ZOU M. et al. Fractal analysis of invasion depth of extraneous fluids in porous media［J］. Chemical Engineering Science， 2010， 65（18）： 5178-5186.

［16］CAI J.， YU B. and ZOU M. et al. Fractal characterization of spontaneous co-current imbibition in porous media［J］. Energy and Fuels， 2010，24（3）： 1860-1867.

［17］NEDOMA J. Numerical solution of a Stefan-like problem in Bingham rheology［J］. Mathematics and Computers in Simulation， 2003， 61（3-6）： 271-281.

［18］XIE K. H.， WANG K. and WANG Y.-L. et al. Analytical solution for one-dimensional consolidation of clayey soils with a threshold gradient［J］. Computers and Geotechnics， ， 2010， 37（4）： 487-493.

（April 4， 2014， Revised July 28， 2014）

* Project supported by the Fundamental Research Funds for the Central Universities （Grant No. 2652014066）.

Biography： WANG Xiao-dong （1963-）， Male， Ph. D.，Professor