宫琴，任芳国

（陕西师范大学数学与信息科学学院，陕西西安710062）

关于弱受控不等式和矩阵范数不等式的研究

宫琴，任芳国

（陕西师范大学数学与信息科学学院，陕西西安710062）

受控理论和矩阵范数在矩阵理论中起着重要的作用，利用Weyl定理以及弱受控的一些结果，并通过置换矩阵的性质及矩阵绝对值的性质，获得了矩阵的一些受控不等式和矩阵范数的不等式。

弱受控；双随机矩阵；酉不变范数；矩阵范数

受控理论和矩阵范数在实际应用和计算中起了很大的作用，所以一直受到有关专家学者的关注。文献［1-2］通过弱受控的一些知识得到了矩阵奇异值构成的向量和特征值构成的向量的弱受控关系，文献［3］通过矩阵范数的性质得出有关矩阵范数的一些不等式，文献［4］给出了我们所需要的一些定义及引理，文献［5-8］详细介绍了矩阵的酉不变范数不等式，文献［9-10］得到一些分块矩阵的不等式，文献［11］介绍了双随机矩阵有关的不等式。本文利用置换矩阵的性质及矩阵绝对值得性质，获得了一些有关弱受控不等式和矩阵矩阵范数的不等式。

1　预备知识

为了叙述方便，对符号约定如下：Rn表示实数域上的n维列向量的集合，A*表示矩阵A的共轭转置矩阵，AT表示矩阵A的转置；Mm，n表示m×n阶矩阵的集合；tr（A）是矩阵A的迹，Mn表示n×n阶矩阵的集合。其他未加说明的符号参见文献［1］。

下面是与本文有关的几个定义及引理：

定义1［4］如果A=（aij）∈Mn的每行每列最多只有一个非零元素，这些非零元素只能是1，则称A是n阶的部分置换矩阵。

定义2［1］把置换矩阵中的元素1全部用绝对值是1的元素（实数或复数）替换后生成的矩阵，称为生成置换矩阵。

定义3［1］对任意A∈Mn，称矩阵为A的绝对值。

定义4［1］如果‖·‖是Mn上给定的酉不变范数，且‖·‖是矩阵范数当且仅当对于任意的A，B∈Mn，有‖AB‖≤‖A‖‖B‖。

引理1［1］设x=（xi），y=（yi）∈Rn，且xi≥0，yi≥0，那么x≺wy当且仅当存在一个次双随机矩阵Q∈Mn，使得x=Qy。

引理2［1］设A∈Mn是给定的非负矩阵，下面4条等价：

（Ⅰ）A为次双随机矩阵；

（Ⅱ）A可以扩张成一个双随机矩阵，也就是说A是一个双随机矩阵的左上角主子阵；

（Ⅲ）A是有限个部分置换矩阵的凸组合；

（Ⅳ）存在一个双随机矩阵S∈Mn，使得0≤A≤S。

引理3［4］设A∈Mn的奇异值按递减顺序排列

2　主要定理及证明

定理1（Ⅰ）Mn中的任意部分置换矩阵都能写成两个实的生成置换矩阵的凸组合；

（Ⅱ）设G∈Mn是生成置换矩阵，σ=（σ1，σ2，…，σn）T∈Rn，σi≥0，则diag（Gσ）的奇异值是σ1，σ2，…，σn；

（Ⅲ）设σ1≥σ2≥…≥σn≥0，s1≥s2≥…≥sn≥0，

（Ⅳ）设A1，A2，…，Am∈Mn有相同的奇异值σ1≥σ2≥…≥σn，令a（i）∈Cn是Ai主对角元素构成的向量，i=1，2，…，m。如果非负实数u1，u2，…，un满足u1+u2+…+un=1，那么弱受控于σ=（σ1，σ2，…，σn）T；

（Ⅴ）设A∈Mn，σ1≥σ2≥…≥σn≥0，A是有限个n×n矩阵的凸组合且这些矩阵的奇异值都是σ1， σ2，…，σn当且仅当，k=1，2，…，n。

证明：（Ⅰ）设A∈Mn为一个部分置换矩阵，A的第i行和第j列的元素全为0，A1∈Mn的第i行第j列的交叉元素是1，A2∈Mn第i行第j列的交叉元素是-1，A1，A2是实的生成置换矩阵，且A，A1，A2的其它各行各列元素1的位置一样，则有即对于任意的A∈Mn是部分置换矩阵，总能写成两个实的生成置换矩阵的凸组合。

（Ⅱ）设生成置换矩阵

则diag（Gσ）的奇异值为σ1，σ2，…，σn。

（Ⅲ）设s=｛si｝，σ=｛σi｝∈Rn，由k=1，2，…，n，可知s≺wσ。由引理1知，存在一个次双随机矩阵P∈Mn，使得s=Pσ。由引理2知，次双随机矩阵是有限个部分置换矩阵的凸组合，即，且为部分置换矩阵。

（Ⅳ）设Ai的奇异值分解Ai=VΣW*，V，W∈Mn是酉矩阵，且Σ=diag（σ1，σ2，…，σn），则

其中Pi是次双随机矩阵，i=1，2，…，n。

于是

而u1+u2+…+un=1，Pi为次双随机矩阵，那么u1P1+u2P2+…+unPn是次双随机矩阵，令

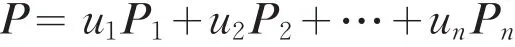
则P是次双随机矩阵，且

其中σ=（σ1，σ2，…，σn）T。

（Ⅴ）若A∈Mn是有限个矩阵的凸组合，且这些矩阵具有相同的奇异值，则设，其中有相同的奇异值σ1，σ2，…，σn，且σ1≥σ2≥…≥σn，A的奇异值分解A=VΣW*，V，W∈Mn是酉矩阵，Σ=diag（σ1（A），σ2（A），…σn（A）），且σ1（A）≥σ2（A）≥…≥σn（A）≥0，则有

设b（i）是V*AiW的主对角元素构成的列向量，由于Ai有相同的奇异值σ1，σ2，…σn，则V*AiW也有相同的奇异值σ1，σ2，…，σn，记σ=（σ1，σ2，…，σn）T，于是由（Ⅳ）结论知，存在次双随机矩阵Qi，使得

对于λ1+λ2+…+λn=1，

由引理1知，σ（A）≺wσ；反过来，若σ（A）≺wσ，再结合（Ⅲ）的结论有diag（σ1（A），σ2（A），…，σn（A））=，其中，Bi有相同的奇异值σ1，σ2，…，σn。

设A∈Mn的奇异值分解A=VΣW*，V，W∈Mn是酉矩阵，A的奇异值σ1（A）≥σ2（A）≥…≥σn（A）≥0，Σ=diag（σ1（A），σ2（A），…，σn（A）），则Σ=V*AW，于是，也就是

令Ai=VBiW*，则由奇异值的酉不变性知Ai有相同的奇异值σ1，σ2，…，σn，那么，其中Ai有相同的奇异值σ1，σ2，…，σn，且，也就是说A能写成有限个奇异值相同的矩阵的凸组合。

定理2设A，B是n阶方阵，A的奇异值分解A=VΣW*，其中V，W是酉矩阵，且

那么

（Ⅰ）|A|=WΣW*，且对于任意酉矩阵U∈Mn，有|UA|=|A|；

Λ=diag（λ1（H（A）），λ2（H（A）），…，λn（H（π））），λ1（H（A））≥λ2（H（A））≥…≥λn（H（A））；则对于任意给定的X∈Mn，总存在酉矩阵Z∈Mn，有Z|X| Z*≥H（A）；

（Ⅲ）总存在酉矩阵U1，U2∈Mn，使得。

证明：（Ⅰ）由A=VΣW*有

对于任意的酉矩阵U∈Mn。

（Ⅱ）由引理3，σk（A）≥λk（H（A）），k=1，2，…，n，于是

也就是Σ≥Λ，则对酉矩阵U∈Mn，有UΣU*≥UΛU*=H（A）。

由（Ⅰ）|A|=WΣW*≥0知Σ=W*|A|W≥0，（UW*）|A|（UW*）*=U（W*|A|W） U*=UΣU*≥H（A）令Z=UW*，则Z*Z=WU*UW*=I，故Z是酉矩阵。

因此，对任一给定的矩阵X∈Mn，存在酉矩阵V，W∈Mn，使得X=VΣW*，其中

Σ=diag（σ1（X），σ2（X），…，σn（X）），且H（A）有谱分解H（A）=UΛU*，其中U是酉矩阵，Λ=diag（λ1（H（X）），λ2（H（X）），…，λn（H（X））），总有Z|X| Z*≥H（X），其中Z=UW*是酉矩阵。

（Ⅲ）由于

由（Ⅱ）的结论知，存在酉矩阵U1，U2∈Mn，有

定理3设‖·‖是Mn上给定的酉不变范数，那么下面几条是等价的。（Ⅰ）‖·‖是Mn上的矩阵范数。（Ⅱ）对于任意的A∈Mn，总有‖Am‖≤‖A‖m，m=1，2，…。

（Ⅲ）对于任意的A∈Mn，总有‖A2‖≤‖A‖2。

（Ⅳ）‖E11‖≥1，其中E11∈Mn是只有第一行第一列的交叉元素是1，其余元素都是0的矩阵

（Ⅴ）对于任意的A∈Mn，总有‖A‖≥σ1（A），其中σ1（A）是A的最大奇异值。

证明：（Ⅰ）⇒（Ⅱ）。由A∈Mn是矩阵范数知，‖Am‖=‖Am-1A‖≤‖Am-1‖‖A‖≤…≤‖A‖m，A∈Mn

（Ⅱ）⇒（Ⅲ）。当m=2时，由（Ⅱ）知：‖A2‖≤‖A‖2。

（Ⅲ）⇒（Ⅳ）。因为‖E11‖2≥，而‖E11‖≠0，于是‖E11‖≥1。

（Ⅳ）⇒（Ⅴ）。设A∈Mn的奇异值分解A= U*ΣW，U，W∈Mn是酉矩阵，Σ是主对角元素是A的奇异值的对角矩阵，且

则由酉不变范数的性质有

于是有‖A‖≥σ1（A）。

（Ⅴ）⇒（Ⅰ）。对任意的k∈｛1，2，…，n｝，有Nk（AB）=（A）σi（B）≤Nk（σ1（A） B），于是由酉不变范数的等价定义可知

因此可知

故‖·‖是矩阵范数。

3　结论

在文献［1］和［3］的基础上，进一步研究了一些有关矩阵奇异值不等式，也涉及到一些受控不等式和有关矩阵范数的不等式。

［1］HORN R，JOHNSON A R.Matrix analysis［M］.Cambridge: Cambridge University Press，1985.

［2］HORN R A，Johnson C R.Topics in matrix analysis［M］. Cambridge:Cambridge University Press，1991.

［3］ZHAN X Z.Matrix inequalities［M］.Berln:Spinger-Verlag，2002.

［4］王桂松，吴密霞，贾忠贞.矩阵不等式［M］.北京:科学出版社，2006.

［5］ZHAN X Z.Inequalities involving Hadamard products and unitarily invariant norms［J］.Advances in Mathematics，1997，26（5）:477-478.

［6］ZHAN X Z.Inequalities for unitarily invariant norms［J］.Siam Journal on Matrix Analysis and Applications，1998，20（2）: 466-470.

［7］任林源，张利军.矩阵的酉不变范数不等式［J］.数学的实践与认识，2011，41（11）:204-208.

［8］黄介武.酉不变范数几何—算术平均值不等式的改进［J］.西南师范大学学报:自然科学版，2014，39（8）:1-4.

［9］ZHANG F Z.Schur complements and matrix inequalities in the lowner ordering［J］.Linear Algebra and Its Application，2000，321（1）:399-410.

［10］ZHANG F Z.Matrix inequalities by means of block matrices［J］.Mathematical Inequalities Applications，2001，4（4）: 481-490.

［11］ANDO T.Majorization，doubly stochastic matrices，and comparison of eigenvalues［J］.LinearAlgebra and ItsApplications，1989，118:163-248.

Research on InequalitiesAbout Weak Majorization and Matrix Norm

GONG Qin，REN Fangguo
（College of Mathematics and Information Science，Shaanxi Normal University，Xi'an 710062，Shaanxi，China）

Majorization theory and matrix norm play an important role in matrix theory。According to Weyl's theorem and some theorems about weak majorization，some results about inequalities of majorization and matrix norm are obtained by using Permutation matrix and absolute value of matrix。

weak majorization；substochastic matrices；unitarily invariant norms；matrix norm

O151.21

A

1672-2914（2015）06-0045-04

2015-07-06

国家自然科学基金项目（11471200）。

宫琴（1989-），女，山西忻州市人，陕西师范大学数学与信息科学学院硕士研究生，研究方向为矩阵论。

任芳国，副教授，E-mail:rfangguo@snnu.edu.cn。