朱自强，王灿，鲁光银，曹书锦



重力梯度张量解析信号的欧拉反褶积

朱自强，王灿，鲁光银，曹书锦

(中南大学 地球科学与信息物理学院，湖南 长沙，410083)

利用重力梯度张量数据高精度的特点以及解析信号在确定异常体位置上的优势，将重力梯度张量解析信号代替位场的导数完成重力梯度张量解析信号的欧拉反褶积；通过在1个窗口内对1组数据点解3个欧拉方程来自动识别构造指数，从而规避了传统欧拉反褶积方法中需要事先确定构造指数的问题，同时减少了背景场的影响。研究结果表明：使用重力梯度张量的解析信号，其欧拉反褶积的解收敛性很好，能准确地判断地下异常体源的位置，有效规避背景场的影响，反演效果较好。

重力梯度张量；解析信号；欧拉反褶积

重力梯度张量是重力位的二阶导数。传统的重力测量主要依靠密度的变化，重力梯度张量对微小的密度梯度的变化很敏感，因此，重力梯度张量能够更加灵敏地反映地下密度异常体，能够更加直接地反映场源体的边界范围[1]。解析信号是梯度值[2]，其振幅能够反映地下异常体的位置。将解析信号应用于重力场中，可以减少背景场的影响[3]，从而能够清晰地确定地下异常体的位置[4]。欧拉反褶积是一种能够自动或半自动地估算场源体的位置的反演方法，由于其在反演时所需使用的参数少，不需要知道场源密度或磁性等物性的先验信息，不需要精确的解释模型[5]，能快速而有效地反映地下异常源的边界。传统的欧拉反褶积需要事先确定或者列举出与场源性质有关的构造指 数，但当异常场中有多个源时，构造指数可能是变化的，而且在实际情况中，地下异常场源是未知的，因此，其构造指数难以确定，这样往往使得欧拉反褶积的解具有多解性和发散性。为了消除欧拉方程解的发散性问题，提取正确的欧拉解，FitzGerald[6]等采用了一种新的识别欧拉解方法，但是该方法不能评价欧拉解是否为优解。Mikhailov等[7]采用人工智能的方式提取欧拉方程的解。Gerovska等[8]在Stavrev等[9−10]提出的算法的基础上使用非聚类和聚类的方式处理欧拉解。Ugalde等[11]采用模糊聚类的方法来提取欧拉解，但该法过度地依赖人工来确定地下异常体源的个数。范美宁[12]提出水平梯度滤波法、基于主体异常距离准则的有效性统计筛选和构造指数的有效性筛选等改进措施[13−14]，将三维欧拉反褶积方法进行推广应用。曹书锦等[5]通过利用边缘检测张量不变量数据对异常体边界进行提取，来辅助剔除欧拉解中的发散解，取得了很好的效果。本文1个窗口内对1组数据点解3个欧拉方程[15]来最后通过模型算例进一步对比说明本文方法的有效性。

1 重力梯度张量及其解析信号

重力梯度张量即在笛卡尔坐标下重力位在，和方向的二阶导数，1个体积为、剩余密度为的质量体，其重力位表示为

其中：为观测点到场源之间的距离；为万有引力常量。重力梯度张量表示为

其二维振幅表示为

Nabighian[16]将二维解析信号推广到三维，Roset等[17]将位场的解析信号的定义进行扩展如下：

则其振幅可以表示为

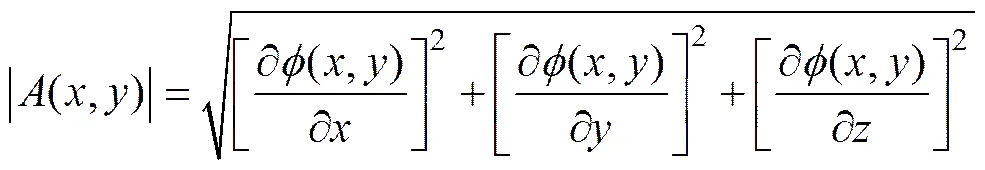
对于重力梯度全张量，其解析信号可用矩阵表示为

因此，振幅可以表示为

Debeglia等[18]提出解析信号振幅的一阶导数能更有效地分离目标异常体，对解析信号振幅求一阶导数表示为：

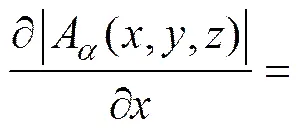
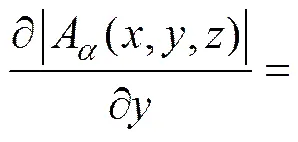
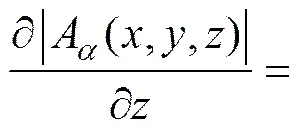
2 重力梯度张量欧拉反褶积

传统的欧拉反褶积是使用的正交梯度，表示为

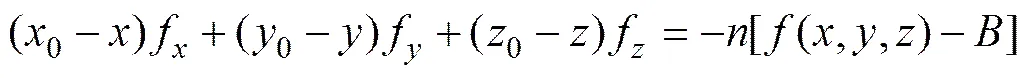
由于重力梯度张量是重力异常沿坐标系轴向的导数，因此，将传统欧拉方程推广到重力梯度张量的欧拉反褶积方程用矩阵表示为

其中：，和为背景场，由于背景场很小，故可忽略；，和为重力梯度；，，，，，，，和为重力梯度张量。

3 解析信号的欧拉反褶积

Keating等[19]使用欧拉反褶积有效地去除了解析信号的背景场。重力梯度张量解析信号的欧拉反褶积可以表述为

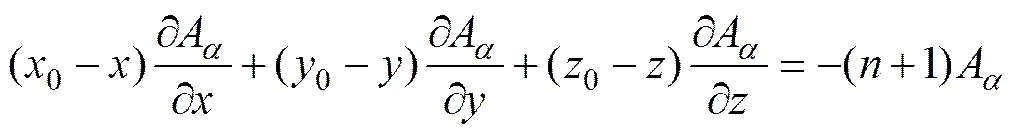
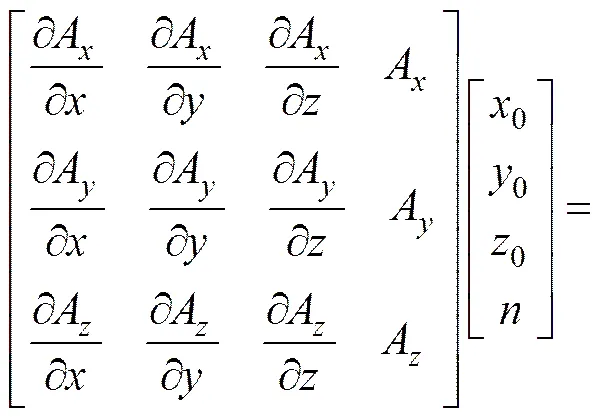
4 模型算例

以规则的球体和立方体作为研究模型，分别用重力梯度张量及其解析信号进行欧拉反褶积计算。

4.1 算例1：球体模型

球体模型设置：球体半径为1 km，球心坐标为 (0, 0, 1.5) km。剩余密度设为1 kg/m3，测网高度为0 m；在测区，设为−10~10 km，为−10~10 km；测网 长×宽为0.1 km×0.1 km。图1 所示为球体重力梯度张量解析信号的欧拉反褶积解，图1中黑点表示欧拉反褶积的解，黑色实线表示球体模型的轮廓线。图2所示为球体重力梯度张量的欧拉反褶积解。

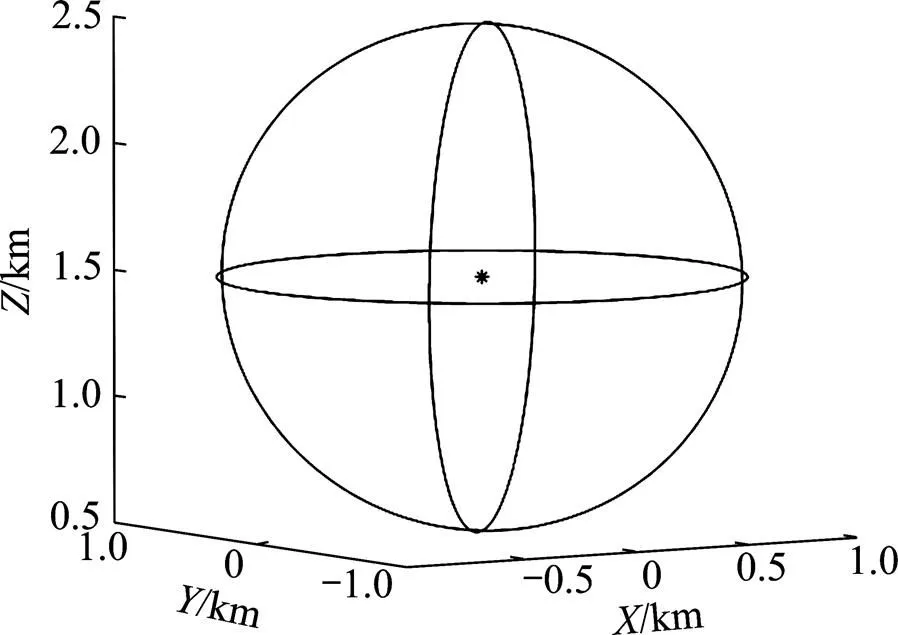
图1 球体重力梯度张量解析信号的欧拉反褶积解

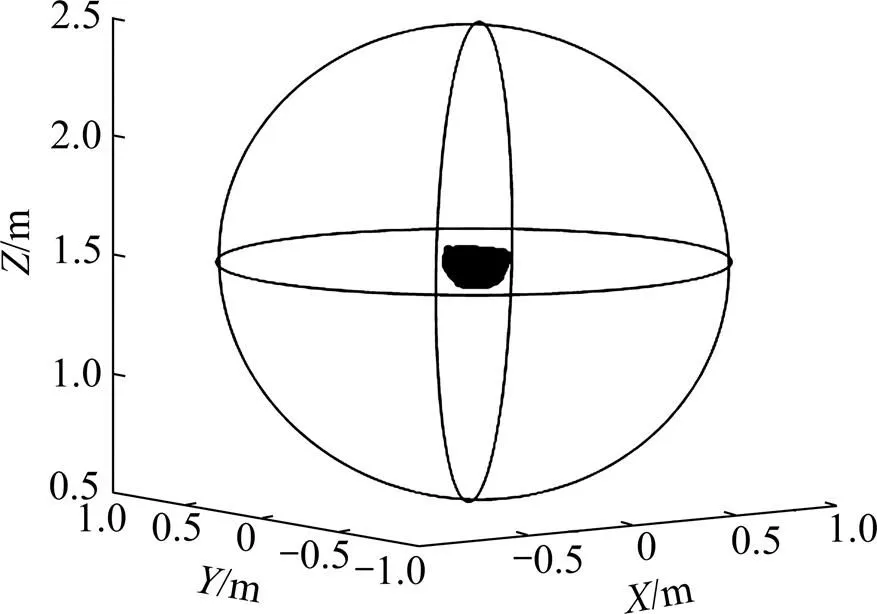
图2 球体重力梯度张量的欧拉反褶积解

对比图1和图2可见：对于同样的球体模型，使用重力梯度张量能较好地反映球体的球心位置，重力梯度张量的解析信号具有唯一解，能准确地描绘出球体场源的中心位置；欧拉解完全处于球体的中心部位。

从球体重力梯度张量解析信号欧拉反褶积结果可知：每个解在深度上都与模型设定值极吻合，构造指数与理论值完全相符，由此证明了本文方法的正确性。

4.2 算例2：立方体模型

立方体模型设置：立方体的长×宽×高为 0.6 km×0.6 km×0.6 km，质心坐标为(0, 0, 1.0) km。剩余密度设为1 kg/m3，测网高度为0 km。在测区，设为−10~10 km，为−10~100 km；测网长×宽为0.1 km×0.1 km。图3所示为立方体重力梯度张量解析信号的欧拉反褶积解，图4所示为立方体重力梯度张量解析信号的欧拉反褶积解，其中黑点表示欧拉反褶积的解，黑色实线表示立方体模型的轮廓线。

对比图3和图4可见：对于立方体模型，重力梯度张量的欧拉反褶积解大体汇聚在立方体的场源中心，欧拉反褶积解的底部较准确地反映了立方体的中心位置，但张量的欧拉反褶积解有一些向上延拓的发散解，对于圈定立方体场源中心可能带来不利的影响。从图3可以看出：使用重力梯度张量的解析信号之后，立方体的欧拉反褶积解很好地汇聚在立方体的场源中心，欧拉解完全处于立方体的中心部位。

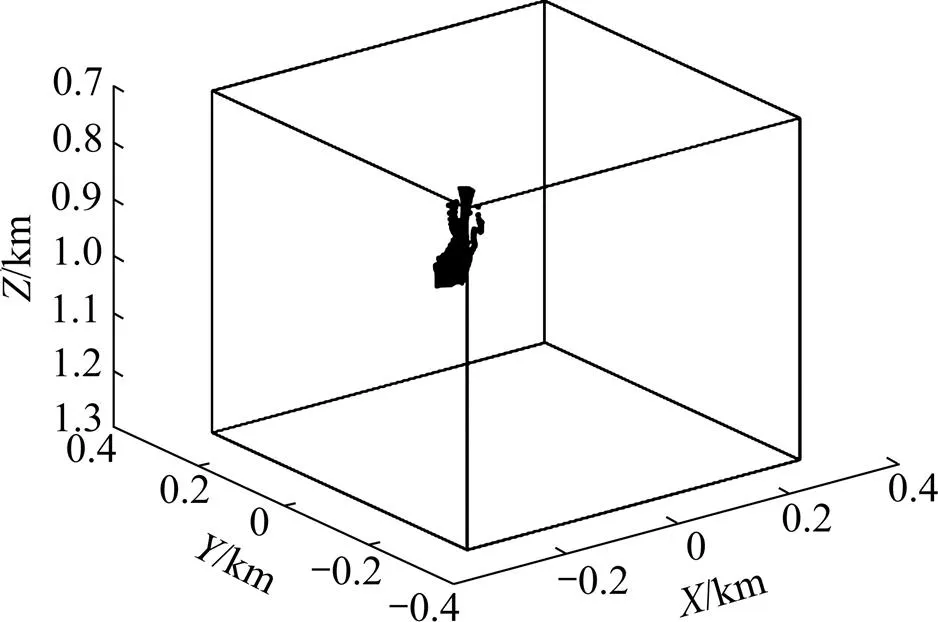
图3 立方体重力梯度张量的欧拉反褶积解

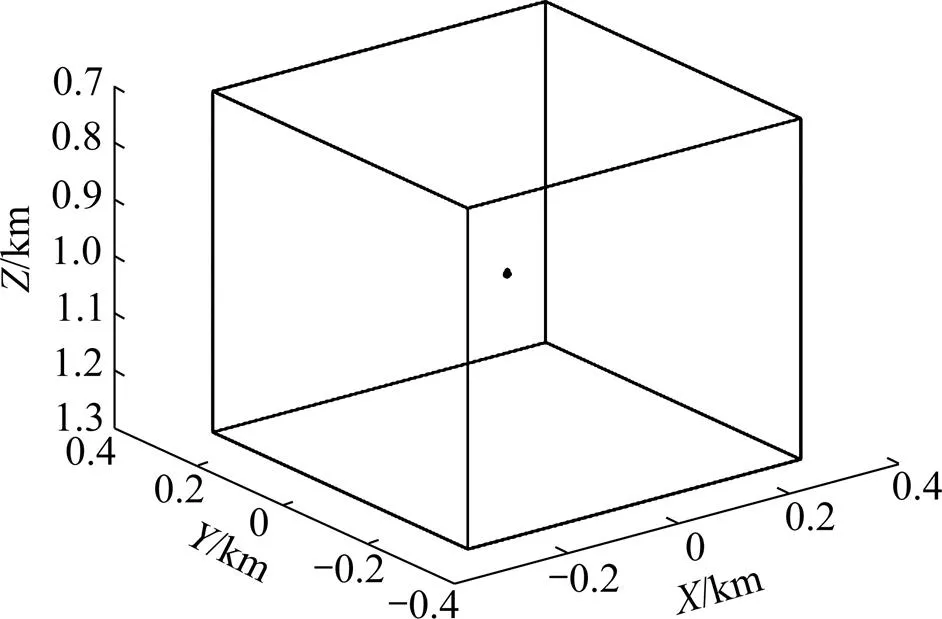
图4 立方体重力梯度张量解析信号的欧拉反褶积解

立方体张量解析信号进行欧拉反褶积的埋深和构造指数分别见图5和图6。从图5和图6可见：在前100个测点中，埋深大体在1.00 km的位置，上、下浮动在4.12 m之内，之后，变化很小；同样，前100个测点中，构造指数有极小的偏差，随后与理论值极吻合。这说明了该方法在确定单个模型位置和构造指数中的准确性。

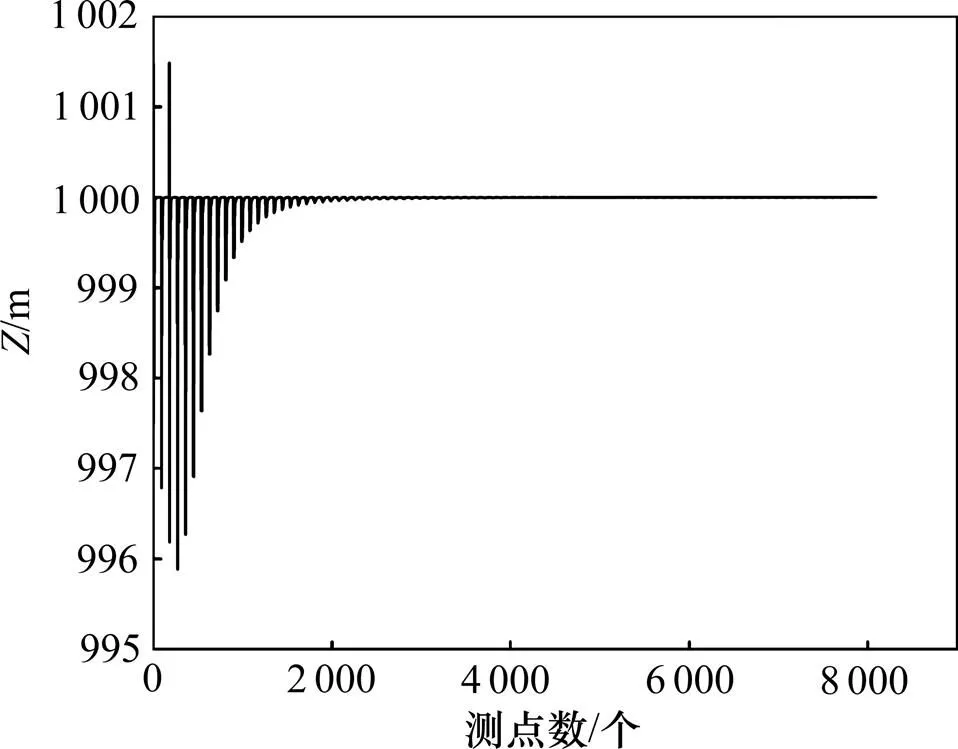
图5 立方体重力张量解析信号的欧拉反褶积埋深

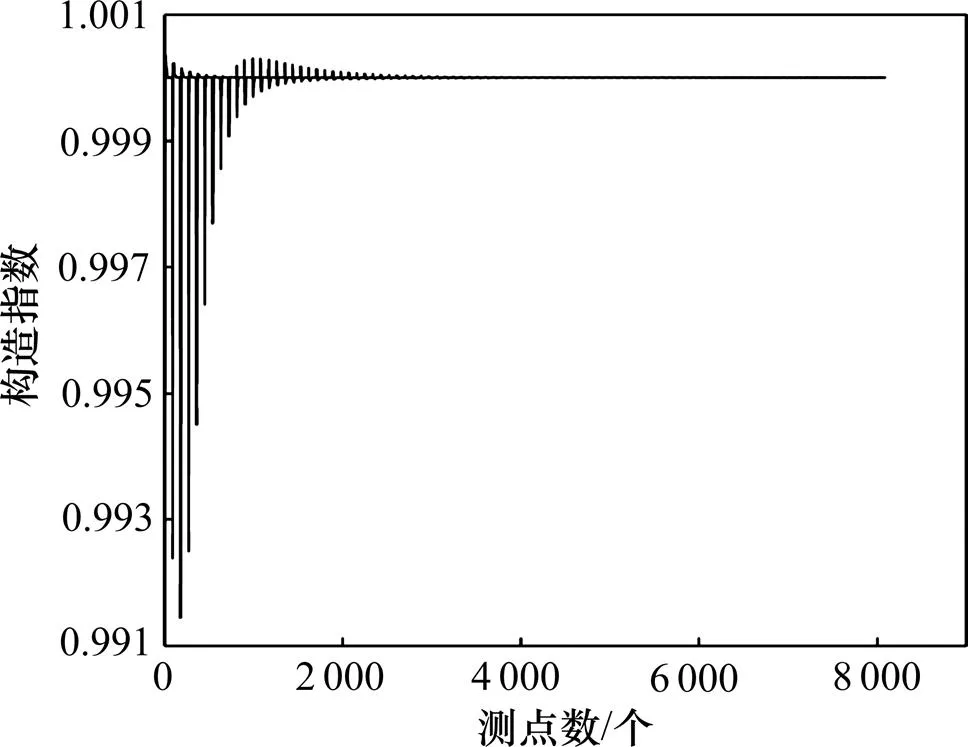
图6 立方体重力张量解析信号的欧拉反褶积构造指数

4.3 算例3：立方体叠加模型

将5个立方体叠加，立方体模型的质心坐标用 (0，0，0)表示，剩余密度设为1 kg/m3，测网高度为0 m。在测区，为−10~10 km，为−10~10 km；测网长×宽为0.1 km×0.1 km。模型几何参数设置如表1所示。

表1 模型几何参数

Table 1 Model geometrical parameters km

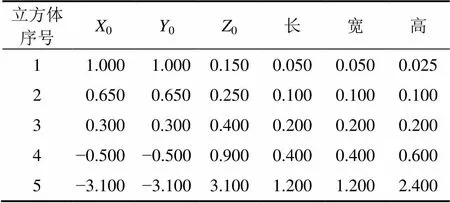
立方体序号X0Y0Z0长宽高 11.000 1.0000.1500.0500.0500.025 20.650 0.6500.2500.1000.1000.100 30.300 0.3000.4000.2000.2000.200 4−0.500−0.5000.9000.4000.4000.600 5−3.100−3.1003.1001.2001.2002.400

立方体叠加模型重力梯度张量分量的等值线图见图7。从图7可看出该叠加模型正演的正确性。

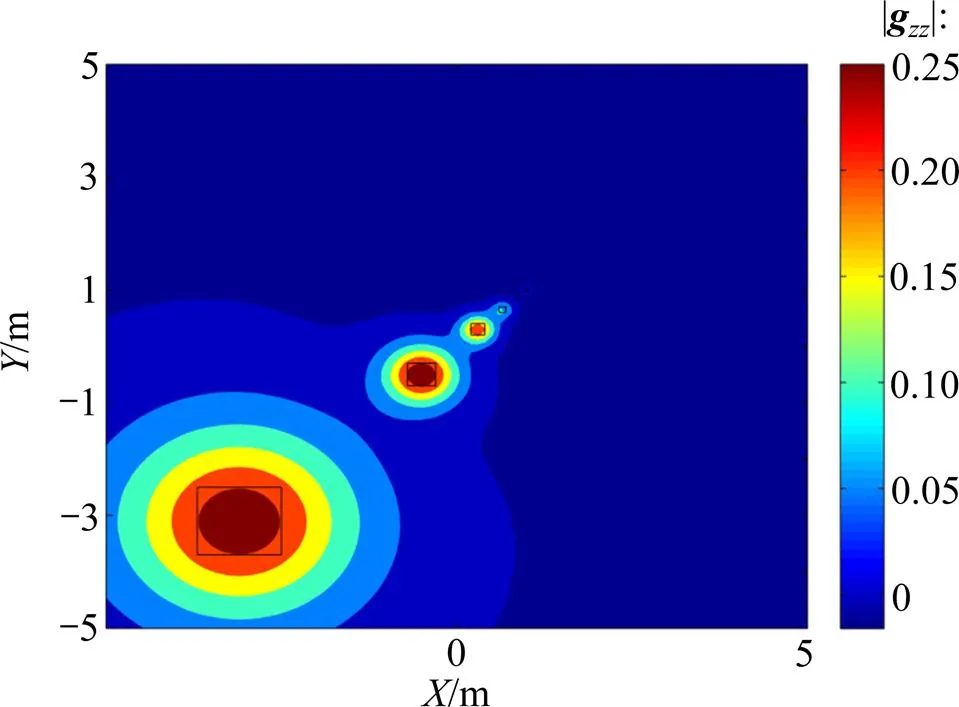
图7 立方体叠加模型重力梯度张量gzz分量的等值线图

对于规模较大的异常体(模型中的立方体5)，其解在总体欧拉解集中占有比较大的部分，相对较小规模尤其是靠近大规模异常体的小规模异常体(例如组合模型中的立方体3)，其异常源被淹没。图8和图9所示分别为立方体叠加模型的重力梯度张量解析信号欧拉反褶积解、重力梯度张量欧拉反褶积解。从图8可以看出，根据重力梯度张量的解析信号进行的欧拉反褶积解能准确、充分地判断出地下各个异常体源的位置情况。

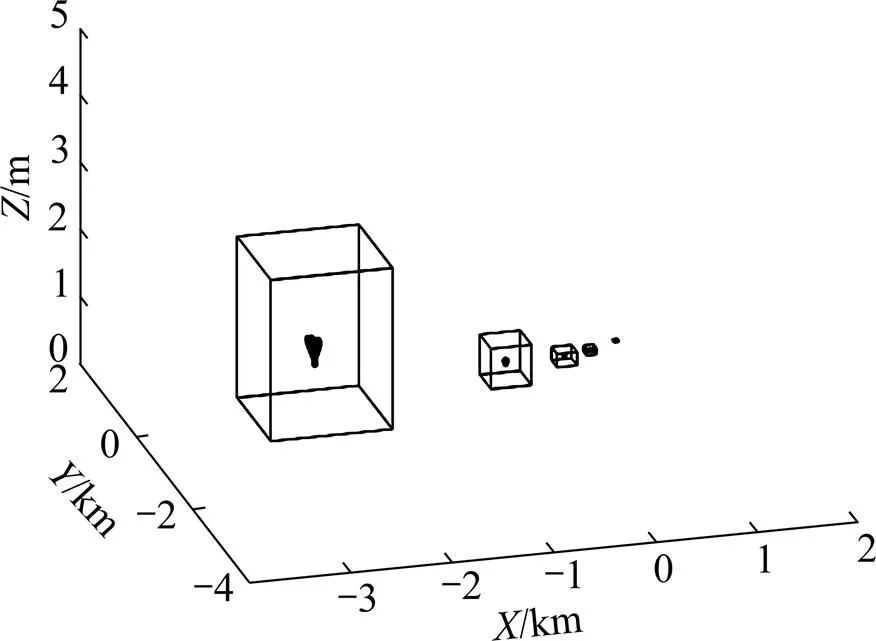
图8 立方体叠加模型重力张量解析信号的欧拉反褶积解

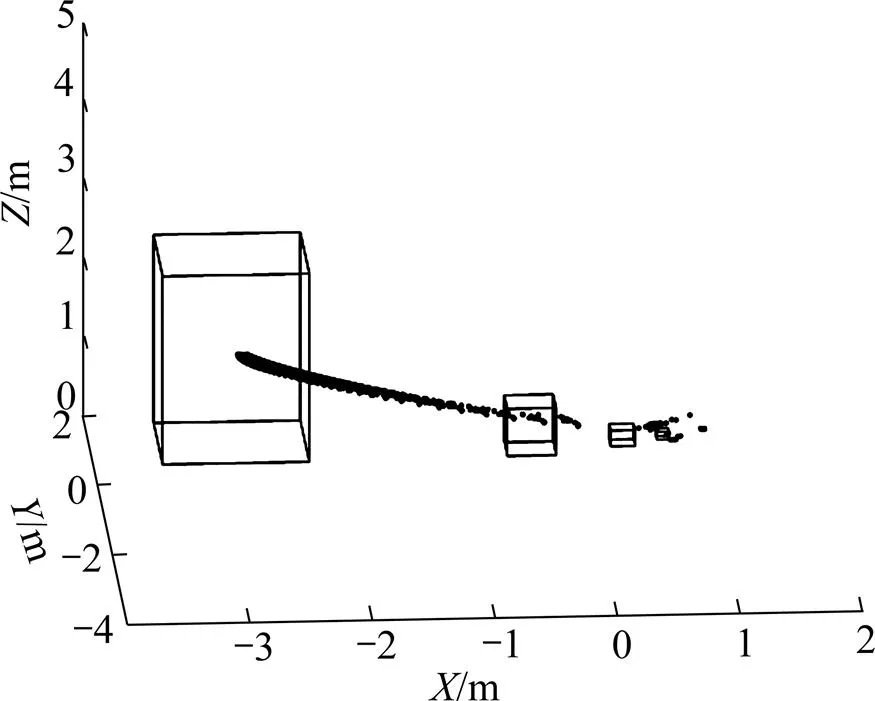
图9 立方体叠加模型重力张量欧拉反褶积解

据图9中仅可大致估计异常体的深度。

5 结论

1) 简单规则模型的重力梯度张量解析信号的欧拉解及其构造指数表明本文方法的正确性和可行性。

2) 重力梯度张量的解析信号能大大提高欧拉反褶积解的收敛性，改善了反演效果。这是由于本文算法中使用了重力位的三阶导数，而传统的重力张量欧拉反褶积只用到重力位的二阶导数。

3) 使用重力梯度张量解析信号能减少异常源间欧拉解的相互影响和干扰，因此，使用重力梯度张量的解析信号能有效规避背景场的影响。

4) 使用重力梯度张量的解析信号在1个窗口解3个欧拉方程，能在解的过程中自动识别构造指数，规避了传统欧拉反褶积方法中需要事先确定构造指数的问题，同时大大减少了背景场的影响。

5) 由于我国目前很难得到实测的梯度，解析信号数据需要经过计算得到，若能够获得直接的实测梯度和解析信号，或者使用某些技术手段来求取梯度和解析信号，压制其误差，则反演效果会得到更大改善。为了获得直接实测梯度数据和解析信号数据，需要加大对重力梯度仪的改进和推广使用。

[1] 曾思红. 重力梯度张量正演研究及边界提取[D]. 长沙: 中南大学地球科学与信息物理学院, 2010: 1−3.
ZENG Sihong. Gravity gradient tensor forward research and edge extraction[D]. Changsha: Central South University. School of Geosciences and Info-Physics, 2010: 1−3.

[2] 王万银. 位场解析信号振幅极值位置空间变化规律研究[J]. 地球物理学报, 2012, 55(4): 1288−1299.
WANG Wanyin. Spatial variation law of the extreme value position of analytical signal amplitude for potential field data[J]. Chinese J Geophys, 2012, 55(4): 1288−1299.

[3] 张季生, 高锐, 李秋生, 等. 欧拉反褶积与解析信号相结合的位场反演方法[J]. 地球物理学报, 2011, 54(6): 1634−1641.
ZHANG Jisong, GAO Rui, LI Qiusen, et al. A combined Euler and analytic signal method for an inversion calculation of potential data[J]. Chinese J Geophys, 2011, 54(6): 1634−1641.

[4] Beiki M. Analytic signals of gravity gradient tensor and their application to estimate source location[J]. Geophysics, 2010, 75(6): 59−74.

[5] 曹书锦, 朱自强, 鲁光银. 基于自适应模糊聚类分析的重力张量欧拉反褶积解[J]. 中南大学学报(自然科学版), 2012, 43(3): 1033−1039.
CAO Shujin, ZHU Ziqiang, LU Guangyin. Gravity tensor Euler deconvolution solutions based adaptive fuzzy cluster analysis[J]. Journal of Central South University (Science and Technology), 2012, 43(3): 1033−1039.

[6] FitzGerald D, Reid A, McInerney P. New discrimination techniques for Euler deconvolution[J]. Computers and Geosciences, 2004, 30(5): 461−469.

[7] Mikhailov V, Galdeano A, Diament M, et al. Application of artificial intelligence for Euler solutions clustering[J]. Geophysics, 2003, 64(2): 168−180.

[8] Gerovska D, Araúzo-Bravo M J. Automatic interpretation of magnetic data based on Euler deconvolution with unprescribed structural index[J]. Computers & Geosciences, 2003, 29(8): 949−960.

[9] Stavrev P Y. Euler deconvolution using differential similarity transformations of gravity or magnetic anomalies[J]. Geophysical Prospecting, 1997, 45(2): 207−246.

[10] Stavrev P Y, Gerovska D, Arauzo-Bravo M J. Depth and shape estimates from simultaneous inversion of magnetic fields and their gradient components using differential similarity transforms[J]. Geophysical Prospecting, 2009, 57(4): 707−717.

[11] Ugalde H, Morris W A. Cluster analysis of euler deconvolution solutions: new filtering techniques and geologic strike determination[J]. Geophysics, 2010, 75(3): L61−L70.

[12] 范美宁. 欧拉反褶积方法的研究及应用[D]. 长春: 吉林大学地球探测科学与技术学院, 2006: 62−63.
FAN Meining. The study and application of Euler deconvolution method[D]. Changchun: Jilin University. Geo-Exploration Science and Technology Institute, 2006: 62−63.

[13] 姚长利, 管志宁, 吴其斌, 等. 欧拉反演方法分析及实用技术改进[J]. 物探与化探, 2004, 28(2): 150−155.
YAO Changli, GUAN Zhining, WU Qibin, et al. An analysis of Euler deconvolution and its improvement[J]. Geophysical & Geochemical Exploration, 2004, 28(2): 150−155.

[14] 王家林. 对我国石油重磁勘探发展的几点思考[J]. 勘探地球物理进展, 2006, 29(2): 82−86.
WANG Jialin. Views on the domestic situation and progress of gravity and magnetic petroleum exploration[J]. Progress in Exploration Geophysics, 2006, 29(2): 82−86.

[15] 范美宁, 江裕标, 张景仙. 不同数据用于欧拉方程的模型计算[J]. 地球物理学进展, 2008, 23(4): 1250−1253.
FAN Meining, JIANG Yubiao, ZHANG Jingxian. Model calculation of Euler’s equation for different data types[J]. Progress in Geophysics, 2008, 23(4): 1250−1253.

[16] Nabighian M N. Toward a three-dimensional automatic interpretation of potential field data via generalized Hilbert transforms: Fundamental relations[J]. Geophysics, 1984, 49(5): 780−786.

[17] Roest W R, Verhoef J, Pilkington M. Magnetic interpretation using the 3-D analytic signal[J]. Geophysics, 1992, 57(1): 116−125.

[18] Debeglia N, Corpel J. Automatic 3-D interpretation of potential field data using analytic signal derivatives[J]. Geophysics, 1997, 62(1): 87−96.

[19] Keating P, Pilkington M. Euler deconvolution of the analytic signal and its application to magnetic interpretation[J]. Geophysical Prospecting, 2004, 52(3): 165−182.

Euler deconvolution of analytic signals of gravity gradient tensor

ZHU Ziqiang, WANG Can, LU Guangyin, CAO Shujin

(School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

Depending on high resolution of gravity gradient tensor data as well as the advantage of determining the location of gravity anomalies by the analytic signal, Euler deconvolution of the analytic signal of gravity gradient tensor was solved by analytic signal instead of gravity field derivatives. Structural index was automatically identified by a set of data points in a window solving Euler equations, so there was no need to determine structural index in advance and denoise background field which traditional Euler deconvolution method had. The results show that Euler deconvolution solution converges quickly, the disturbance of background field can be eliminated effectively, and the results of this method are useful and robust.

gravity gradient tensor; analytic signal; Euler deconvolution

P631.1

A

1672−7207(2015)01−0217−06

2014−01−10；

2014−03−12

国家自然科学基金项目资助(41174061) (Project(41174061) supported by the National Natural Science Foundation of China)

鲁光银，博士，教授，从事地震及重磁相关领域的研究；E-mail: csulgy@163.com

10.11817/j.issn.1672−7207.2015.01.029

(编辑 陈灿华)