ZHANG Dao-xiang, CHENG Hang

(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000， China)

Exact Solutions for Unsteady Riabouchinsky Flow of Couple Stress Fluids

ZHANG Dao-xiang, CHENG Hang

(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000， China)

This paper aims to investigate analytical solutions for the Riabouchinsky time-dependent flows of couple stress fluids. By assuming certain forms of the streamfunction, we obtain some exact steady and unsteady solutions. The results show that streamfunction and velocity components are all strongly dependent upon the material parameter of couple stress fluids.

couple stress fluid; newtonian flow; Riabouchinsky flow

Classification No: O175 Document code:A Paper No:1001-2443(2015)05-0414-05

Couple stress fluids, such as blood fluids, lubricants and electro-rheological fluids, are particularly important because of their widespread industrial and scientific applications[1-5]. The main characteristic of couple stress fluids is that the stress tensor is anti-symmetric and their accurate flow behaviour can’t be predicted by the classical Newtonian theory. To obtain exact solutions, a common method is to assume certain physical or geometrical properties of the flow field aprior and solve the equations by this method described by Nemenyi[6]. The flow problems of Newtonian fluid, second-grade fluid and couple stress fluid have been also studied by this method[7-9].

Taking the streamfunction to be linear in one of the space dimensions, Riabouchinsky[10]investigated the steady caseψ(x,y)=yf(x).Hayatet.al[11-12]gaveanalternateapproachtofindexactsolutionsofRiabouchinskyflowsofasecondgradefluidforsteadyandunsteadycases.Inthispaper,theanalyticalsolutionsforunsteadyRiabouchinskyflowsofcouplestressfluidsareconstructed.Meanwhilethestreamlinesareplottedinsomecasestounderstandtheflowbehavior.

1 Basic Equations

The flow of a viscous incompressible non-Newtonian couple stress fluid, neglecting thermal effects and body forces, is governed by (Stokes[1]):

(1)

(2)

Letusconsidertheplanemotionofanunsteadycouplestressflowinwhichthevelocityfieldisoftheform

(3)

and the generalized pressurep′andvorticityωfunctionsaredefinedas

(4)

(5)

Substitution of (3), (4) and (5) in equations (1) and (2), and elimination of the generalized pressure by cross differentiation yields

(6)

(7)

Continuity equation (6) implies the existence of a streamfunctionψ(x,y,t)suchthat

(8)

Substitutionof(8)in(7)yields:

(9)

2 Solutions of Riabouchinsky flows

2.1 solution of the type ψ=yξ(x,t)

We consider the plane unsteady flow and examine the solution of (9) of the form:

ψ=yξ(x,t)

(10)

whereξ(x,t)isanarbitraryfunctionofthevariablesx,t.Substituting(10)in(9),weobtainthefollowingequation

ξxxt-ξxξxx+ξξxxx-ν1ξxxxx+ν2ξxxxxxx=0

(11)

inwhichthesubscriptsindicatethederivativeswithrespecttothevariablesx,t.

Letusconsideraparticularsolutionof(11)oftheform

ξ(x,t)=-V+F(x+Vt)=-V+F(s)

(12)

whereVisaconstantandFsatisfiesthedifferentialequation

FF‴-F′F″-ν1F(4)+ν2F(6)=0

(13)

Forthesolutionoftheequation(13)wewrite

F(s)=δ(1+λeσs)

(14)

inwhichδ,λ,σarearbitraryrealconstants.Makinguseof(14)into(13),wehave

δ=ν1σ-ν2σ3

(15)

Thusthestreamfunctionwillbe

ψ=y[-V+(ν1σ-ν2σ3)(1+λeσ(x+Vt))]

(16)

Thevelocitycomponentsbecome

u(x,y,t)=-V+(ν1σ-ν2σ3)(1+λeσ(x+Vt))

(17)

v(x,y,t)=-λy(ν1σ2-ν2σ4)eσ(x+Vt))

(18)

Thestreamlineflowforψ=Ω1isgivenbythefunctionalform

(19)

Inaddition,whenV=0,thesolutionreducestosteadystatesolution,i.e.ψ=y(ν1σ-ν2σ3)(1+λeσ(x))

u(x,y,t)=(ν1σ-ν2σ3)(1+λeσ(x))

(20)

v(x,y,t)=-λy(ν1σ2-ν2σ4)eσ(x)

(21)

Thestreamlineflowforψ=Ω1isgivenbythefunctionalform

(22)

Weconsideranothersolutionofthetype

ψ=yξ(x,t)+η(x,t)

(23)

Substitutionof(23)intoequation(9)gives

yξxxt+ηxxt-(yξx+ηx)ξxx+ξ(yξxxx+ηxxx)-ν1(yξxxxx+ηxxxx)+ν2(yξxxxxxx+ηxxxxxx)=0.(24)

Fromtheaboveequationweobtainthefollowingdifferentialequationssatisfiedbyξandη.

ξxxt-ξxξxx+ξξxxx-ν1ξxxxx+ν2ξxxxxxx=0

(25)

ηxxt-ηxξxx+ξηxxx-ν1ηxxxx+ν2ηxxxxxx=0

(26)

Weobservethatthedifferentialequation(25)forξisthesameastheequation(11)whichsolutionisgivenin(12), (14)and(15).Inaddition,aparticularsolutionof(26)isη=ξ(x,t)andthisfactisusefulforthepurposeofpursuingfurthersolutions.Inparticular,ifξisgivenin(12), (14)and(15),wealsoconsidertheformofη

η=-V+G(x+Vt)=-V+G(s)

(27)

Insertingthesolutionofξand(27)intoequation(26),weget

-λ(ν1σ3-ν2σ5)eσsK(s)+(ν1σ-ν2σ3)(1+λeσs)K″(s)-ν1K‴(s)+ν2K(5)(s)=0

(28)

whereK(s)=G′(s).Itisnotedthatthedifferentialequation(28)forKisalinearordinarydifferentialequation.Itisnoteasytoobtainthegeneralsolution,soweconsiderthefollowingspecialcases:

Case 1. whenν1σ-ν2σ3=0, (28)reducesto

-ν1K‴(s)+ν2K(5)(s)=0

(29)

Thesolutionofaboveequationis

(30)

Weonlyconsiderν1ν2>0.ThenG(s)willbe

(31)

(32)

(33)

u(x,y,t)=-V

(34)

Thestreamlineflowforψ=Ω2isgivenbythefunctionalform

(35)

Figure2demonstratesthestreamlinespatternof(32)forV=1,ν1=0.3,ν2=0.4,t=1andb0=b2=b4=0,b1=b3=1.Ifν2=0,thefluidreducestoaNewtonianfluid.Thenwecangetσ=0andψ=-V-Vy+b0+b1(x+Vt)+b2(x+Vt)2+b3(x+Vt)3.AssumingagainthatV=0,weobtainasteadygeneralsolution.

ψ=b0+b1x+b2x+b3x

(36)

u(x,y)=0

(37)

v(x,y)=-b1-2b2x-3b3x

(38)

Ifb3≠0,itrepresentsthestreamlinesofPoiseuilleflows.Ifb3=0,b2≠0,itdenotestheSimpleCouetteflowswhosevelocityprofileislinearfunctionofx.Figure3representsthesimpleparallelCouetteflowof(36)forb0=-9,b1=-1,b2=10,b3=0anditiscomposedbyparallellines.

Case 2. whenσ=1andλ=0, (28)reducesto

(ν1-ν2)K″(s)-ν1K‴(s)+ν2K(5)(s)=0

(39)

Thesolutionofaboveequationis

(40)

(41)

(44)

Thestreamlineflowforψ=Ω3isgivenbythefunctionalform

Figure4demonstratesthestreamlinespatternof(42)forV=1,ν1=0.3,ν2=0.4,σ=1,t=1andd0=d1=d2=d5=0,d3=d4=1.

3 Conclusions

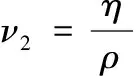
[1] STOKES V K. Couple stress in fluid[J]. The physics of fluids, 1966,9:1709-1715.

[2] HAYAT T, MUSTAFA M, IQBAL Z, ALSAEDI A. Stagnation-point flow of couple stress fluid with melting heat transfer[J]. Applied Mathematics and Mechanics (English Edition), 2013,34(2):167-176.

[3] HADJESFANDIARI A R, HAJESFANDIARI A, DARGUSH G F. Skew symmetric couple-stress fluid mechanics[J]. Acta Mechanica, 2015,226:871-895.

[4] RAMESH K, DEVAKAR M. Effects of heat and mass transfer on the peristaltic transport of MHD couple stress fluid through porous medium in a vertical asymmetric channel[J]. Journal of Fluids, 2015,163832.

[5] ZHANG D X, FENG S X, LU Z M, LIU Y L.Exact solutions for steady flow of second-grad fluid[J]. Journal of Shanghai University(English Edition), 2009,13(4):340-344.

[6] NEMENYI P F. Recent developments in inverse and semi-inverse methods in the mechanics of continua[J]. Advances in Applied Mechanics, 1951,2(11):123-151.

[7] HUI W H, Exact solutions of the 2-dim navier-stokes equations[J]. J Appl Math Phys ZAMP, 1987,38(5):689-702.

[8] LABROPULU F. A few more exact solutions of a second grade fluid via inverse method[J]. Mechanics Research Communications, 2000,27(6):713-720.

[9] ZHANG D X, SHI L R. Exact solutions of couple stress fluids, Chinese Quarterly of Mechanics, 2010,31(2):159164.

[10] Riabouchinsky D. Some considerations regarding plane irrotational motion of a liquid[J]. Compt Rend Hebd Seanc Acad Sci(Paris), 1924,179:1133-1136.

[11] ALSAEDI A, ALI N, TRIPATHI D, HAYAT T. Peristaltic flow of couple stress fluid through uniform porous medium, Applied Mathematics and Mechanics(English Edition), 2014,35(4):469-480.

[12] HAYAT T, MOHYUDDIN M R, ASGHAR S. Some inverse solutions for unsteanian fluid[J]. Tamsui Oxford Journal of Mathematical Sciences, 2005,21(1):1-20.

张道祥，程航.偶应力流体的Riabouchinsky型精确解[J].安徽师范大学学报：自然科学版，2015，38(5)：414-418.

偶应力流体的Riabouchinsky型精确解

张道祥， 程 航

(安徽师范大学 数学计算机科学学院，安徽 芜湖 241000)

本文目的是研究时间依赖的Riabouchinsky型偶应力流体的精确解.通过预设流函数的特定形式，我们获得了流体运动的定常和非定常解.结果表明，偶应力流体的速度场强烈地依赖于流体的物质参数.

偶应力流体；牛顿流体；Riabouchinsky流

10.14182/J.cnki.1001-2443.2015.05.002

date:2014-09-03

Supported by National Nature Science Foundation of China(10302002);the Foundation of Outstanding Young Talent in University of Anhui Province of China(2011SQRL022ZD).

Biography: Daoxiang Zhang(1979-), male, born at Tianchang, Anhui, associate professor, major in stability of differential equations and fluid mechanics.