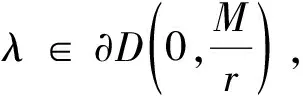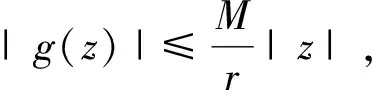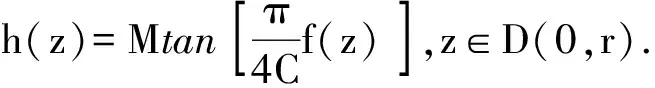Schwarz引理的推广及其应用
2014-09-17黄华平
黄华平
(湖北师范学院 数学与统计学院,湖北 黄石 435002)
1 引 言
Schwarz引理是解析函数的重要定理,它对共形映射的建立,特别是对著名的Riemann映照定理的论证,起了很大作用. 它揭示出经典解析映照后,由原像区域到像区域之间的有趣变化,给出了由给定区域来确定对象区域的有效估计.
在正文开始之前,先给出如下记号.
记D(z0,r)={z:|z-z0| 下面首先阐述Schwarz引理: 设f(z)∈H(D(0,1)), |f(z)|≤1(z∈D(0,1), 且f(0)=0, 则 (i) |f(z)|≤|z|,z∈D(0,1); (ii) |f′(0)|≤1; (iii) 若对某点0≠z0∈D(0,1),(i)或(ii)取等号,则∃λ∈∂D(0,1), 使得f(z)=λz. Schwarz引理在解析函数论,几何函数论,多元复分析等诸多领域中都应用很广. 例如,用它来证明Liouville定理(即有界整函数必为常数)非常方便. 如下: 设f(z)在z平面上解析,且|f(z)|≤M(M>0是一个常数). ∀r>0, 作辅助函数 则g(w)满足Schwarz引理的条件. 遂由Schwarz引理,|g(w)|≤|w|,w∈D(0,1). 故 上式令r→∞, 即得f(z)=f(0)恒为常数. 上述用Schwarz引理证明Liouville定理避免了通常的采用Cauchy不等式的证法[1],从而简洁明了. 近些年来,关于Schwarz引理的推广,已经涌现出了许多杰出的工作,并且还出现了大量的应用[2-8]. 本文主要给出了Schwarz引理一种最常见的推广形式的新证法,然后给出了两个定理阐述了此推广形式的应用. 首先引入Schwarz引理一个最常见的推广形式,这种推广形式文献[4-8]都有,并且也有证明,但证明过程或者不详细或者不完整. 本文给出了一种比较完整的新证法. 见如下引理1. 其次给出了一个常用性质,本文也以引理形式给出,见如下引理2,同时给出了证明. 另外,还给出了两个结论说明了其应用. 引理1设f(z)∈H(D(0,r)), |f(z)|≤M(z∈D(0,r)), 且f(0)=0, 则 证令 则g(z)∈H(D(0,r)). 事实上,只需证g(z)在z=0处可导即可. 如下: 利用复变函数的L ′Hospital法则,有 故g(z)在z=0处可导,从而g(z)∈H(D(0,r)). 对g(z)在D(0,r-ε)={z∶|z| 上面引理显然大大的推广了Schwarz引理. 事实上,在引理1中取r=M=1即可. 下面的性质经常用到,本文以引理形式给出. 证(i) 设z=x+iy, 则Rez=x, 从而 (e-ycosx+1)2-(e-ycosx-1)2=4e-ycosx≥0. 进而(e-ycosx+1)2≥(e-ycosx-1)2, 导出 (ii) 由于 (2.1) 故 (2.2) 并且 (2.3) 定理1设f(z)∈H(D(0,r)), 且f(0)=0. 若Ref(z)≤C(z∈D(0,r)),C>0为常数,则 证取M>0, 令 则g(z)∈H(D(0,r)), 且|g(z)|≤M(z∈D(0,r)). 事实上,因u=Ref(z)≤C(C>0), 所以2C-f(z)=(2C-u)-iv≠0. 否则有2C-u=0, 从而由2C=u≤C得到C≤0, 矛盾. 再由f(z)∈H(D(0,r))可得g(z)∈H(D(0,r)). 而由(2C-u)2≥u2得到 即得 定理2设f(z)∈H(D(0,r)), 且f(0)=0. 若|Ref(z)|≤C(z∈D(0,r)),C>0为常数,则 证令f(z)=u(x,y)+iv(x,y). 若|Ref(z)|=C(z∈D(0,r)), 则u=±C. 由于f(z)∈H(D(0,r)), 故由解析函数的Cauchy-Riemann方程易得v为常数,于是f(z)在D(0,r)内恒为常数. 又f(0)=0, 进而f(z)≡0(z∈D(0,r)). 此时定理得证. 下设|Ref(z)| 则g(z)∈H(D(0,r)), 且|g(z)|≤M(z∈D(0,r)). 事实上,由于 由于g(0)=0, 故由引理1, (2.4) (2.5) 又由 利用(2.5)式,有 再次利用(2.5)式,有 于是证得(ii). (2.6) 注意到 (2.7) 由(2.5), (2.6), (2.7)式可得 证得(iv). 而 因此由引理2 (ii)得到 即得 证得(iii). 注意,定理2中的(ii)实际上可由(iv)直接得出,这是因为|Imf(z)|≤|f(z)|对任意复变函数f(z)都成立. 定理2从本质上给出了开圆盘内满足假设条件的解析函数的实部,虚部以及模的估计式. [参 考 文 献] [1] 钟玉泉. 复变函数论 [M].3版. 北京: 高等教育出版社,2004. [2] Walter Rudin.Real and complex analysis[M]. Third edition.Beijing: China Machine Press,2004. [3] 邓冠铁. 复分析[M].北京: 北京师范大学出版社,2010. [4] 马晟,杨溪. 有关Schwarz引理的一个注记[J]. 黄冈师范学院学报,2010,30(6):17-18. [5] 何重月. 对Schwarz引理的探讨[J]. 娄底师专学报,1995,2:4-7. [6] 邹中柱. Schwarz引理在复变函数教学中的应用[J]. 怀化师专学报(自然科学版),1987,1:43-46. [7] 黄裕民. Schwarz引理的一些推广[J]. 零陵师专学报,1982,1:63-69. [8] 邵敏娟. Schwarz引理的几点推广[J]. 苏州铁道师院自然科学学报,1985,1:12-15.2 主要结果