谭尚旺,王东方,魏宁宁

(中国石油大学理学院,山东青岛266580)

1 问题的提出

本文中讨论的图都是无环和无重边的简单图，未定义的记号和术语见文献[1]。令G是顶点集和边集分别为V(G)和E(G)的一个连通图。G的1度点称为G的叶或悬挂点，关联叶的边称为G的悬挂边，两个不同顶点u和v之间的距离dG(u，v)就是G中连接这两个顶点的最短路的边数。为了方便，记dG(u，u)=0。对顶点v∈V(G)，令W(G，v)表示v与G中所有其它顶点之间距离的和，degG(v)表示v在G中的度，并且NG(v)表示v在G中的所有邻接顶点的集合。

连通图G的维纳指标W(G)定义为G中所有不同顶点对之间距离的和，即

图的维纳指标是基于距离的一个不变量，是与分子分支密切相关的最古老的拓扑指标之一，是化学家维纳在1947年设计和研究之后命名的[2-4]。维纳指标的许多化学应用是用来处理非循环的有机分子，其中这些有机分子的图是树。目前，维纳指标已经取得了许多结论，关于维纳指标的综述和维纳指标的化学应用及数学文献见[5]～[10]及其引用的文献。

Entringer等[11]证明了路Pn是所有n点树中具有最大维纳指标的唯一图，而星Sn是所有n点树中具有最小维纳指标的唯一图。Deng[11]确定了顶点数n≥9的所有化学树中维纳指标具有第一最大值到第十七最大值的所有树。Dong和 Guo[7]确定了所有n点树中维纳指标具有第一最小值到第十五最小值的所有树。Wang和Guo[12]确定了给定顶点数和直径的所有树中维纳指标最小的树。Fishermann等[13]和Rada[14]分别独立地确定了给定顶点数和最大度的所有树中维纳指标最小的树。令π=(d1，d2，…dn)是满足d1≥d2≥…≥dn的一个非负整数序列，如果π是某个简单连通图的顶点度序列，则称π是可图的。Zhang等[15]提出了下述问题：对给定的一个可图序列π，令

Γ(π)={G：G连通并且π是G的度序列}，求Γ(π)中所有图的维纳指标的上(下)界并且刻划达到上(下)界的所有极图。

Zhang等[15]研究了上述问题的一个特殊类，即对给定的树的一个度序列，刻划了具有最小维纳指标的极图，也确定了给定最大度、叶数或匹配数的所有树中具有最小维纳指标的极图。对上述问题，Zhang等[16]也研究了给定度序列的所有树中具有最大维纳指标的极图。Székely和Wang[17]确定了具有最大子树个数的二元树。

一个树称为毛毛虫图，如果从这个树中删去所有的叶后产生一个路。对一些图类，尽管已经发现了改变图的维纳指标的一些变换和寻求具有最小或最大维纳指标极图的一些方法[13-17]，但这些变换和方法在求给定度序列的毛毛虫图中具有最小维纳指标的极图时是无效的。本文的动机来源于上述结论，尤其是文献[15]提出的上述问题，本文中刻划了给定度序列的所有毛毛虫图中具有最小维纳指标的极图。

2 图的两个变换

给出图的两个变换并确定计算新图维纳指标的公式，用来确定具有最小维纳指标的极端毛毛虫图。

引理1[18]令u是连通图G的一个割点，G1和G2是G的两个连通子图。如果V(G1)∩V(G2)={u} 且G1∪G2=G，则。

引理2[5]令uv是连通图G的一个割边，G1和G2是G-uv中分别包含u和v的两个分支。记，则W(G)=W(G1)+W(G2)+n1W(G2，v)+n2W(G1，u)+n1n2。

定理1令u是连通图G的一个割点，G1和G2是G的两个连通子图并且V(G1)∩V(G2)={u}，G1∪G2=G，NG1(u)={u1，u2，…，us}。对G2中不同于u的另外一个点v，记G′=G-{uu1，uu2，…，uus}+{vu1，vu2，…，vus}，，则

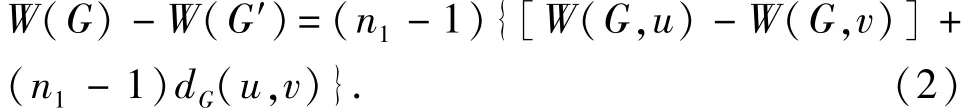
特别地，如果W(G，u)≥W(G，v)，则W(G)＞W(G′)。

证明令G′1=G1-{uu1，uu2，…，uus}+{vu1，vu2，…，vus}，则

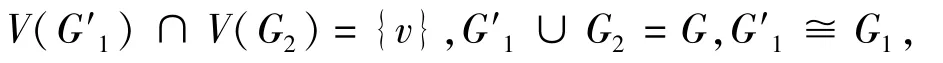
其中G′1的顶点v是G′的割点，且它对应G1的顶点u。因此，得

由于dG2(u，v)=dG(u，v)，于是由式(3) 和(4) 得到式(2)。此外，由式(2)附加断言显然成立。定理证毕。

定理2令u、v、a、b是连通图G的4个顶点且uv，ab∈E(G)，ua，vb∉E(G)。记k=dG(v，a)，G′=G-{uv，ab}+{ua，vb}(图1)。如果uv和ab都是G的割边，则

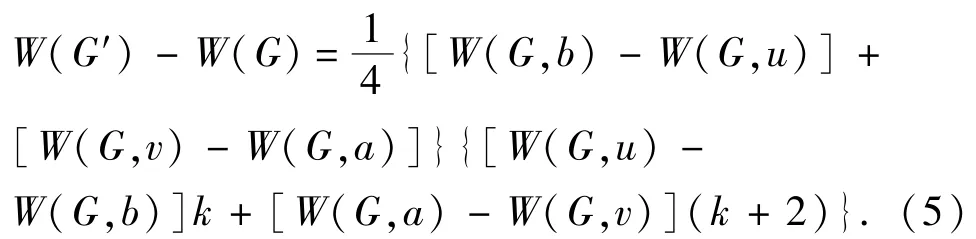
图1 定理2中从G到G′的图Fig.1 Diagrams from G to G′in theorem 2

证明令G1、G2和G3是G-uv-ab中分别包含顶点u，v和b的3个分支，Q是G-uv中包含顶点v的分支。记。

取G的割边uv和Q的割边ab分别作为引理2中的边uv，由引理2得

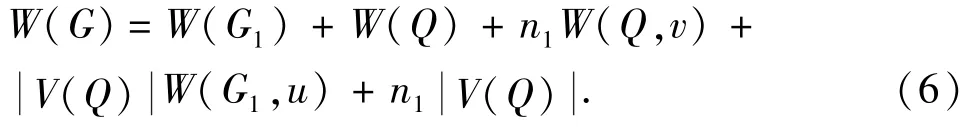
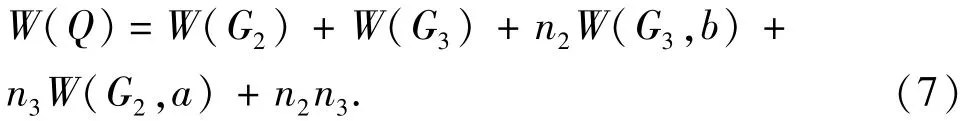
由W(G，u)的定义和G的假设得

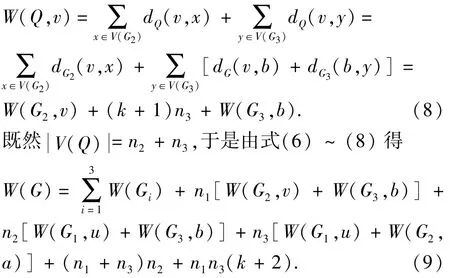
通过交换式(9)的v和a，得

于是由式(12)和(13)得

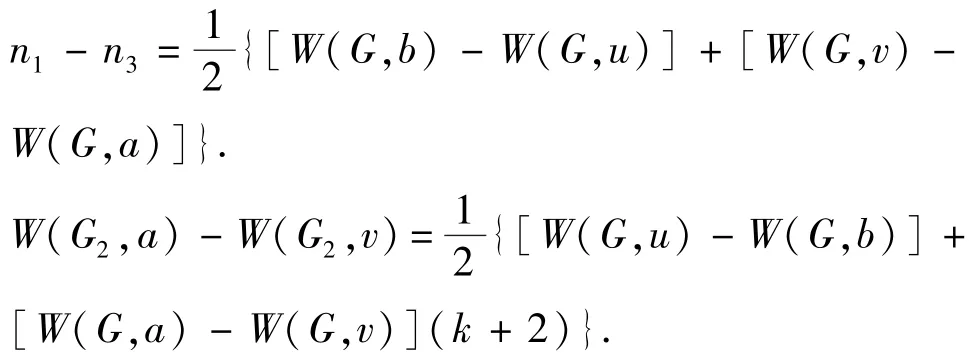
因此，由式(11)得到式(5)。定理证毕。

3 给定度序列的毛毛虫图中具有最小维纳指标的图

确定给定度序列的毛毛虫图中具有最小维纳指标的极图。

令Pd=v0v1…vd是直径为d的路。熟知，任一个直径为d的树T都能通过在Pd的顶点vi(i=2，3，…，d-1)上悬挂适当的树Ti而得到。令C(s1，s2，…，sd-1)表示通过在Pd的顶点vi(i=2，3，…，d-1)上增加个悬挂边得到的毛毛虫图。Wang和Guo[12]已经证明

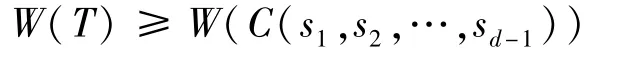
等式成立，当且仅当T≅C(s1，s2，…，sd-1)。

基于上述结论，令C(π)表示度序列为π的所有毛毛虫图的集合，其中π=(d1，d2，…，dn)，d1≥d2≥…≥ds≥2＞ds+1=…=dn=1。容易发现，C(π)中的所有毛毛虫图都有相同的直径d=1+s。令CM是C(π)中具有最小维纳指标的一个毛毛虫图。假设s≥3(否则，C(π)仅包含一个星图或双星图)，且假设d1，d2，…，dn中至少有两个是不同的(否则，n=1或2，问题是平凡的)。下面总假设PM=v0v1…vd是CM的一个最长路，研究CM的性质和结构。

引理3如果u和v都不是PM的叶并且W(CM，u) ≥W(CM，v)，则

证明假设degCM(u)＞degCM(v)。既然v不是PM的悬挂点，于是

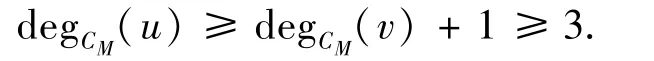
这表明在顶点u处存在一个不包含在PM上的悬挂边。令s=degCM(u)-degCM(v)，uu1，uu2，…，uus是CM中顶点u处不包含在PM上的s个悬挂边。记T′=CM-{uu1，uu2，…，uus}+{vu1，vu2，…，vus}，则T′∈C(π)。由定理1得W(T′)＜W(CM)，这与CM的假设矛盾。引理证毕。

引理4如果u是PM的一个悬挂点并且v不是PM的悬挂点，则

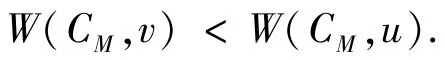
证明假设W(CM，v)≥W(CM，u)。不妨设u=v0并且v=vi(1≤i≤d-1)。记

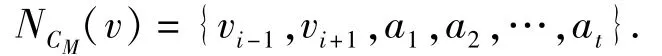
令T′=CM-{vivi+1，via1，via2，…，viat} +{v0vi+1，v0a1，v0a2，…，v0at}，则T′∈C(π)。由定理 1 得W(T′)＜W(CM)，这与CM的假设矛盾。引理证毕。

引理5令u、v、a、b是PM上依次从左到右的4个不同顶点，其中uv和ab是PM的两个边。记k=dCM(v，a)，则

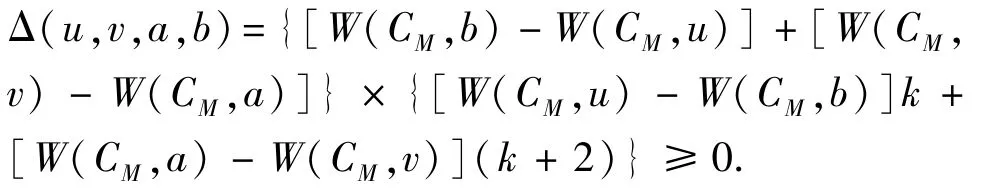
证明假设 Δ(u，v，a，b)＜0。令

这与CM的假设矛盾。引理证毕。

引理6如果存在非负整数0≤p＜q≤d，使W(CM，vp)=W(CM，vq)，则

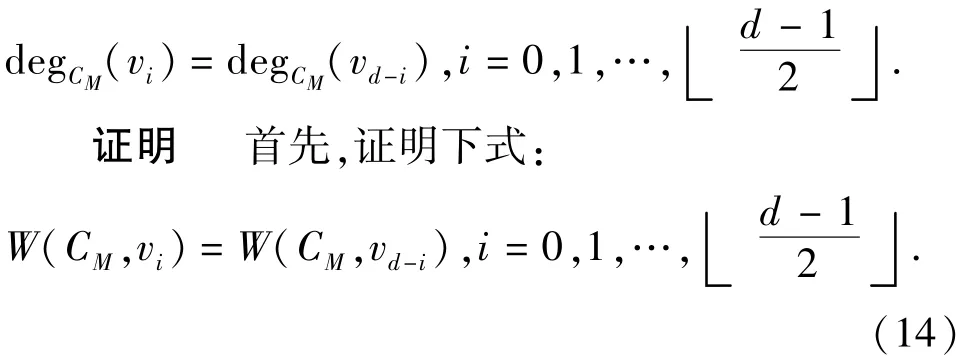
假 设W(CM，vp+1) ≠W(CM，vq-1)，不 妨 设W(CM，vp+1)＜W(CM，vq-1)。考虑PM上的4个不同顶点：u=vp，v=vp+1，a=vq-1，b=vq，容易发现 Δ(u，v，a，b)=[W(CM，v)-W(CM，a)][W(CM，a)-W(CM，v)](k+2)＜0.这与引理5的结论矛盾。因此，W(CM，vp+1)=W(CM，vq-1)。用p+1 和q-1分别代替上面的p和q，重复上述过程可得

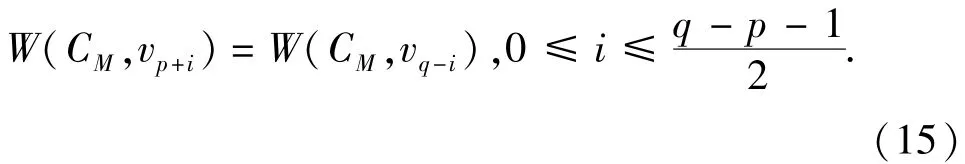
假 设W(CM，vp-1) ≠W(CM，vq+1)，不 妨 设W(CM，vp-1)＞W(CM，vq+1)。考虑PM上的4个不同顶点：u=vp-1，v=vp，a=vq，b=vq+1。容易发现

这与引理 5的结论矛盾。因此，W(CM，vp-1)=W(CM，vq+1)。用p-1和q+1分别代替上面的p和q，重复上述过程可得

假设p≠d-q，不妨设p＜d-q。由p+q＜d知，v0是PM的一个悬挂点，而vp+q是PM的非悬挂点。在式(16)中取i=p，得W(CM，v0)=W(CM，vp+q)，这与引理4的结论矛盾。因此，得到

由式(15)～(17)得到式(14)。

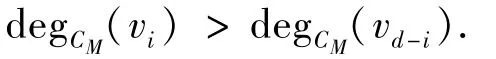
由式(14) 得W(CM，vi) ≥W(CM，vd-i)，于是由引理3得degCM(vi)≤degCM(vd-i)，这与假设矛盾。引理证毕。

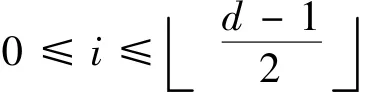
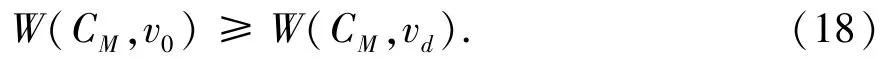
引理7 (1)如果d=2s是一个偶数，则

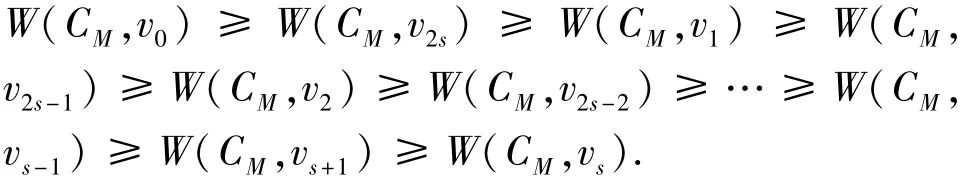
(2)如果d=2s+1是一个奇数，则

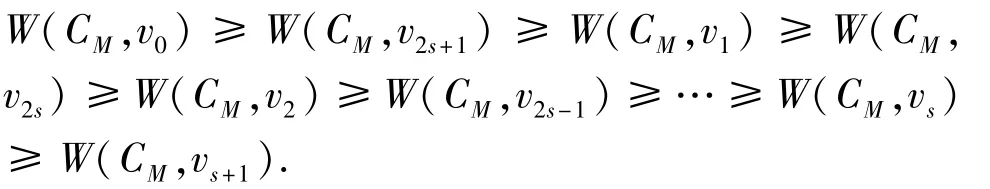
证明首先证明(1)。由式(18)和引理4得

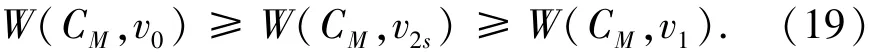
对1≤i≤s-1，根据式(19)，假设已经知道W(CM，v0) ≥W(CM，v2s) ≥ … ≥W(CM，vi-1) ≥W(CM，v2s-i+1) ≥W(CM，vi).

下面证明W(CM，vi)≥W(CM，v2s-i)。如果W(CM，vi)＜W(CM，v2s-i)，则考虑PM的4个不同顶点：u=vi-1，v=vi，a=v2s-i，b=v2s-i+1。既然

z(CM，u) ≥W(CM，b)，W(CM，v)＜W(CM，a)，于是Δ(u，v，a，b)＜0，与引理5的结论矛盾。因此，W(CM，vi)≥W(CM，v2s-i)。上述结论也表明

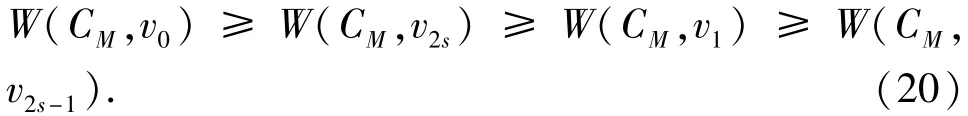
对1≤j≤s-2，根据式(20)，假设已知

下面证明W(CM，v2s-j)≥W(CM，vj+1)。如果W(CM，v2s-j)＜W(CM，vj+1)，则考虑PM的4 个不同顶点：u=v2s-j+1，v=v2s-j，a=vj+1，b=vj。既然W(CM，u) ≥W(CM，b)，W(CM，v)＜W(CM，a)，于是Δ(u，v，a，b)＜0，与引理5的结论矛盾。因此，W(CM，v2s-j) ≥W(CM，vj+1)。

由上述两方面的讨论和归纳法原理，完成了(1)的证明。

(2)的证明与(1)的证明类似。

假设式(18)成立，即W(CM，v0)≥W(CM，vd)。记degCM(v)=deg(v)，则由引理3和引理7，当d=2s时，

当d=2s+1时，

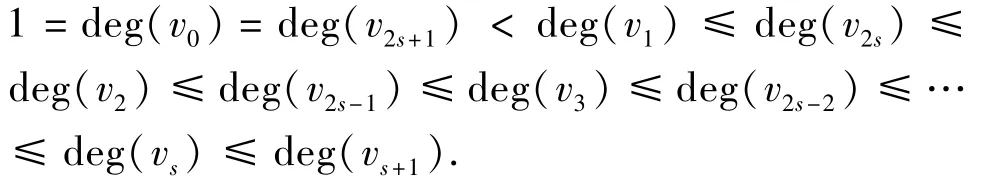
这表明，对给定的树的一个度序列π=(d1，d2，…，dn)，图CM是唯一确定的。因此，得到下面的结论。

定理3对给定的树的任一个度序列π，CM是C(π)中具有最小维纳指标的唯一图。

图2和图3分别显示了两个具有最小维纳指标的毛毛虫图，其中

特别地，图3显示的毛毛虫图是对称的。

图2 C(π1)中具有最小维纳指标的毛毛虫图Fig.2 Caterpillar with the smallest Wiener index in C(π1)

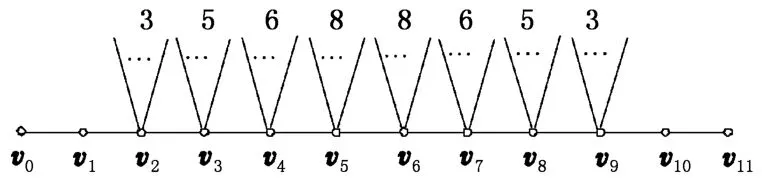
图3 C(π2)中具有最小维纳指标的毛毛虫图Fig.3 Caterpillar with the smallest Wiener index in C(π2)

[1] BONDY J A，MURTY U S R.Graph theory with applications[M].New York：Macmillan Press，1976.

[2] WIENER H.Structural determination of paraffin boiling points[J].J Am Chem Soc，1947，69：17-20.

[3] HOSOYA H.Topological index：a newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons[J].Bull Chem Soc Jpn，1971，44：2332-2339.

[4] TODESCHINI R，CONSONNI V.Handbook of Molecular Descriptors[M].Weinheim：Wiley-VCH Press，2000.

[5] DOBRYNIN A A，ENTRINGER R，GUTMAN I.Wiener index of trees：theory and applications[J].Acta Appl Math，2001，66：211-249.

[6] DENG H.The trees onn≥9 vertices with the first to seventeenth largest Wiener indices are chemical trees[J].MATCH Commun Math Comput Chem，2007，57：393-402.

[7] DONG H，GUO X.Ordering trees by their Wiener indices[J].MATCH Commun Math Comput Chem，2006，56：527-540.

[8] GUTMAN I，YEH Y N，LEE S L，et al.Wiener numbers of dendrimers[J].MATCH Commun Math Comput Chem，1994，30：103-115.

[9] XU K，TRINAJSTIC N.Hyper-Wiener and Harary indices of graphs with cut edges[J].Util Math，2011，84：153-163.

[10] DIUDEA M V，KATONA G，MINAILIUC O M，et al.Wiener and hyper-Wiener indices in spiro-graphs[J].Russ Chem Bull，1995，44：1601-1611.

[11] ENTRINGER R C，JACKSON D E，SYNDER D A.Distance in graphs[J].Czechoslovak Math J，1976，26：283-296.

[12] WANG S J，GUO X F.Trees with extremal Wiener indices[J].MATCH Commun Math Comput Chem，2008，60：609-622.

[13] FISHERMANN M，HOFFMANN A，RAUTENBACH D，et al.Wiener index versus maximum degree in trees[J].Disc Appl Math，2002，122：127-137.

[14] RADA J.Variation of the Wiener index under tree transformations[J].Disc Appl Math，2005，148：135-146.

[15] ZHANG X D，XIANG Q Y，XU L Q，et al.The Wiener index of trees with given degree sequences[J].MATCH Commun Math Comput Chem，2008，60：623-644.

[16] ZHANG X D，LIU Y，HAN M X.Maximum Wiener index of trees with given degree sequence[J].MATCH Commun Math Comput Chem，2010，64：661-682.

[17] SZEKELY L A，WANG H.Binary trees with the largest number of subtrees[J].Discr Appl Math，2007，155：374-385.

[18] BALAKRISHNAN R，SRIDHARAN N，VISWANATHAN Iyer K.Wiener index of graphs with more than one cutvertex[J].Appl Math Lett，2008，21：922-927.