余波

(玉溪师范学院 理学院,云南 玉溪 653100)

“问题变式”在高等代数考研复习中的应用①

余波

(玉溪师范学院 理学院,云南 玉溪 653100)

高等代数;考研复习;问题变式;问题解决

以问题变式的形式,例举出高等代数考研题中的几组变式题.其主要目的是要说明:学习者在进行解题训练时,首先应立足于课本,熟练掌握课本习题提供的解题思想和方法.其次,应多关注题与题之间的关系,从中抽取出问题表面特征以外的结构特征,进而找出解决问题的思路和方法.再次,是应学会对问题进行多层次变式分析(或构造).通过变式分析(或构造),可以对问题解决过程及问题本身的结构有一个清晰的认识.

将源问题加以变化得到的新问题,称为变式题;将源问题加以变化,称为问题变式[1].本文以问题变式的形式,例举出高等代数考研题中的几组变式题,并以此给出了考研复习的一点建议.

1 变式题组一

源题目设f1(x),f2(x)是复数域上的两个多项式,如果(x2+x+1)|f1(x3)+xf2(x3),那么(x-1)|f1(x),(x-1)|f2(x).(文献[2]第46页第25题)

证明因为x3-1=(x-1)(x2+x+1).

变式题1[3](上海交大)设fi(x)(i=1,2,3,4)是复数域上的多项式,若(x4+x3+x2+x+1) |[x3f1(x5)+x2f2(x5)+xf3(x5)+f4(x5)],求证:fi(1)=0(i=1,2,3,4).

由范德蒙行列式可知方程组的系数行列式不等于零,所以fi(1)=0(i=1,2,3,4)

由于方程组的系数行列式是个范德蒙行列式,由ε1,ε2,…,εn-1互不相同知它不为零,故方程组只有零解,于是

变式题3[4](上海大学)设f1(x),f2(x),…,fn-1(x)是n-1个(n≥2)复数域上的多项式,已知

证明由(x-1)|p(x),知(xn-1)|p(xn),且p(1)=0.

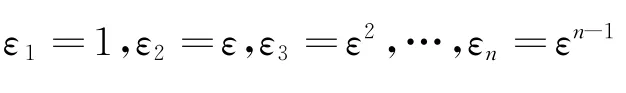
由于方程组的系数行列式是个范德蒙行列式,由ε1,ε2,…,εn互不相同知它不为零,故方程组只有零解,于是pi(1)=0(i=1,2,…,n-1).

每个数学问题可分解为表面形式特征和深层数学结构特征.在变式题组一中,问题呈现的内容逐步由简单到复杂,由具体到一般化,问题的表面形式特征发生了较大变化.但是,通过问题解决的过程,我们看到每个问题的深层数学结构却没有发生“质”的改变,即不同的问题重复做着同一件事情(同一过程,同一方法).因此,解决此类问题时,只需通过源问题就可以提供问题解决的正确方法.

2 变式题组二

源题目设V1,V2都是线性空间V的子空间,且V1⊂V2,证明:如果V1的维数与V2的维数相等,那么V1=V2.(文献[2]第269页第10题)

证明设V1的维数为r,α1,α2,…,αr是V1的一个基.因为V1⊂V2,故α1,α2,…,αr可以扩充成为V2的一个基.又因V1的维数与V2的维数相等,故α1,α2,…,αr也是V2的一个基,因此V1=V2.

变式题1[4](重庆大学)已知同维数的两个向量组有相同的秩,且其中之一可用另外一个线性表出,则这两个向量组等价.

证明设同维数的两个向量组分别为α1,α2,…,αs和β1,β2,…,βt,且它们有相同的秩,不妨设β1,β2,…,βt可由α1,α2,…,αs线性表出.令U=L(α1,α2,…,αs),V=L(β1,β2,…,βt),则V⊂U.又因α1,α2,…,αs和β1,β2,…,βt有相同的秩,所以V的维数与U的维数相等,从而V=U,即可得α1,α2,…,αs和β1,β2,…, βt等价.

变式题2[4](北京邮电大学)设Ax=0与Bx=0均为n元齐次线性方程组,r(A)=r(B),且方程组Ax=0的解为方程组Bx=0的解.则方程组Ax=0与Bx=0同解.

证明设W1,W2分别是Ax=0与Bx=0的解空间,因方程组Ax=0的解为方程组Bx=0的解,故W1⊂W2.又r(A)=r(B),故

维(W1)=n-r(A)=n-r(B)=维(W2)所以,(W1)=(W2),此即方程组Ax=0与Bx=0同解.

变式题3[3]设A,B都是n级方阵,若r(AB)=r(B),则方程组(AB)x=0与Bx=0同解.

证明设W1,W2分别是(AB)x=0与Bx=0的解空间.设β∈W2,则Bβ=0,从而(AB)β=A(Bβ) =A 0=0,故β∈W1,所以W2⊂W1.又r(AB)=r(B),故维(W1)=n-r(AB)=n-r(B)=维(W2)所以,W1=W2,此即方程组(AB)x=0与Bx=0同解.

故Pn=V1⊕V2.

维(W1+W2)=维(W1)+维(W2)-维(W1∩W2)=n-r(A)+n-r(B)=n-m+m=n=维(Pn)

故Pn=W1⊕W2.

问题变式分为水平变式和垂直变式.水平变式是指新问题相对源问题来说,学习者能区分问题表面形式特征变化背后的结构特征变化,不带来认知负荷的变化;垂直变式是指学习者不能区分问题表面形式特征变化背后的结构特征变化[1].

通过对变式题组二的变式分析,以及问题解决的过程,我们看到每个问题解决所涉及到的知识和方法虽然不一样,但是源问题提供的结论却是每一个问题解决的关键.即同一结论运用到不同的问题解决中(一题多变).

3 变式题组三

源题目设β1,β2,…,βs为s个线性无关的n维向量,则存在含有n个未知量的齐次线性方程组Ax= 0,使β1,β2,…,βs是它的一个基础解系.

解令B=(β1,β2,…,βs),则B是一个n×s的矩阵,若令Aβi=0(i=1,2,…,s),则AB=A(β1,β2,…,βs)=(Aβ1,Aβ2,…,Aβs)=0,两边取转置,即有B′A′=0.由此可知,所要构造的方程组Ax=0的系数矩阵A的行向量,应是线性方程组B′x=0的解向量.

该例给出了构造某一齐次线性方程组,使已知的一组线性无关的向量为其基础解系的方法.

变式题1已知线性方程组

的一个基础解系为:(b11,b12,…,b1,2n)′,(b21,b22,…,b2,2n)′,(bn1,bn2,…,bn,2n)′,试写出线性方程组

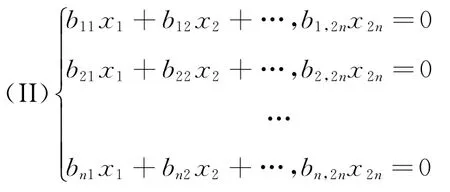
的通解.

解将方程组(I)与(II)用矩阵形式表示为Ax=0,Bx=0,其中A=(aij)n×2n,B=(bij)n×2n.由于B′的每一列都是(I)的解,所以AB′=0,两边取转置得BA′=0,可见A′的每一列都是(II)的解,又由于B′的列向量是(I)的基础解系,从而r(B)=r(B′)=n.又(I)的基础解系含2n-r(A)个解向量,故n=2nr(A),即r(A)=n,所以A′列向量线性无关.由于(II)的基础解系含2n-r(B)=2n-n=n个解向量,从而A′的列向量组是(II)的一个基础解系,故方程组(II)的通解为

其中k1,k2,…,kn为任意常数.

变式题2设Pn是数域P上全体n维向量组成的线性空间,则Pn的任一子空间W必至少是一个n元齐次线性方程组的解空间.

变式题3设β1,β2,…,βs是欧氏空间Rn(指定标准内积)中s个线性无关的向量,令U=L(β1,β2,…, βs),求U⊥的维数和一组基.

对于变式题1来说,表面形式特征没有发生变化,与源题目有相同的数学结构特征.根据源题目提供的构造方法,只需求出方程组(I)的系数矩阵的行向量组的一个极大线性无关组即可.因此它是源题目的水平变式.在变式题2中,涉及到线性空间、子空间、解空间等概念,问题的表面形式特征发生了变化,已不能较容易的区分对数学结构特征所带来的变化,增加了认知负荷,它是源题目的垂直变式.这时我们需明白齐次线性方程组的解空间与基础解系之间的关系,发现“变中的不变”,逐步提取与源题目提供的构造方法相同的数学结构元素,并利用其完成证明.在变式题3中,涉及到欧氏空间、内积、正交补等概念,问题的表面形式特征及深层次数学结构特征都发生了重大变化,认知负荷变化最大,它是源题目的垂直变式.

4 对考研复习的一点建议

⑴课本中的习题体现了某种解题思想和方法,具有基础性和示范性.文中的前两个变式题组是以课本中的习题为源问题这一事实,就足以能说明课本习题的重要性.因此,学习者在进行解题训练时,首先应立足于课本,熟练掌握课本习题提供的解题思想和方法,熟练掌握课本习题提供的结论.

⑵学习者在进行解题训练时,应多关注题与题之间的关系,从其不变的关系中抽取出问题表面特征以外的结构特征,不受问题表面特征的干扰,建立起题目的数学结构,进而把问题分类,使题目类型化.这样,学习者经过表面相似问题的解决,经过有变化的重复学习,可以形成一种心理定势,建立起此类问题的数学结构,进而找出解决问题的思路和方法.

⑶应学会对问题进行多层次变式分析(或构造).通过变式分析(或构造),可以对问题解决过程及问题本身的结构有一个清晰的认识,这是学习者积累问题解决经验、提高解决问题能力的一条有效途径[5].

[1]孙旭花,黄毅英,林智中,等.问题变式:结构与功能的统一[J].课程·教材·教法.2006,26(5):38-42.

[2]北京大学数学系几何与代数教研室前代数小组.高等代数[M].王萼芳,石生明,修订.北京:高等教育出版社,2003.

[3]徐仲,陆全,张凯院,等.高等代数考研教案[M].西安:西北工业大学出版社,2006.

[4]研究生入学考试试题研究组.研究生入学考试考点解析与真题详解——高等代数[M].北京:电子工业出版社,2008.

[5]鲍建生,黄荣金,易凌峰,等.变式教学研究[J].数学教学.2003(1～3):11-12,6-10,6-11.

Application of“Question Variations”in the Review of Advanced Algebra for Postgraduate Entrance Exams

YU Bo
(School of Science,Yuxi Normal University,Yuxi,Yunnan 653100,China)

advanced algebra;review for postgraduate entrance exams;question variations;problem solving

In this paper,the author tries to illustrate how to get learners acquainted with the problem solving process and the structure of problems in problem solving training with examples of variant questions appeared in the postgraduate entrance exam:first,learners should master the solving idea and method of the textbook problems;second,they should find out the structure features of problems from the superficial characteristics after analysis of relations between problems; third,learners should know how to construct a variant problem at different levels.

O15

A

1009-9506(2014)04-0007-06

2014年2月11日

余 波,硕士,讲师,研究方向:高等代数.

①教改项目:玉溪师范学院2013年教改项目,编号:201305.