陈斯养，黄晓宇

（陕西师范大学数学与信息科学学院，西安710062）

带有分段常数变量的微分方程是近年来引起广泛关注的一类泛函微分方程.这类方程是连续和离散变量的混合体，具有微分方程和差分方程的双重性质，在生态数学中具有重要的应用.文献［1］研究了具分段常数变量微分方程的全局吸引性，文献［2－4］讨论了具分段常数变量微分方程的振动及非振动性，文献［5－6］利用概周期型序列研究了具有分段常数变量微分方程的概周期解、渐近概周期解和伪概周期解的存在性和唯一性，文献［7］用中心流形理论分析了具有分段常数变量的捕食－被捕食模型的Flip分支、Hopf分支及Neimark－Sacker分支.

本文给出了具分段常数变量的时滞造血模型其中，P（t）表示血液循环过程中成熟干细胞的密度，l，m是骨髓中未成熟干细胞由产生到成为成熟干细胞所需时间，β，b，α，r均为正参数.

为了便于对模型（1）进行研究，在其等式两边同乘以ert，并分别在区间［n，t）上积分，整理可得

其中，t∈［n，n＋1）（n＝0，1，2，…），令t→n＋1，可得时滞差分方程模型

本文讨论模型（1）的等价模型（3）当1≤m≤l≤2时正平衡态的局部渐近稳定性，并对其Flip分支和Neimark－Sacker（以下均简写为N－S）分支进行分支分析.

1 正平衡态的存在性及局部稳定性

为了分析（3）正平衡态˜P的局部稳定性，令X（n）＝P（n）－，则（3）等价转化为：

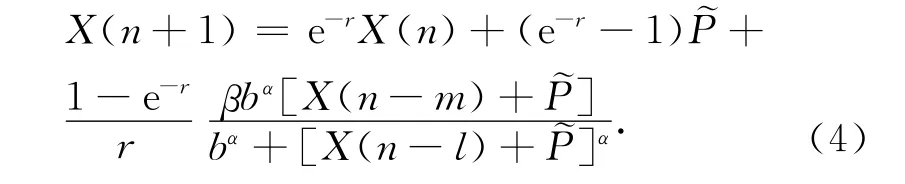
将（4）在X＝0处进行Taylor展开，可得其线性近似系统为：

由（5）得特征方程为：

由差分方程的稳定性理论可知，当且仅当所有的特征根满足｜λi｜＜1，i＝1，2，3，…，l＋1，正平衡态是局部渐近稳定的.

根据Jury判据［8］，可以得到以下关于正平衡态˜P局部渐近稳定的充要条件.

定理1对模型（3），以下结论成立：

（Ⅰ）当m＝l＝1时，˜P局部渐近稳定的充要条件为：

（Ⅱ）当m＝l＝2时，˜P局部渐近稳定的充要条件为：

（Ⅲ）当m＝1，l＝2时，

2 分支的存在性

由分支理论［9］可知，对应于特征值λ＝－1的分支称为Flip分支，对应于λ1，2＝e±iθ，0＜θ＜π的分支称为N－S分支.这一节，选取β0作为分支参数讨论（3）的Flip分支和N－S分支的存在性条件.

对于特征方程（6），记G（λ）＝λl＋1－e－rλl－（1

证明若定理条件成立，则G（λ）＝λ2－e－rλ＋1，此时，对于方程G（λ）＝0，求解可得其存在一对共轭复根且满足｜λ1，2｜＝1.故（3）在产生N－S分支.

证明若定理条件成立，则G（λ）＝λ3－e－rλ2－（）此时，方程Gλ＝0可分解为

且满足｜λ3｜＜1.故（3）在产生N－S分支.

证明若定理的条件①成立，则G（λ）＝λ3－e－rλ2－（1－e－r）λ＋2e－r，此时，方程G（λ）＝0因式分解为G（λ）＝（λ＋1）（λ2－（1＋e－r）λ＋2e－r），可得λ1＝－1，｜λ2，3｜＜1，故（3）在产生Flip分支；

若定理的条件②成立，则G（λ）＝λ3－e－rλ2－，此时，对方程G（λ）＝0作因式分解

注1当定理2、定理3的条件及定理4的条件②成立时，模型（3）不存在Flip分支；当定理4的条件①成立时，模型（3）不存在N－S分支.

3 分支的方向和稳定性

这一节利用文献［9］中的规范化理论和中心流形的计算方法研究和讨论了分支的方向及其稳定性.现将模型（3）等价转化为l＋1维差分方程组

为了研究（3）的分支方向及稳定性，需将（7）转化为ρ（n＋1）＝Uρ（n）＋Q（ρ（n））.其中，ρ（n）＝（P1，P2，…，Pm＋1，…，Pl＋1）∈Rl＋1，U为l＋1维方阵，Q（ρ）＝O（‖ρ‖2）是光滑函数，在ρ＝0处，Q（ρ）的Taylor展开为，其中E和F是多重线性函数，对平面向量x＝（x1，x2，…，xl＋1）T，y＝（y1，y2，…，yl＋1）T和z＝（z1，z2，…，zl＋1）T取值，在坐标下的分量分别为

其中，i＝1，2，3，…，l＋1.

3.1 当m＝l＝1，2时分支的方向和稳定性

当m＝l＝2时，（3）转化为等价差分方程组若定理3的条件成立，则模型（8）在正平衡态（，）T产生N－S分支.

作变量变换P1（n）＝＋ξ1（n），P2（n）＝＋ξ2（n），P3（n）＝＋ξ3（n），将（8）转化为

将（9）的第一个方程在ξ2（n）＝0进行Taylor展开，得到等价方程组

此系统可表示为：

其中

系统（10）在中心流形上的限制规范化方程为z（n＋1）＝eiθz（n）（1＋l｜z（n）｜2）＋O（｜z（n）｜4），其中，z（n）＝〈p1，ξ（n）〉，而l0＝Rel为N－S分支的临界规范形系数，决定了分支的方向及稳定性，且

当m＝l＝1时，若定理2的条件成立，则运用同样的方法可得N－S分支的临界规范形系数为：

定理5若定理2的条件成立，当l0、l1＜0（＞0）时，模型（3）存在唯一稳定（不稳定）的超（亚）临界的N－S分支.

3.2 当m＝1，l＝2时分支的方向和稳定性

当m＝1，l＝2时，（3）转化为等价差分方程组

将（12）的第一个方程在（ξ2（n），ξ3（n））＝（0，0）进行Taylor展开，得到等价方程组

此系统可表示为

其中，

而

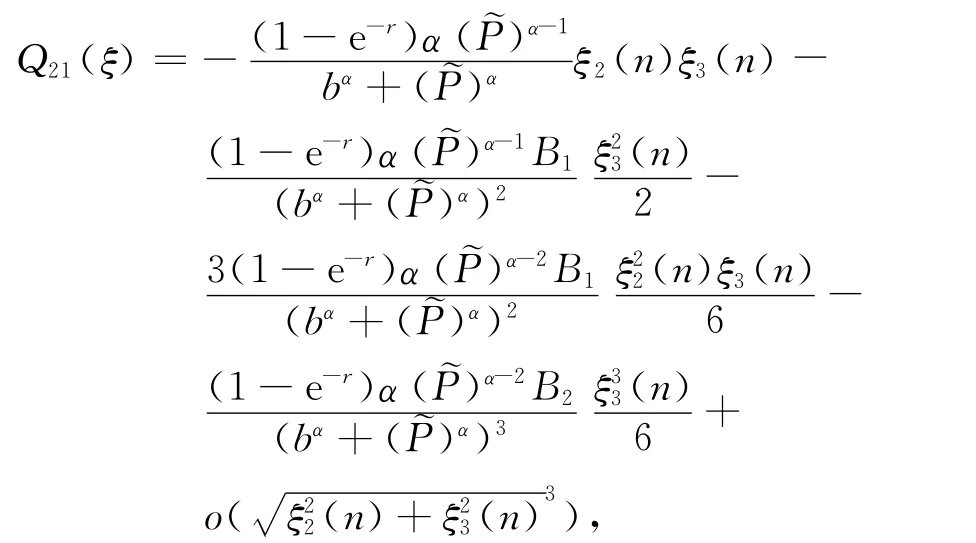
其中，B1＝（α－1）bα－（α＋1）（）α，B2＝（α2－3α＋2）b2α－4（α2－1）bα（）α＋（α2＋3α＋2）（）2α.

向量q2～（－1，1，－1）T，p2～分别为矩阵B0和的特征向量，即满足B0q2＝e，p2＝e－iθp2.为了使向量q2和p2满足〈p2，q2〉＝p21q21＋p22q22＋p23q23＝1，可取q2＝（－1，1，－1）T，p2＝.多重线性函数E和F分别取值为

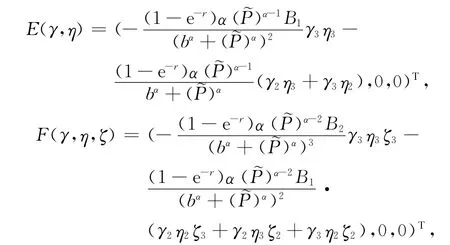
而

系统（13）在中心流形上的限制规范的化方程为ω（n＋1）＝－ω（n）＋d0ω3（n）＋O（ω4（n）），其中，ω（n）＝〈p2，ξ（n）〉，而d0为Flip分支的临界规范形系数，决定了Flip分支的方向及稳定性.计算得该系数为：

其中，

定理6若定理4的条件①成立，当d0＜0（＞0）时，模型（9）存在唯一稳定（不稳定）的、超（亚）临界的Flip分支.

若定理4的条件②成立，则模型（11）在正平衡态（˜P，˜P，˜P）T产生N－S分支.作变量变换以及利用Taylor展开公式，可得到系统（11）的等价方程组

此系统可表示为：

其中，

而

多重线性函数E和F分别取值为：

可计算得N－S分支的临界规范形系数为：

定理7若定理4的条件②成立，当l2＜0（＞0）时，模型（3）存在唯一稳定（不稳定）的、超（亚）临界的N－S分支.

4 数值模拟

这一部分对模型（3）进行了数值模拟，通过图形对模型（3）进行分支分析并体现了该生物系统复杂的动力学行为，如周期倍分和混沌现象等.下面通过实例验证文中所得定理与数值计算的一致性.

例1在模型（3）或其等价方程组（8）中取m＝l＝1，r＝0.5，b＝1，α＝4，根据定理2，可得分支参数的临界值为β0＝4.362，此时唯一的正平衡态为P＝1.6671.于是，当β＜β0时，P为局部渐近稳定的，当β＞β0时，P变为不稳定.在临界参数值β0，有特征值λ1，2＝e±iθ，0＜θ＜π，此时，N－S分支产生，见β－P分支图1.计算可得分支的临界规范形系数l1＜0，由定理5，可知当β＞β0时，从P分支出唯一稳定的N－S分支.

当β＝4.2＜β0时，P为局部渐近稳定的，此时，所有的解均趋于正平衡态P＝P1＝1.6493（见图2）；当β＝4.66＞β0时，在˜P＝˜P2＝1.6984产生N－S分支及分支周期解（见图3）.

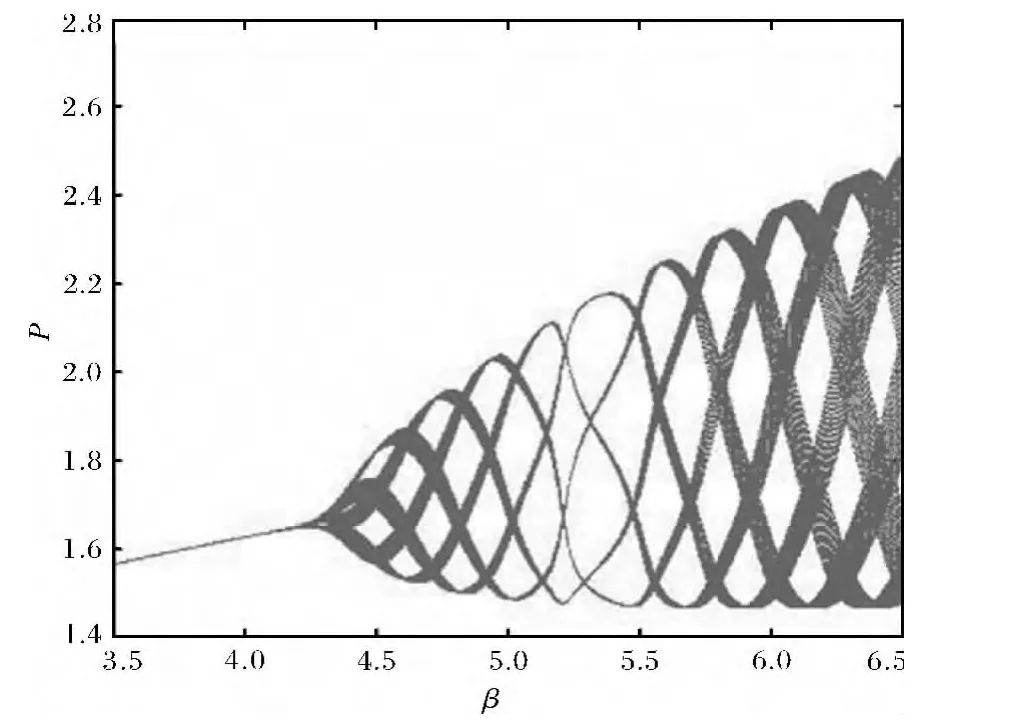
图1 β－P分支图Fig.1 Branch map about rand P

图2 稳定图（β＝4.2＜β0）Fig.2 Stability map（β＝4.2＜β0）

图3 N－S分支及周期解图（β＝4.66＞β0）Fig.3 Branch map of N－S and periodic solution（β＝4.66＞β0）

例2当m＝l＝2时，在模型（3）或其等价方程组（8）中取r＝3，b＝1，α＝3，根据定理3，可计算得分支参数的临界值为β0＝9.2452，此时，模型（3）存在唯一的正平衡态P＝1.2769.当β＜β0时，正平衡态为局部渐近稳定的，当β＞β0时，P变为不稳定.在临界参数值β0，有特征值λ1，2＝e±iθ，0＜θ＜π，此时，N－S分支产生，见β－P分支图4.计算可得分支的临界规范形系数l0＜0，由定理5，可知当β＞β0时，在产生唯一稳定的、超临界的N－S分支.

当β＝8.995＜β0时，＝＝1.2596为局部渐近稳定的（见图5）；当β＝9.44＞β0时，在正平衡态＝＝1.29产生N－S分支及分支周期解（见图6）.

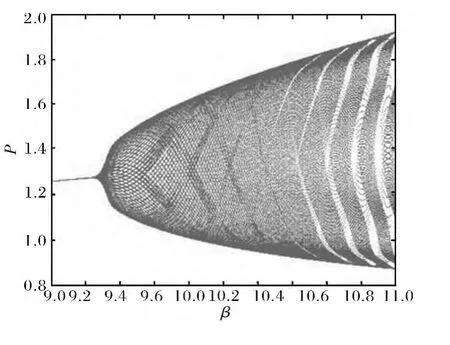
图4 β－P分支图Fig.4 Branch map about rand P

图5 稳定图（β＝8.995＜β0）Fig.5 Stability map（β＝8.995＜β0）

图6 N－S分支及周期解图（β＝9.44＞β0）Fig.6 Branch map of N－S and periodic solution（β＝9.44＞β0）

例3当m＝1，l＝2时，在模型（3）或其等价方程组（17）中取r＝0.5，b＝1，α＝3，根据定理4的条件②，可计算得分支参数的临界值为β0＝2.2281，此时，模型（9）唯一的正平衡态为˜P＝1.5119，对应的β－P分支图（见图7）.由图7可知，当β＜β0时，正平衡态为局部渐近稳定的，当β＞β0时，变为不稳定，在产生N－S分支.计算可得分支的临界规范形系数l2＜0，由定理7，可知当β＞β0时，在产生唯一稳定的N－S分支.

当β＝2.1＜β0时，＝＝1.4736为局部渐近稳定的（见图8）；当β＝2.4＞β0时，在正平衡态＝＝1.5605产生N－S分支及分支周期解（见图9）.

图7 β－P分支图Fig.7 Branch map about rand P

图8 稳定图（β＝2.1＜β0）Fig.8 Stability map（β＝2.1＜β0）

图9 N－S分支及周期解图（β＝2.4＞β0）Fig.9 Branch map of N－S and periodic solution（β＝2.4＞β0）

例4当m＝1，l＝2时，在模型（3）或其等价方程组（11）中取r＝1.5，b＝1，α＝1，根据定理4的条件①，可计算得分支参数的临界值为β0＝3.5247，唯一的正平衡态为P＊＝1.3498.于是，当β＜β0时，P＊为局部渐近稳定的，当β＞β0时，P＊变为不稳定.在临界参数值β＝β0，有特征值λ＝－1，此时Flip分支产生.计算分支的临界规范形系数可得d0＜0，由定理6，可知当β＞β0时，在P＊产生唯一稳定的Flip分支.

当β＝3.36＜β0时，P＊为局部渐近稳定的，此时P＊＝P7＊＝1.24（见图10）；当β＝3.68＞β0时，在P＊＝P8＊＝1.4533产生Flip分支及分支周期解（见图11）.

图10 稳定图（β＝3.36＜β0）Fig.10 Stability map（β＝3.36＜β0）

图11 Flip分支及周期解图（β＝3.68＞β0）Fig.11 Branch map of Flip and periodic solution（β＝3.68＞β0）

［1］ Wang Youbin，Yan Jurang.Necessary and Sufficient Condition for the Global Attractivity of the Trivial Solution of a Delay equation with Continuous and Piecewise Constant Arguments［J］.Appl Math.Lett，1997，10（5）：91－96.

［2］ Wang Youbin，Yan Jurang.Necessary and Sufficient Conditions for the Oscillation of a Delay Logistic equation with Continuous and Piecewise Constant Arguments［J］.Ann of Diff Eqs，2005，21（3）：435－438.

［3］ Shen J H，Stavroulakis I P.Oscillatory and Nonoscillatory Delay equations with Piecewise Constant Argument［J］.Journal of Mathematical Analysis and Applications，2000，248：385－401.

［4］ 王幼斌，燕居让.具逐段常变量时滞微分方程的振动性［J］.科学通报，1996，41（5）：393－395.

［5］ AIonso A I，Hong J L，Obay A R.Almost Periodic Type Solutions of Differential equations with Piecewise Constant Argument via Almost Periodic Type Sequences［J］.Appl Math Lett，2000，13：131－137.

［6］ 朴大雄.具逐段常变量的中立型时滞微分方程的伪概周期解［J］.北京大学学报：自然科学版，2001，37（3）：298－304.

［7］ 陈斯养，张 艳.具有分段常数变量的捕食—被捕食模型的分支分析［J］.兰州大学学报：自然科学版，2012，48（3）：104－112.

［8］ Mustafa R S K，Merino O.Discrete Dynamical Systems and Difference Equations with Mathematica［M］.New York：A CRC Press Company，2002.

［9］ Yuri A K.Elements of Applied Bifurcation Theory［M］.3rd ed.New York：Springer－Verlag，2004.