孙宝京

（沈阳炮兵学院电子侦察系，辽宁沈阳 110867）

基于正交多项式拟合的气象数据处理方法＊

孙宝京

（沈阳炮兵学院电子侦察系，辽宁沈阳 110867）

针对高空气象探测数据变化规律复杂、突变情况不可预测、数据量大等特点，提出了基于离散数据正交多项式最小二乘的分段拟合方法.首先，从计算稳定性角度，说明了采用离散数据的正交多项式最小二乘法的原因；其次，从曲线拟合的保形性角度，详细阐述了二次分段拟合原则；最后，以具有典型特征的气温探测数据为例，证明了采用基于离散数据正交多项式最小二乘的分段拟合方法能够获得明显优于传统内插方法的拟合精度，提高高空气象探测数据处理的精度和自动化处理程度.

离散数据；正交多项式；最小二乘；分段拟合；气象探测

当前气象探测站整理高空气象探测数据时，主要采用的方法是将整个探测空间分层，计算规定高度的中间数值，作为计算层数据，其他数据则采用依托计算层数据内插的方法计算.上述计算方法使用高度上的数据均由计算层数据插值得到，存在一定的截断误差和舍入误差；另外在较少的计算层数据中，必然会丢弃绝大多数探测数据，造成探测资源的极大浪费.随着气象探测及作业装备自动化水平和数据处理能力的不断提高，对高空气象探测数据处理精度和时效性提出了更高的要求，这也使得从根本上改变气象参数的计算方法成为可能［1］.

由于气象要素随时间、空间在不断地变化，而且探测仪器本身也受到许多复杂因素的影响，因此各种高空气象探测数据普遍具有数据量大、变化规律复杂、突变情况较多且不可预测等特点［2］.以弹道气象诸元中最重要的高空实时气温／高度曲线为例，当探测高度达到2万m时，采用电子探空仪探测的数据超过2 000组，虽然高空实时气温总体呈下降趋势，但是在局部经常出现不可预测的无规则变化.

针对高空气象探测数据特点，笔者基于离散数据正交多项式最小二乘拟合思想，提出根据数据变化率的变化情况，分段拟合各种高空气象探测数据曲线的方法.借助编程软件的自动处理，经过多次试验证明，此方法可直接得出气象通报所需要的气（虚）温－高度、气压－高度、风速－高度和风向－高度函数方程（高度为自变量），并且对高空气象探测数据处理的精确性、实效性和计算简捷性都有了很大的提高.因为高空实时气温／高度曲线在弹道气象诸元中最为重要，所以笔者将以此作为说明实例.

1 离散数据分段最小二乘拟合方法

用插值方法所找出的近似曲线，通过所有己知点，但是由观测或实验所获得的数据，不可避免地含有误差，这就使插值所找出的近似曲线保存所有观测误差，导致所得结果可能偏离了实际情况，出现曲线拟合的过度现象.而根据实际标准尽可能地通过节点的函数值近旁，以部分地抵消原始数据所包含的观测误差，则更具有实用价值，最小二乘拟合就是其中的一个重要方法［3］.

1.1 离散数据的正交多项式最小二乘拟合

在线性空间由Φ＝span（φ0，φ1，...，φn）求解最小二乘曲线拟合问题，经常会出现法方程组是病态方程组的情况，特别是当样本组数n偏大时更是如此，同时在求解法方程组时系数矩阵或右端项微小的扰动都可能导致解函数有很大的误差.为了确保计算过程的稳定性和精确性，笔者利用基于高空气象探测数据的正交多项式作为拟合函数系，使法方程组的系数矩阵变为对角矩阵，从而解得正交多项式的系数［4－5］.

根据点集｛x1，x2，...，xm｝，构造出相应的正交多项式系｛p0（x），p1（x），...，pn（x）｝.

由正交多项式三项递推关系，最高次项系数为1的正交多项式系｛pk（x）｝（k＝0，1，2，...，n）有如下递推关系：

其中pk（x）为最高项系数为1的k次多项式.由｛pk（x）｝正交性可知，

1.2 二次分段拟合原则

因一次完整综合气象探测的数据量大，若对整组数据进行一次性拟合，则拟合精度和计算效果都比较差.同时，为克服传统分段曲线拟合方法中对数据点分段时经验成分较多的缺点，笔者根据数据曲线斜率的变化情况对曲线进行分段拟合，并且加入了使相邻曲线连续，即曲线边界点必须连续的约束条件［6－7］.

考虑到高度是单调递增，为了适应高空气象数据曲线在局部随高度变化的无规则性，采取二次分段原则.

一次分段：在气温和高度曲线中，设Δti＝（ti＋1－ti）／（hi＋1－hi），其中ti和hi分别为探测数据中第i个探测点的气温和高度，ti＋1和hi＋1分别为探测数据中第i＋1个探测点的气温和高度.若Δti－1为负，Δti，Δti＋1，Δti＋2，...，Δti＋a（a≥1）为正，Δti＋a＋1，...，Δti＋a＋b（b≥1）为负，Δti＋a＋b＋1为正，则｛ti，...，ti＋a＋b｝为第i个分段，第i＋1个分段从点ti＋a＋b开始.

二次分段：在气温和高度曲线中，第i个分段已经由一次分段确定，设δi＋c＝Δti＋c－Δti＋c－1（1≤c≤a＋b－1）.若δi＋1，δi＋2，...，δi＋d（d≥1）均大于标准值δ0（为负数），δi＋d＋1≤δ0，且δi＋d＋2，...，δi＋d＋e（e≥1）小于或等于（－δ0），δi＋d＋e＋1＞（－δ0），则ti＋d＋e＋1为分段点，即｛ti，...，ti＋d＋e＋1｝为一个分段，下一个分段以ti＋d＋e＋1为起点，从δi＋d＋e＋2开始判断；若δi＋1≤δ0，且δi＋2，...，δi＋e（e≥1）小于或等于（－δ0），δi＋e＋1＞（－δ0），则ti＋e＋1为分段点，即｛ti，...，ti＋e＋1｝为一个分段，下一个分段以ti＋e＋1为起点，从δi＋e＋2开始判断［8－9］.

为使在单个分段内拟合曲线在误差允许范围内最大程度地保持数据曲线的形状，并且减少数据处理程序的计算量，实际计算过程对原始探测数据中心化计算后，采用如下做法进行拟合：

若a＋b≥5，则用四阶正交多项式为拟合函数系，即当一个分段包含4个以上的点时用四阶正交多项式拟合，

若a＋b＝4，则用三阶正交多项式为拟合函数系，即当一个分段包含4个点时用三阶正交多项式拟合，

若a＋b＝3，则用二阶正交多项式为拟合函数系，即当一个分段包含3个点时用二阶正交多项式拟合，

同时，使参与第i个分段拟合的第i个分段中的最后一个数据点，作为第i＋1个分段的第1个数据点参与第i＋1个分段的拟合，这样第i个分段的拟合函数和第i＋1个分段的拟合函数在分界点上的值相等，从而实现所有分段拟合函数在整体上保持连续［10］，即

2 计算实例

以编号为087233的GZZ8型电子探空仪探测数据为例.

图1是该组探测数据曲线中一部分，温度t∈［－61.31，－62.27］，高度H∈［15 125.89，1 5 494.56］.根据文中的分段规则，数据处理系统自动将此段数据曲线分为5段进行拟合.

图1 温度和高度探测数据分布

第1个分段为前13个点，h∈［15 125.89，15 230.23］，拟合函数为

平方误差为0.08.

第2个分段为后续7个点，h∈［15 230.23，15 289.47］，拟合函数为

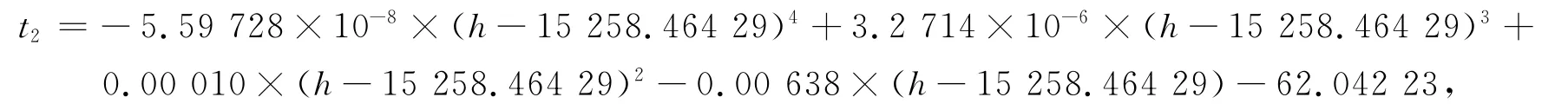
平方误差为0.03.

第3个分段为后续10个点，h∈［15 289.47，15 397.85］，拟合函数为

平方误差为0.02.

第4个分段为后续5个点，h∈［15 397.85，15 439.32］，拟合函数为

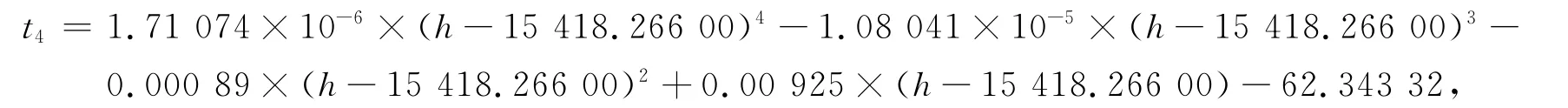
平方误差为0.01.

第5个分段为最后7个点，h∈［15 439.32，15 494.56］，拟合函数为

平方误差为0.03.

根据传统高空气象探测数据处理方法，14 000～16 000m高度范围内的相关气象数据从标准高度层14 000m和16 000m处的实际探测数据进行线性内插得到.在此例中，14 000m和16 000m处的气温分别为－56.16℃和－62.37℃，从而内插得到高度为15 142.00，15 276.4，15 378.67，15 417.06，1 5 479.1m处的气温.各高度对应的实际探测值、内插结果和拟合结果见表1.由表1可见，采用基于离散数据正交多项式最小二乘的分段拟合法，可以获得比传统内插法更好的拟合精度.

表1 不同高度实际探测值、内插值、拟合值对应关系

3 结语

针对高空气象探测数据量大、变化规律复杂、突变情况较多且不可预测等特点，提出了基于离散数据正交多项式最小二乘的分段拟合法.经过实践证明，该方法能够根据算法自动分段，拟合出符合精度要求的曲线，在处理程序自动计算过程中确保计算的稳定性和高效性，避免传统高空气象探测数据处理方法中不断累计的舍入误差对结果的影响，提高高空气象探测数据处理结果的精度和自动化处理程度.

［1］ 孙宝京.炮兵防空兵气象信息系统研究［D］.沈阳：东北大学，2004.

［2］ 曲延禄.外弹道气象学概论［M］.北京：气象出版社，1987：59－176.

［3］ FRANK R.Scattered Data Interpolation：Tests of Some Methods［J］.Mathematical Computation，1982，38：181－200.

［4］ MICCHELLI C.Interpolation of Scattered Data：Distance Matrix and Conditionally Positive Definite Functions［J］.Constructive Approximation，1986，2：11－22.

［5］ 蔺小林，蒋耀林.现代数值分析［M］.北京：国防工业出版社，2004：212－255.

［6］ WU Zong-min，SCHABACK R.Shape Preserving Properties and Convergence of Univariate Multi-Quadric Quasti-Interpolation［J］.ACTA Mathematice Application Sinica，1994，10：441－446.

［7］ GREGORY J A.Shape Preserving Spline Interpolation［J］.Computer-Aided Design，1986，18（1）：53－57.

［8］ KAUFMANN E，KLASS R.Smoothing Surfaces Using Reflection Lines for Families of Splines［J］.Computer-Aided Design，1988，20（6）：312－316.

［9］ HOSCHEK J.Smoothing Curves and Surfaces［J］.Computer-Aided Geometric Design，1985，2（1－3）：97－105.

［10］ JORG PRTERS.Local Smooth Surface Interpolation：A Classification［J］.Computer-Aided Geometric Design，1 990（7）：191－195.

（责任编辑 向阳洁）

Piecewise Curve Fitting Method of Processing Meteorological Data Based on the Orthogonal Polynomial

SUN Bao-jing

（Department of Electronic Reconnaissance，Shenyang Artillery Academy，Shenyang 110867，China）

In accordance with the characterics of the large number and complex and unpredicted trend on change of the meteorological detecting data，the piecewise curve fitting method based on the least squares of orthogonal polynomial for scattered data is presented.Firstly，the reason of using the least squares of orthogonal polynomial for scattered data is introduced from the respect of the stability of data processing.Secondly，the principle of twice piecewise curve fitting is set out in detail from the respect of the shape preserving feature of curve fitting.Finally，as the temperature detecting data for example，it is proved clearly that the twice piecewise curve fitting method can make much better fitting precision than the traditional interpolation method，and improve the level of precision and automation of the meteorological detecting data processing.

scattered data；orthogonal polynomial；least squares；piecewise curve fitting；meteorological detecting

P412.2；TP274

A

10.3969／j.issn.1007－2985.2013.05.012

1007－2985（2013）05－0049－04

2013－01－24

孙宝京（1968－），男，山东五莲人，沈阳炮兵学院教授，主要从事弹道气象学研究.