吴建强 侴万禧

（1.安徽理工大学 理学院，安徽 淮南 232001；2.安徽理工大学 土木建筑学院，安徽 淮南 232001）

0 引言

在各种各样的图中，有一类简单的，但却是重要的图，就是所谓的“树”。它是基尔霍夫在解决电路理论中求解联立方程问题时首先提出来的，可惜他的发现超越了时代而长期没有引起重视。树与图中其他一些基本概念，如回路、割集等有密切的联系，是图论中比较活跃的领域。在图论中，解决一些悬而未决的问题往往首先从树这类图入手。许多问题对一般的图未能解决或者没有简便的方法，而对于树，则已完满解决，且方法较为简便。

给定一个无向图G，若G的一个生成子图T是树，则称T为G的生成树。图的生成树不是唯一的。但任何连通图至少有一颗生成树。所有生成树中具有最小数的生成树称为最小生成树，求最小生成树是实际问题的需要，例如“为了把若干城市连接起来，设计最短通信线路”，“为了解决若干居民点供水，要求设计最短的自来水管线路”等等。

1 基本思路

定义1 设G（p,q）为p个顶和q个边的任意连通图，则G（p,q）中任意p-1个边所导出的S（G）个子图称为生成子图。

定义2 设图G(p,q)中存在S(G)个生成子图，则S（G）个生成子图中T（G）个不含圈的生成子图称为生成树，C（G）个含圈的生成子图称为含圈的生成子图，并有 S（G）=C（G）+T（G）。

定理1 设G（p,q）为任意连通图，则G（p,q）中任意p-1个边所导出的生成子图的个数为

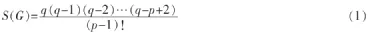
S（G）个生成子图中含圈的生成子图的个数为

S（G）个生成子图中不含圈的生成树的个数为

式中：Ci（G）—图 G（p,q）中 Ci的个数；个边中任取p-j个边的选择数。

证明：不失一般性，设 G（p,q）为 p＝4，q＝6 的完全图 K4，且 K4中 C3的个数 C3（G）＝4；C4的个数 C4（G）＝1，若定理 1 为真，则 K4中 P—1=3个边所导出的生成子图的个数

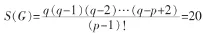
S（G）＝20个生成子图中含圈的生成子图仅与圈C3有关系，故含圈的生成子图的个数为

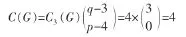
S（G）＝20个生成子图中不含圈的生成树的个数为

定理1得证。

定理2设G（p,q）为任意连通图，则G（p,q）中p-1个边所导出的S(G)个生成子图的构造归结为

b＝S（G），v＝p，r＝A，k＝p－1，λ＝B 的（b，v，r，k，λ）设计中 S(G)个区组的构造。由于G（p,q）中q个边的编号为区组的变元，S(G)个生成子图与S(G)个区组一一对应，C（G）个含圈的生成子图与C（G）个区组一一对应，T（G）个生成树与 T（G）个区组一一对应，且有 S（G）＝C（G）＋T（G）

证明：不失一般性，设则 G（p,q）为 p＝4，q＝6 的完全图 K4，若定理2 为真，则完全图 K4的个生成子图的构造归结为 b＝20，v＝p＝4，r＝6，k＝p－1＝3，λ＝4 的（b，v，r，k，λ）设计中下列 0个区组 ：（1，2，3），（1，2，4），（1，2，5），（1，2，6），（1，3，4），（1，3，5），（1，3，6），（1，4，5），（1，4，6），（1，5，6），（2，3，4），（2，3，5），（2，3，6），（2，4，5），（2，4，6），（2，5，6），（3，4，5）,(3,4,6),(3,5,6),(4,5,6)的构造，当K4中q=6个边的编号被确定后，S(G)=20个生成子图与20个区组一一对应，20个生成子图中有4个含圈的生成子图，有16个不含圈的生成树。 亦即：T（G）＝16，C（G）＝4 且

S（G）＝C（G）＋T（G），见图 1。 定理 2 得证。

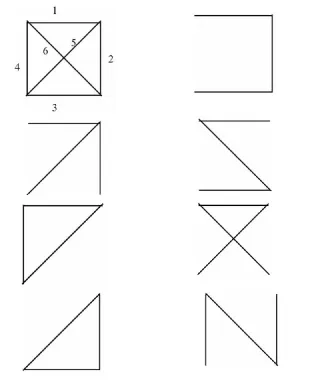
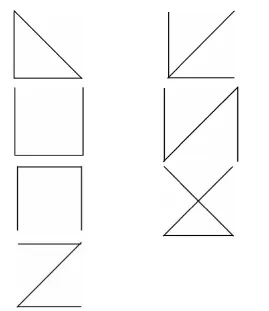
图1

2 八面体平面的生成子图

1）生成树的个数

设图 G（p,q）为 p＝6，q＝12 的八面体平面图，图 G（6，12）中的 C3的个数 C3（G）＝8，C4的个数 C4（G）＝15，C5的个数 C5（G）＝24，则据定理 1，图 G（6，12）中生成子图的个数为

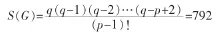
S（G）＝792个生成子图中含圈的生成子图的个数C（G）＝393

S（G）＝792个生成子图中不含圈的生成树的个数为：

2）S（G）个生成子图的构造

G（6，12）中 S（G）＝792 个生成子图可借助于 b＝792，r＝330， k＝5，λ＝120 的下列区组的（b，v，r，k，λ）设计 ：（1，2，3，4，5）（1，2，3，4，6），（1，2，3，4，7），（1，2，3，4，8），（1，2，3，4，9），（1，2，3，4，10），（1，2，3，4，11），（1，2，3，4，12），（1，2，3，5，6），（1，2，3，5，7）…(8,9,10,11,12)。 当图 G（6，12）中q＝12个边的编号被确定后，792个区组中的399个区组与399个生成树一一对应，792个区组中的393个区组与393个含圈的生成子图一一对应，且有 S（G）＝C（G）＋T（G）的关系。 这说明：生成树的个数的结算结果与实际构造想吻合。

3 结束语

由于Cayley公式仅适用于任意完全图Kp中生成树个数的计算。而任意非完全图中的生成树的计算问题，可以运用本文方法来解决，尽管计算繁琐，但却解决了任意图生成树的构造。任意平面中的生成树在遥控技术等领域有着广泛的应用，根据本文的思想，一种基于森林分解的生成树的构造和计数方法将能够得到，也必将得到广泛的运用。

［1］Bollobasb.Graph Theory[M].New York：San Francisco,Academic Press,1978.

［2］Freds.Roberts BarryTesman.Applied Combinatorics[M].beijing：China Machine Press,2007.

［3］侴万禧.完全图的生成树的构造与计算[J].山东师范大学学报：自然科学版,2007,11(4)：72-72.

［4］侴万禧.任意的生成树的构造与计数[J].山东师范大学学报：自然科学版,2008,23(1)：14-15.

［5］侴万禧,郝朋伟.完全二分图的生成树的个数[J].阜阳师范学院学报,2008,25(4)：12-14.

［6］侴万禧,等.平面的四着色与对偶图的H圈[J].沈阳师范大学学报：自然科学版,2009,27(3)：264-266.

［7］徐俊明.图论及其应用[M].中国科学技术大学出版社,2004.

［8］侴万禧.2t名运动员的循环赛和对集的划分[J].安徽理工大学学报：自然科学版,2006,26(1)：64-69.

［9］侴万禧.边矩阵K2n+1的k+1-边着色与循环赛的安排[J].安徽建筑工业学院学报：自然科学版,2006,14(4)：1-5.

［10］侴万禧,林雨.12 面体中的 H 圈[J].扬州大学学报：自然科学版,2007,10(4)：32-38.