李 砚，杜 纲，刘 波,2b

0 引言

鲁棒优化是一种处理不确定参数优化问题的重要方法，由Soyster[1]于1973年首次提出，其区别于其它不确定优化方法的重要特征是模型对数据的不确定具有免疫性。由于鲁棒优化对于不确定参数没有假定分布，鲁棒解被定为最坏不确定情景下使目标函数具有最优值的解。因此，鲁棒优化规避了估计风险，同时也规避了低概率事件发生所带来的巨大风险。鲁棒优化的核心思想是将不确定性问题以一定的近似程度转化为多项式时间内可以解决的确定性凸优化问题。

双层规划是具有主从递阶结构的层次优化问题，它将一个参数化的优化问题作为其约束条件[2]。在其层次决策框架中，下层决策者在上层决策者给定参数条件下优化自己的目标函数，而上层决策者基于下层决策者可能的最优反应来确定自己的决策参数以优化自己的目标函数，决策过程中上下层的决策与选择行为相互依存。目前，双层规划模型在委托代理、供应链等诸多领域已经有着非常广泛的应用。

本文将提出鲁棒双层规划模型，针对目标函数和约束条件的系数均在椭球不确定集内扰动的情形，通过不等式约束处理将鲁棒双层规划模型转化为下层含有二阶锥约束的非线性确定性问题进行求解，以此获得鲁棒解。对于含有二阶锥约束(决策变量线性函数的二范数小于等于决策变量的线性函数)的规划称为二阶锥规划，它是对称锥的特例，属于非光滑凸规划[3]。关于二阶锥规划的求解，具有代表性的算法主要有内点法、光滑牛顿算法、非内部连续化算法等。而双层规划的求解，即使是线性的，也是NP-hard的[4]。目前，双层规划的求解方法主要分为两类：精确算法和智能算法。精确算法大多依赖于解空间的特性，无法解决一般的非线性规划问题；智能算法具有较优的全局搜索能力，对目标函数要求较低，逐渐被用来解决双层规划问题。因此，本文拟提出一种混合遗传算法求解鲁棒双层规划模型转化后的这类下层含有二阶锥约束的确定性双层规划。

1 鲁棒双层规划模型

1.1 问题描述

基于不确定双层规划中上下两层的决策者均需获得鲁棒解的前提假设，考虑向量形式所表示的双层规划：

其中y解自于下面规划问题：

其中，x∈Rm×1,y∈Rn×1,ci∈Rm×1,di∈Rn×1(i=1,2),A ∈ Rk×m,B ∈ Rk×n,h∈Rk×1。

假设式(1)的目标函数及约束条件的系数(c1,d1,c2,d2,A,B,h)均在椭球集合μ内扰动，记

其中，c∗1,d1∗,c2∗,d2∗,A∗,B∗,h∗为给定的数据，A和A∗的第i个行向量为aTi和(ai∗)T，B和B∗的第i个行向量为bTi和(bi∗)T， 设 P01， P02∈ R(m+n)×(m+n), Pi∈R(m+n+1)×(m+n)为给定的尺度变换。

1.2 模型的转化

系数在椭球集合μ内扰动的鲁棒双层规划可以通过如下推导转化成为系数确定的双层规划。

1.2.1 上层规划问题的转化

首先讨论式(1)中上层规划问题，其系数在椭球集合μ内扰动时，如何转化为确定性问题。根据双层规划的库恩—塔克条件法以及式(2)所表示的等价形式[5]

可得：

其中，Θ(d)={( x ,y,u,v)|Ax+by≥h,d2=BTu+v

当式(3)中的系数c1,d1∈μ时，利用文献[5]中转化形式：

其中c∗是给定数据，P0是相应的尺度变换。

可以将不确定约束条件c1Tx+d1Ty≤t转化为确定的约束条件

那么再次利用式(2)，得到

显然，式(5)是式(6)用K-T条件法表示的等价形式:

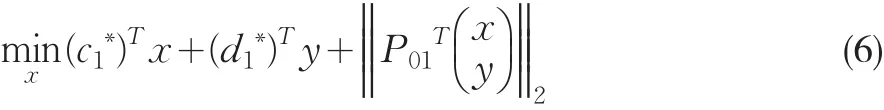
其中y解自于下面规划问题：

从而就把系数不确定的上层规划转化为确定性规划。

1.2.2 下层规划问题的转化

根据双层规划的决策框架以及上下两层决策者均需获得鲁棒解的前提假设，一旦上层规划给定决策变量x，那么下层规划就是一个单层的鲁棒规划问题。同理，利用式(2)所表示的等价形式将下层目标函数转化成约束条件，再通过式(4)的转化形式对约束条件进行推导，则系数不确定的下层问题转化为确定性问题。综上，鲁棒双层规划模型得以转化为式(7)所表示的具有确定系数的双层规划问题：

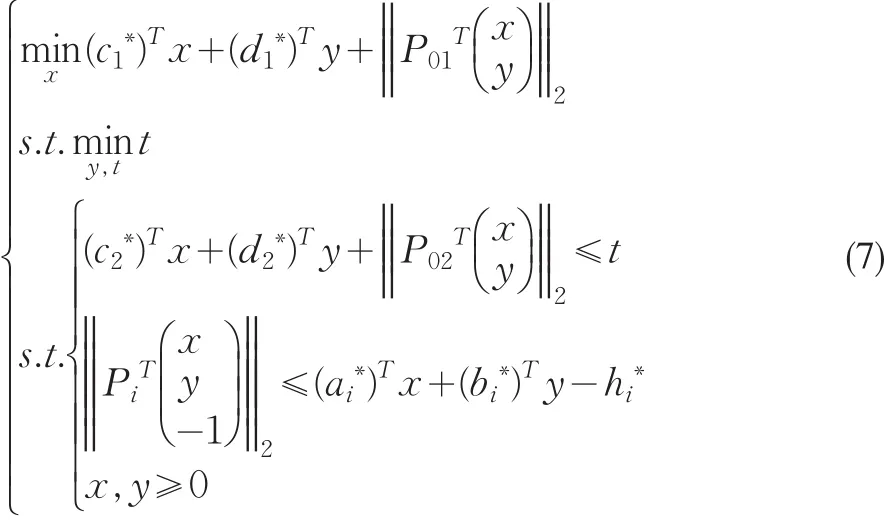
式(7)是下层含有二阶锥约束的双层规划。

2 混合遗传算法

上述鲁棒双层规划模型，经过模型转化得到了下层含有二阶锥约束的确定性双层规划。本文提出一种混合遗传算法求解这类转化后的非线性双层规划问题。混合遗传算法求解该问题的核心思想是：首先给出上层种群中个体x，通过改进的非内部连续化算法[6，7]求解下层的二阶锥规划,得到上层种群中每个个体x所对应的下层最优解y，进而由上层目标函数计算个体的适应度；然后对该群体进行选择、交叉、变异等遗传运算,通过上下层的反复迭代，逐渐逼近最优解。

2.1 非内部连续化算法

对下层二阶锥规划的求解，本文采用基于单个牛顿方程的非内部连续化算法[6]。非内部连续化方法的主要思想是：利用一个光滑函数把问题重新表述成一个参数化的光滑方程组，每步迭代利用牛顿法进行求解，通过令参数趋于零，期望得到原问题的一个解。该算法可以起始于任一点且不要求光滑路径和迭代点位于正区域。文献[6]提出了一个改进的求解对称锥互补问题的非内部连续化算法。改进后算法的突出特点是在每步迭代中至多需要解一个线性方程组，并且在弱的条件下具有全局线性收敛性和局部二次收敛性，该算法被用来求解二阶锥规划。其中采用的二阶锥光滑函数ϕμ为φμ(x,s):=φ(μ,x,s)=x+s-，其中μ∈R给定。

2.2 编码和适应度函数设计

本文在遗传算法中采用格雷码对个体进行编码，每个个体被遗传到下一代种群中的概率是由该个体的适应度来确定的。在这里使用指数尺度变换的适应度分配方法。指数尺度变换时，新的适应度是原适应度的某个指数。指数尺度变换的公式为：

其中，系数β决定了选择的强制性，β越小，原有适应度较高的个体的新适应度就与其他个体的新适应度相差较大，即增加了选择个体的强制性。

2.3 操作算子策略

2.3.1 选择算子

选择算子采用两种策略：一种是精华直接复制策略；还有一种是随机遍历抽样策略。精华直接复制策略按适应度排列群体中的个体，采取最优保存策略复制适应度值最大的个体并使它直接进入下一代；而随机遍历抽样策略将下一代个体中其余个体采用随机遍历抽样方法产生，即：使用N个相等距离的指针，N是要求选择的个数。种群被随机排列在[ ]0,Sum/N范围内产生一随机数作为指针p tr，N个个体由相隔一个距离的N个指针[p tr,p tr+1,p tr+2,…,p tr+N-1]选择，选取适应度范围在指针位置的个体。另外，个体完全按它们在种群中的地位选择，因此获得最小的个体扩展和零偏差[8]。

2.3.2 交叉和变异算子

采用多点交叉策略。多点交叉有m个交叉位(当m=1时为单点交叉),ki∈{ }1,2,…,l-1是交叉点，l是染色体的长度，m个交叉位是通过随机数选择的，没有重复、按升序排列。父母染色体中在两个相连的交叉位间的基因进行交换，产生两个新的子代。

设Pm为变异概率，产生一个[0,1]区间的随机数r，如果r≤Pm，则对个体编码串中以变异概率随机指定某一位或某几位基因位上的值做反转变异运算(即0→1或1→0)或用其他等位基因值来代替，从而产生出新一代的个体。

2.4 算法过程

根据转化后模型特点，结合上述讨论，给出一种混合遗传算法，整个算法的流程如图1所示，具体步骤如下：

图1 算法的流程图

(1)随机产生初始种群X,确定种群规模N以及交叉率Pc和变异率Pm,同时设定最大迭代数MAXGEN(终止条件)。

(2)对于上层初始种群X中的每个个体xi(i∈[1,N])代入下层二阶锥规划，利用改进的非内部连续化算法[6]求得上层种群X的每个个体xi所对应的下层规划的最优解yi，上层目标函数作为适应度函数，再把X和Y代入到适应度函数，得到相应的适应度值。

(3)选择算子操作，根据适应度函数值的大小对种群X的个体进行选择,重复进行该过程,完成个体选择过程。

(4)应用遗传操作算子对选入下一代的个体进行交叉和变异算子操作，产生新的个体进入下一代。

(5)终止条件判断(迭代次数大于最大迭代数)。如果条件满足,则进化终止；否则,转步骤(2)。

(6)输出模型的最优解，算法运行结束。

3 数值算例

考虑如下鲁棒双层规划问题：

其中y解自于下面规划问题:

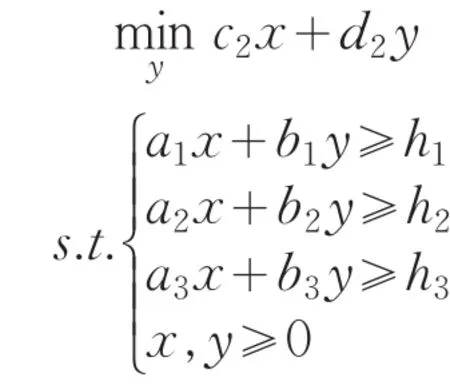
其中cl,dl(l=1,2);ai,bi,hi(i=1,2,3)

均属于椭球扰动集μ，表示如下：

给定数据如下：

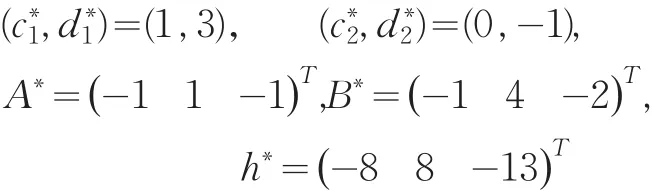
在区间[0,0.3]内随机产生的尺度变换值如下：

利用2.2节中模型的转化方法，并令z=(x y)T,得

其中y解自于下面规划问题：

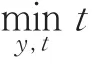
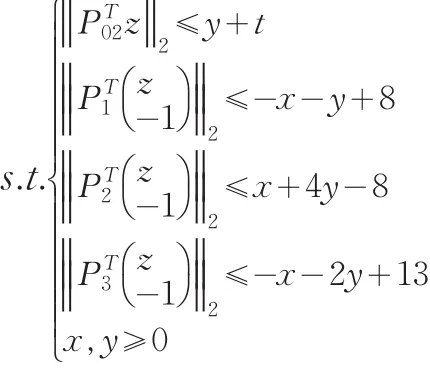
由上述算法步骤，通过MATLAB编程实现得到上层决策变量的鲁棒解为:x=6;上层目标函数的最优值为:Fmin=12.7294;下层决策变量的鲁棒解为：y=1.6139;下层目标函数的最优值为：fmin=0.4918.

当假设所有尺度变化均为零，即参数处于名义值时，问题本身为确定的线性双层问题，即文献[2]的算例。利用该算法得到上层决策变量的最优解为:x=6;上层目标函数的最优值为:Fmin=12;下层决策变量的最优解为:x=2;下层目标函数的最优值为:fmin=-2。与算例同解。

4 结语

本文基于上下两层决策者均需获得鲁棒解的前提假设提出了系数不确定双层规划的鲁棒问题，采用不等式约束处理将原问题转换为下层是二阶锥规划的确定性双层规划问题。根据转化后模型特点，设计了相应的混合遗传算法，并且由于常值函数、线性函数、欧氏范数、P范数函数及偶幂函数都具有二阶锥集性质，可以将含有这些函数的规划转化为二阶锥规划进行求解[5]。因此，该算法不仅能获得高质量的全局最优解，而且本身具有通用性，可以求解更一般的双层规划问题。本文通过算例验证了算法的有效性及可行性。

[1]Soyster A L.Convex Programming with Set-inclusive Constraints and Applications to Inexact Linear Programming[J].Operations Research,1973,(21).

[2]Dempe S.Foundations of Bilevel Programming[M].Boston:Kluwer Academic Publisher,2002.

[3]Alizadeh F,Goldfarb D.Second-order Cone Programming[J].Mathe⁃matical Programming,2003,95(1).

[4]Jeroslow R.The Polynomial Hierarchy and a Simple Model for Com⁃petitive Analysis[J].Mathematical Programming,1985,32.

[5]Lobo M S,Vandenberghe L,Boyd S,etc.Applications of Second-order Cone Programming[J].Linear Algebraand its Applications,1998,284(1).

[6]Lu N,Huang Z H.Convergence of a Non-interior Continuation Algo⁃rithmfor the Monotone SCCP[J].Acta Math.Appl.Sinica(English Se⁃ries),2010,(4).

[7]Huang Z H.The Global Linear and Local Quadratic Convergence of a Non-interior Continuation Algorithm for the LCP[J].IMA Journal of Numerical Analysis,2005,(25).

[8]雷英杰,张善文,李续武等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.