介于经典型和乘积型的奇异积分算子*
2012-05-10谭超强
谭超强
(汕头大学理学院数学系,广东 汕头 515063)
由于偏微分方程和复分析等领域的研究发展,产生了一系列具有奇性的积分算子,人们需要对这些算子的性质进行探索和研究。于是在这种背景的激励下,Calderon和Zygmund等人经过多年的研究,建立出一套比较完善的单参数奇异积分算子理论[1-4],如今它已经成为调和分析领域的核心内容。这类型算子的特点是核函数满足大小条件、光滑性条件与消失矩条件,而这类算子的最重要性质之一就是Lp有界性(1 然而随着多复变函数等领域的发展,人们发现有些算子与Calderon-Zygmund奇异积分算子很类似,但是却不满足单参数Calderon-Zygmund奇异积分算子的条件。为解决这些问题,E.M.Stein和R.Fefferman等人引入一套多参数乘积型的奇异积分算子理论[5-7],很好地解决了这些问题。这套多参数理论的特点是把单参数理论中的核函数大小条件与光滑性条件同时降低,但是却加强了消失矩条件,依然能保证这类算子的Lp有界性 (1 这两套理论有着本质的区别,但同时有着诸多的联系。在这两套算子理论的基础上,本文将建立另外一套介于单参数与多参数间的奇异积分算子理论,给出其Lp有界性。我们给出的这类算子特点是核函数比单参数的奇异积分算子的大小条件和光滑性条件要求低,但是保持消失矩条件不变。因此经典的单参数奇异积分算子就是我们这套理论的特殊情形,同时在形式上与乘积型的算子非常类似。 1.1.1 经典的单参数奇异积分算子理论 假设存在常数C,使得核K(x):Rn→R满足: 注1 单参数核的一个重要性质是单参数展缩不变,即对任意的t>0,tnK(tx)一致地满足上面大小条件、光滑性条件和消失矩条件。 1.1.2 多参数奇异积分理论 假设存在常数C,使得核K(x,y):Rm×Rn→R满足: 注2 多参数核的一个重要性质是多参数展缩不变,即对任意的t,s>0,tmsnK(tx,sy)一致地满足上面大小条件、光滑性条件和消失矩条件。 我们知道单参数理论与多参数理论虽然方法上很多相同之处,但是却有着本质的不同。为研究这两种理论之间的联系,本文将建立一套介于经典单参数与多参数乘积型的奇异积分算子理论。该理论某种程度上可看作为连结这两套理论的纽带,对它的研究将丰富了奇异积分算子理论体系,有助于我们加深对奇异积分算子的理解与认识。为了更加清楚表述我们的理论,我们只考虑R2上这种简单的情形。下面是本文的主要定理。 定理1 给定0<δ<1,假设存在常数C,使得核K(x):R×R→R满足: 注3 (i) 我们指出经典的单参数奇异积分算子包含在我们的类里面,同时形式上与多参数的乘积型奇异积分算子理论类似。 (iv) 该类算子是单参数展缩不变的,即对任意的t>0,t2K(tx,ty)一致地满足上面大小条件、光滑性条件和消失矩条件。 注意到 ξ,x2)e-2πi(x1ξ1+x2ξ2)dx1dx2+ I+II+III+IV 对于项I,利用核K的大小条件和消失矩条件,有 (|x1ξ1|+|x2ξ2|)dx1dx2+C≤C. 对于项II,对变量x2进行分部积分,有 |II|≤ II1+II2 假定f是紧支集光滑函数,那么 I+II 对于项I,利用核K的条件,有 |I|≤F(x)· 其中F(x)为紧支集特征函数。 对于项II,我们对积分项用绝对值估计,有 而该函数属于Lp(R2)。 利用控制收敛定理,我们就得到需要的结论。 众所周知,g(f)与函数f是Lp(R2)互相控制的,即存在常数C1,C2,使得 C1‖f‖p≤‖g(f)‖p≤C2‖f‖p 为证明算子T的Lp(R2)有界性,首先我们需要证明下面的引理: 证明 分三种情况讨论:(a) |x1|≥2,|x2|≥2; (b) |x1|≥2,|x2|<2或者|x1|<2,|x2|≥2;(c) |x1|<2,|x2|<2。 对于情形(a): |x1|≥2和|x2|≥2,利用函数ψ的消失矩条件,有 |K*ψ(x)|= 对于情形(b):|x1|≥2,|x2|<2或者|x1|<2,|x2|≥2,我们有 |K*ψ(x)|= 对于情形(c): |x1|<2,|x2|<2,利用核K的消失矩条件,有 |K*ψ(x)|= ψ(x1,x2))dy1dy2|+ (|y1|+|y2|)dy1dy2|+C≤ 这样我们就完成了引理1的证明。 根据引理1得到的结论,我们又可以得到如下的引理: 引理2 假定0<λ≤min(δ,1-δ),j,j′∈Z, 那么有 引理2的证明是规范的,它需要利用下面两个事实: (a)卷积算子的交换性,即ψj*K*ψj'(x)=K*(ψj*ψj')(x); (b)ψj*ψj'(x)满足引理1证明中函数ψ(x)需要用到的条件。证明过程这里省略。 根据引理2得到的结论,对j,j′∈Z, 有 |ψj*K*ψj'*(ψj'*f)(x)|≤C2-|j-j'|Ms(ψj'*f)(x) 其中Msf(x)为R×R上的强极大函数。 ‖T(f)‖p≤C‖g(Tf)‖p= 对任意的紧支集光滑函数f(x)均成立。 最后利用紧支集光滑函数在Lp(R2)空间上是稠密的性质,我们就可以把算子T延拓为Lp(R2)上的有界线性算子,这样就完成了定理1的证明。 本文建立了一套介于单参数经典型与多参数乘积型间的奇异积分算子理论,证明其Lp有界性(1 参考文献: [3]STEIN E M.Note on singular integrals [J].Proc Amer Math Soc,1957,8: 250-254. [4]ZYGMUND A.On singular integrals [J].Rend Mate Appl,1957,16: 468-505. [5]FEFFERMAN R,STEIN E M.Singular integrals on product spaces [J].Adv Math,1982,45(2): 117-143. [6]JOURNE J L.Calderon-Zygmund operators on product spaces [J].Rev Mat Iberoamericana,1985,1: 55-92. [7]RICCI F,STEIN E M.Multiparameter singular integrals and maximal functions [J].Ann Inst Fourier (Grenoble),1992,42: 637-670. [8]STEIN E M.Harmonic analysis: real-variable methods,orthogonality and oscillatory integrals [M].Princeton: Princeton University Press,1993.1 定理的提出
1.1 单参数与多参数奇异积分算子理论简介
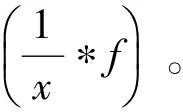
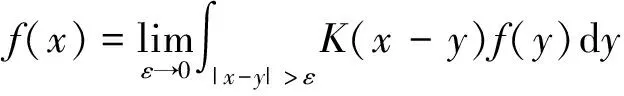
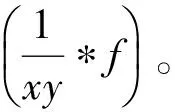
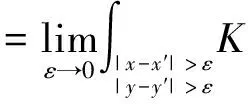
1.2 主要定理
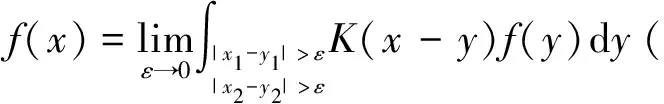
2 主要定理的证明
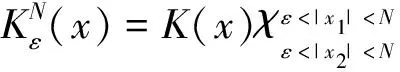
2.1 第一步 证明算子是L2(R2)上一致有界的
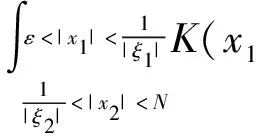
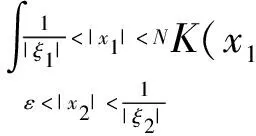
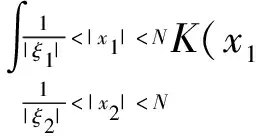
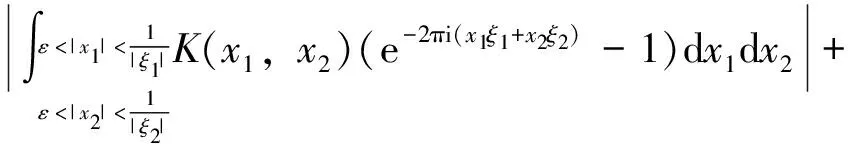
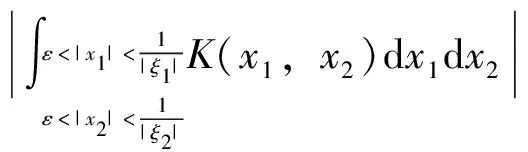
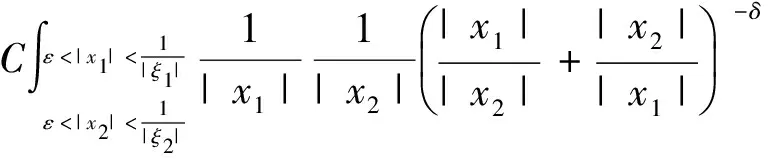
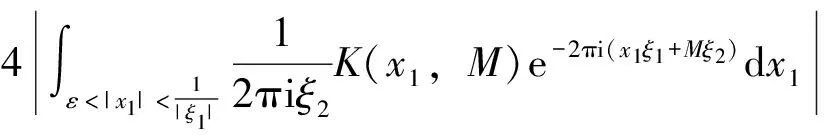

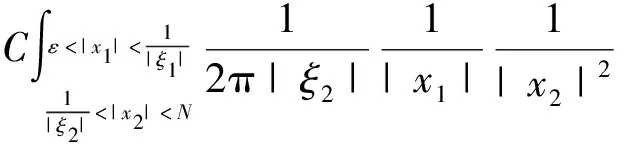
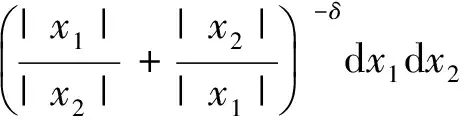
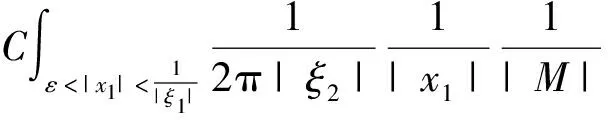

2.2 第二步,对紧支集光滑函数f,证明在Lp(R2)意义下收敛(1
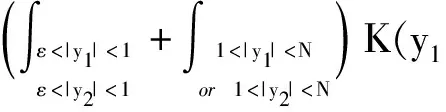
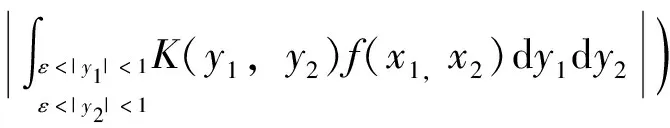
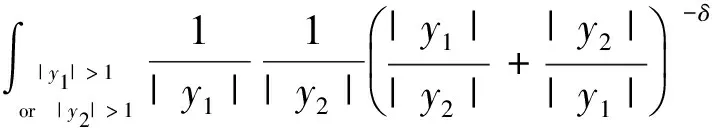
2.3 第三步,证明算子T是Lp(R2)有界的(1
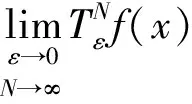
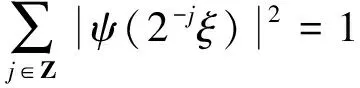
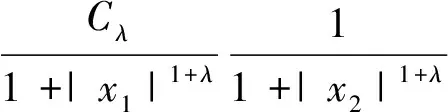
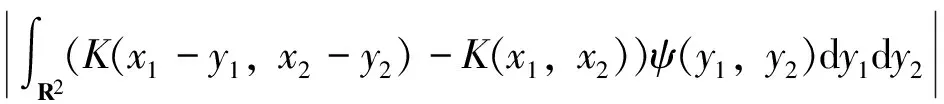
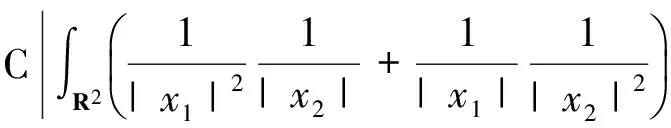
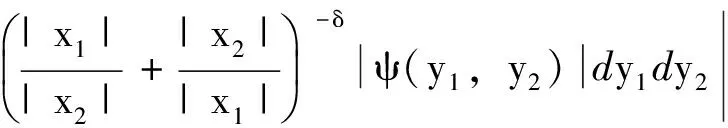
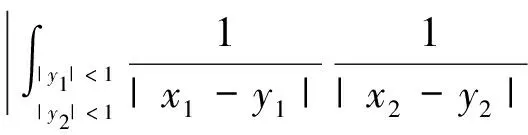
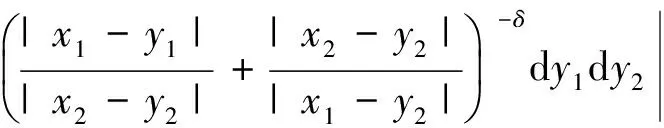
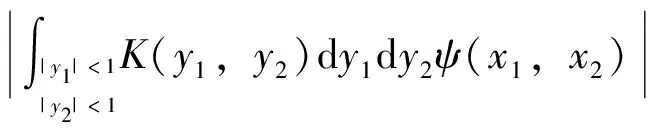
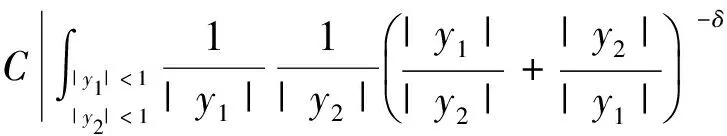
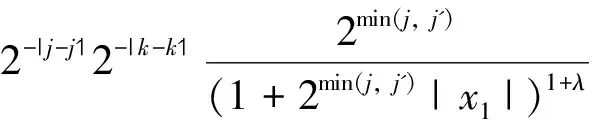
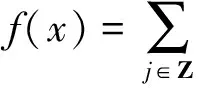
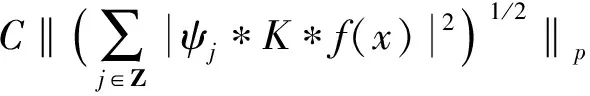
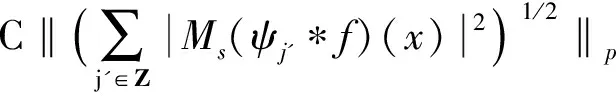
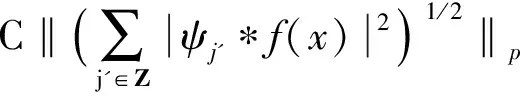
3 结 论
