杨利容，简兴祥

（1.成都理工大学，四川 成都 610059；2.四川省核工业地质局，四川 成都 610021）

0 引言

在大地电磁（MT）反演迭代过程中，需要实时生成多种图件提供给反演解释人员，以动态了解反演拟合的情况，如反演结果二维等值线图、反射系数二维等值线图、实测数据二维等值线图以及当前模型正演的拟合结果二维等值线图等。但由于数据采集技术、工区客观条件上的种种限制以及计算机的计算能力等原因，地球物理学中的大多数数据都是不规则的离散数据。绘制以上各种数据的等值线图时，首先需要对离散数据进行网格化处理，将稀疏的、不规则分布的数据插值加密为规则分布的数据，以适应成像绘图的需要。在MT反演迭代过程中对数据进行网格化处理必然对插值算法的可靠性和实时性要求比较高。网格化方法的好坏不仅直接影响到网格化数据的质量、精度和可信程度，而且还将进一步影响到数据解释处理图件的质量、效果和可靠性。为此有必要研究一种可靠性高、精度能满足要求、针对大数据量快速实时的二维网格化方法。

目前在地球物理领域普遍使用的网格化方法主要有最小曲率插值法（minimum curvature splines）、Kriging插值法、加权反距离插值法等［1］。各种方法各有优缺点。如最小曲率插值法速度快，适合处理数据量大的情况，由于其主要考虑曲面的光滑性，不能达到精确的插值结果，容易超出最大值和最小值的范围；Kriging插值法根据原数据所隐含的趋势特征，以区域化变量理论为基础，以变差函数为主要工具，在保证研究对象的估计值满足无偏性条件和最小方差条件的前提下求得估计值，是一种精度比较高的网格化插值算法，但该方法随着数据量的增大计算速度较慢［2］。所以上述常用的插值方法不能满足实时成像的要求。基于Delaunay三角剖分的快速插值算法由于采用所有的数据点去构造最佳Delaunay三角网，原始数据点在插值后保持不变，其他待插点只跟它所处的三角形的三个顶点相关，因而是一种局部插值方法；另一方面，该方法并不进行外插，因此适合于网格化处理带地形特征的数据。由于该方法能够很好的拟合地形，因此被广泛的应用到数字高程模拟（DEM）中，并出现了很多算法［11－13］。本文拟实现一种基于 Delaunay三角剖分的线性插值的算法，并将其应用到自主开发MT二维反演软件快速成像二维网格化处理中。

1 Delaunay三角剖分

如何把一个散点集合剖分成不规则的三角形网格（Triangular Irregular Network，TIN），这就是散点集的三角剖分问题。在所有生成TIN的方法中，Delaunay三角网最优，它尽可能避免了病态三角形的出现，常常被用来生成TIN。对于给定的初始点集P，有多种三角网剖分方式，而Delaunay三角网有以下特性：其Delaunay三角网是唯一的；三角网的外边界构成了点集P的凸多边形“外壳”；如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大，从这个意义上讲，Delaunay三角网是“最接近于规则化”的三角网。

要满足Delaunay三角剖分的定义，必须符合两个重要的准则：（1）空圆特性，任何一个Delaunay三角形的外接圆的内部不能包含其它任何点；（2）最大化最小角特性，每两个相邻的三角形构成的凸四边形的对角线，在相互交换后，六个内角的最小角不再增大。

理论上为了构造Delaunay三角网，Lawson提出局部优化过程LOP（Local Optimization Procedure），一般三角网经过LOP处理，即可确保成为Delaunay三角网。如图1所示，先求出包含新插入点p的外接圆的三角形，这种三角形称为影响三角形，删除影响三角形的公共边，将p与全部影响三角形的顶点连接，完成p点在原Delaunay三角形中的插入。

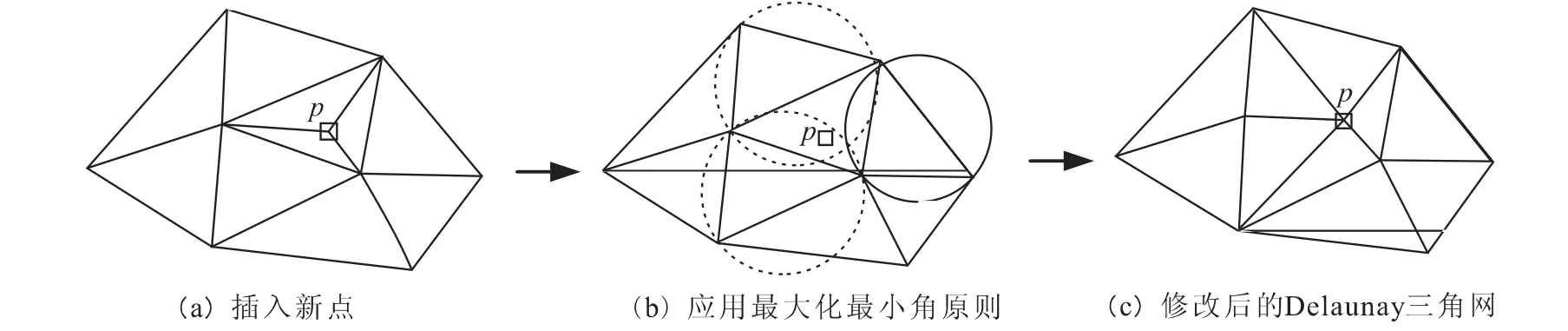
图1 局部优化过程LOP方法示意Fig.1 Sketch of local optimization process method.

Delaunay剖分是一种三角剖分的标准，实现它有多种算法，考虑到编码简易性以及算法执行的效率，本文对平面点集的Delaunay三角剖分采用以下的算法（图2）。（1）根据点集的坐标范围，求出点集的凸多边形外壳；（2）选择一个点，构造一个初始Delaunay三角网；（3）从集合中选择一个点，采用局部优化过程修改生成新的Delaunay三角网；（4）重复步骤3，直到所有点都计算完。

2 基于Delaunay三角剖分线性插值算法

基于Delaunay三角剖分的线性插值算法首先将输入的散点集合构建一个Delaunay三角网，然后循环将待插点加入已存在的Delaunay三角网从而实现插值运算。对于给定的一个Delaunay三角形的三个顶点的值fi（xi，yi），其中i＝1，2，3，待插点（x，y）处的值f（x，y）可以通过下式求得［6］：

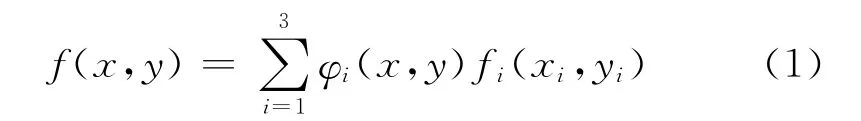
其中φi（x，y）是一个2－D的基函数，它是一个在顶点（xi，yi）处（此时值为1）线性变化到另一个顶点（xj，yj）（j≠i）（此时值为0）的函数。在实际计算中，可以将式（1）变换为

为了求取系数c＝ ［c1，c2，c3］T，可以根据已知的三个顶点fi（xi，yi）｛i＝1，2，3｝来联立线性方程组来求得：

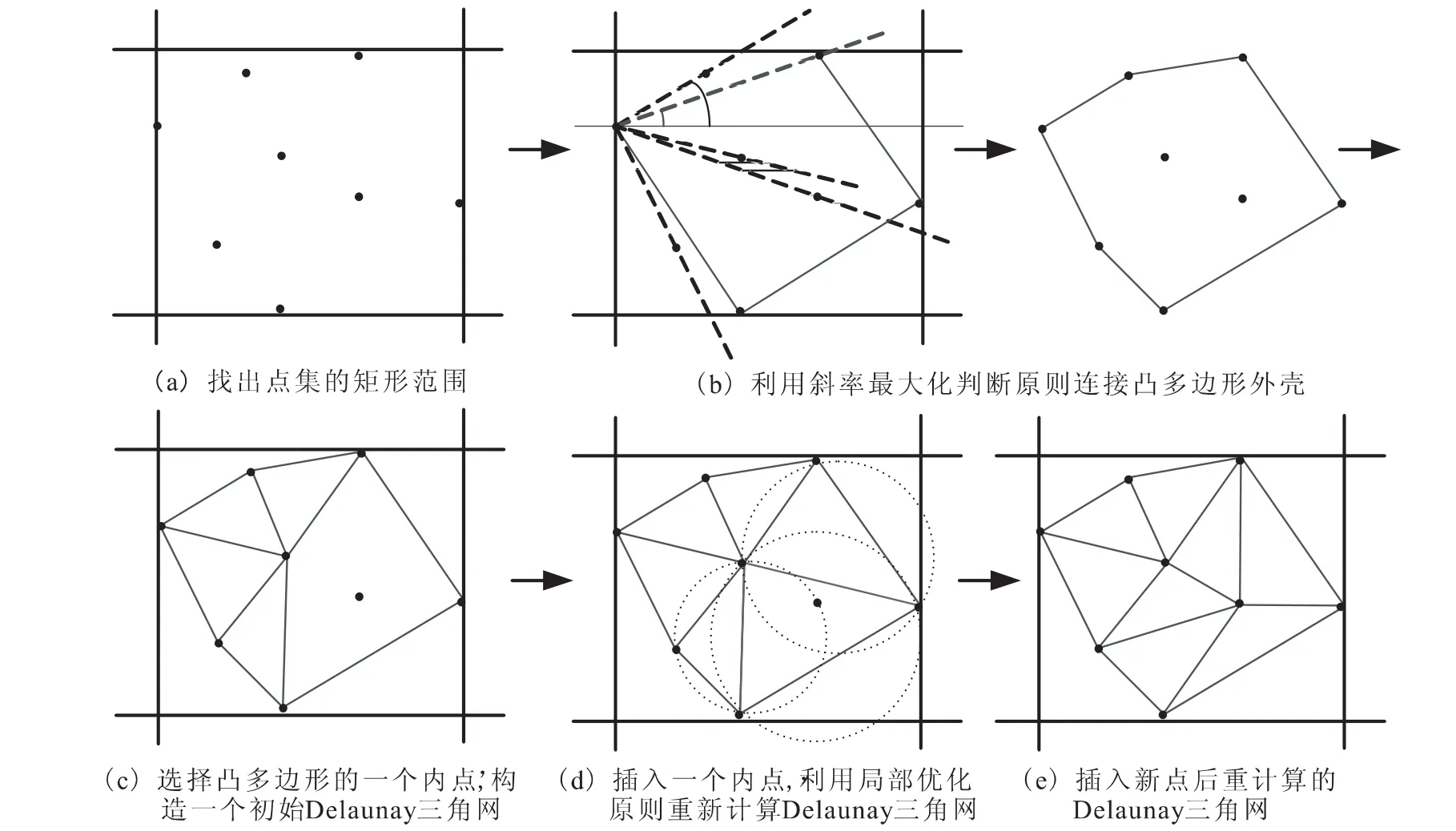
图2 平面上Delaunay三角剖分算法示意图Fig.2 Schematic diagram of Delaunay triangulations algorithm on the plane.

求解式（3）的线性方程组得出系数c＝ ［c1，c2，c3］T的值，然后利用式（2）便可求出待插点（x，y）处的值。

基于Delaunay三角剖分线性插值算法实现步骤如下：（1）输入平面上散点数据，构建Delaunay三角网；（2）输入待插点pi（x，y），查找pi所处的Delaunay三角形，计算c1，c2，c3，计算f（x，y）；（3）重复步骤（2）直到计算完所有待插点；（4）输出计算结果用于成图并结束程序。

3 应用实例

由于本文所实现的方法是基于Delaunay三角剖分的线性插值算法，因此它的主要优势在于插值效率，另一方面由于该算法并不外插，因此它另外一个优势在于便于网格化带地形特征的数据。Surfer中的自然邻点插值算法（NNI）也是基于Delaunay三角剖分的一种局部插值算法，它们具有较好的可比性，因此本文应用一个带地形的野外实测MT数据的反演结果作为例子，从插值精度上作定性的比较，插值效率上作定量的比较。

3.1 应用实例1

图3中的例子中原始数据共有7 960个散点数据，分别用本文算法（图3（a））和Surfer NNI算法（图3（b））用200×200来进行网格化处理。从图3中可以看出，本文的算法在插值精度和光滑度上要比Surfer NNI插值算法要略差一些，但是总体形态即插值结果基本一致，因此在既要兼顾到插值精度又要满足实时性的情况下，本文的算法是基本符合要求的。

图3 实例1本文算法和Surfer NNI算法插值结果比较Fig.3 Comparing of interpolation results between the algorithm of this paper and Surfer NNI in case 1.

为了定量的说明本文的插值算法的插值速度，对图3所示的例子分别用不同的网格密度对该数据进行网格化处理并和商业软件Surfer中速度较快的NNI插值算法进行对比，如表1所示。

表1 本文算法与Surfer NNI插值算法对比

从表1中可以看出，本文算法在速度上要优于Surfer NNI算法。同时可以看出，随着插值网格的密度增大，算法的耗时接近线性增加，因此本文的算法的速度相对NNI算法来讲更适合于实时性要求较高的场合。

3.2 应用实例2

图4中的例子中原始数据共有720个散点数据，分别用本文算法（图4（a））和Surfer NNI算法（图4（b））用400×400来进行网格化处理。从图4中可以看出，本文的算法插值结果在光滑度上要比Surfer NNI插值算法要略差一些，但是总体形态即插值结果基本一致。另外，在对带凸地形的插值效果上，两种插值算法也基本上一致，都能很好的模拟地形的起伏，都达到了满意的效果。但在算法速度上，本文的算法仅耗时0.02s，而Surfer NNI却花费4.95s。因此在对算法实时性要求较高，但精度基本能满足要求的情况下本文的算法具有较大的优势。

图4 实例2本文算法和Surfer NNI插值结果比较Fig.4 Comparing of interpolation results between the algorithm of this paper and Surfer NNI in case 2.

4 结论

本文实现的基于Denaulay三角剖分的插值算法稳定性好，速度快，并具有保真度高、便于网格化带地形特征的数据等优势，适用于MT等不规则分布数据的实时、快速网格化处理，是地球物理数据实时二维网格化最佳的插值方法之一。

［1］Watson D F.Contouring：aguide to the analysis and display of spatial data［M］.［S.l.］：Pergamon Press，1992.

［2］刘兆平，杨进，武炜.地球物理数据网格化方法的选取［J］.物探与化探，2010，34（1）：93－97.

［3］郭良辉，孟小红，等.地球物理不规则分布数据的空间网格化法［J］.物探与化探，2005，29（5）：438－442.

［4］赵文芳.离散点集Delaunay三角网生成算法改进与软件开发［J］.测绘工程，2003，12（04）：22－25.

［5］凌海滨，吴兵.改进的自连接Delaunay三角网生成算法［J］.计算机应用，1999，19（12）：10－12.

［6］文伟，杨耀权，于希宁.用Visual C语言实现的Delaunay三角剖分算法［J］.华北电力大学学报，2000，27（4）：54－58.

［7］徐青，常歌，杨力.基于自适应分块的TIN三角网建立算法［J］.中国图象图形学报，2000，5（6）：461－465.

［8］潘荣江，屠长河，孟祥旭，等.基于均匀网格的Delaunay三角网算法在随机聚合网屏中的应用［J］.中国图象图形学报 ，2002，7（5）：495－500.

［9］Q Fan，A Efrat，V Koltun，et al.Hardware－Assisted Natural Neighbor Interpolation［A］∥Proceedings of ALENEX［C］.2005：111－120.

［10］Sambridge M，Braun J，McQueen H.Geophysical parameterization and interpolation of irregular data using natural neighbors［J］.Geophysical Journal International 1995，12（2）：837－857.

［11］Lee D T，Schacheer B J.Two algorithms for constructing a Delaunay triangulation［J］.International Journal of Computer and Information Science，1980，9（3）：219－242.

［12］Lawson C L.Software for C surface interpolation［M］.New York：Academic Press，1997.

［13］Watson D F.Computing the n－dimension Delaunay tessellation with application to Voronoi polygons［J］.Computer Journal，1981，24（2）：167－172.

［14］徐凯军，石双虎，周家惠.三维大地电磁激电效应特征研究［J］.西北地震学报，2009，31（1）：31－34.

［15］李希亮，刘希强，董晓娜，等.高阶统计量方法在地球物理学中的应用与展望［J］.西北地震学报，2010，32（2）：201－205.