ZHANG Li-ting

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

The Morphic Properties of Subring-Extension

ZHANG Li-ting

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

LetRbe a ring,Cbe a subring ofR, and 1R∈C. Set

subring-extension; (left) morphic ring; strongly morphic

1 Introduction

In [1], Nicholson and Sánchez Campós introduced and studied left morphic rings, which were extensively studied in the literatures[2-7]. An elementain a ringRis called left morphic ifR/Ra≅l(a). A ringRis called left morphic in case every element inRis left morphic. Right morphic rings are defined analogously. It is well known thatais left morphic in a ringRif and only if there exists someb∈Rsuch thatRa=l(b) andRb=l(a). In [2], the authors investigate when the trivial extensionR∝Mof a ringRand a bimoduleMoverRis (left) morphic. In this paper, we introduce a new extension ring of a ringR-subring-extension, and investigate the relation between the morphic property ofRand its subring-extension.

2 Subring-extensions

ProofFor anya∈C, we have (a,0)∈Sis left morphic. Then there exists (b,c)∈Ssuch thatlS(a,0)=S(b,c) andlS(b,c)=S(a,0). We can easily to verify thatlC(a)=CbandlC(b)=Ca. ThusCis a left morphic ring.

Analogously, for anyy∈R, we have (0,y)∈Sis left morphic. Then there exists (x,t)∈Ssuch thatlS(0,y)=S(x,t) andlS(x,t)=S(0,y). It is clear thatRy⊆lR(x+t) andR(x+t)⊆lR(y). Next, letm∈lR(x+t). It follows that (0,m)∈lS(x,t), and so (0,m)∈S(0,y). Immediately we getm∈Ry, whenceRy=lR(x+t). And letn∈lR(y), we derive (0,n)∈lS(0,y)=S(x,t), say (0,n)=(h,r)(x,t) for some (h,r)∈S. Then 0=hxandn=ht+r(x+t). Son=h(x+t)+r(x+t)=(h+r)(x+t)∈S(x+t). HenceR(x+t)=lR(y). The proof is complete.

The following example shows that the converse of Corollary 1 is not true.

Proposition2LetRbe a ring, and leta∈R. Then the following are equivalent:

(1)a∈Ris left morphic.

(1)⟹(2) Sincea∈Ris left morphic, then there existsb∈Rsuch thatlR(a)=RbandlR(b)=Ra. It can be verified thatlS(a,0)=S(b,0) andlS(b,0)=S(a,0).

(2)⟹(1) If (a,0)∈Sis left morphic, it follows thatlS(a,0)=S(b,c) andlS(b,c)=S(a,0) for some (b,c)∈S. It is easy to verify thatlR(a)=RbandlR(b)=Ra, as required.

Lemma1LetRbearing anda,b∈R,u∈U(R). Then the following are equivalent:

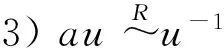
ProofBy [7, Lemma 3].

ProofSinceeis an idempotent inR, then (0,e) is an idempotent inS, and so (0,e)∈Sis left morphic. We know (0,eu)=(0,e)(u,0) and (0,ue)=(u,0)(0,e) where (u,0)∈U(S), so (0,eu) and (0,ue) are both left morphic inS.

Lemma2If eachCiis a subring of the ringRi, fori=1,2,…,n, then

ProofThe map

defined by

is the required ring isomorphism.

ProofThe map

defined by

is the required ring isomorphism.

4) Ifa≠0 andb≠-a, then we claim (a,b)∈Sis invertible. In fact, (a,b)(a-1,-(a+b)-1ba-1)=(a-1,-a-1b(a+b)-1)(a,b)=(1,0). This implies (a,b) is morphic inS, as required.

a) If allaij=0, butblm≠0 for somelandm. Again, by a series of elementary operations,xlmcan be moved to the (1,1)-entry, and all entries in the first row and the first column, except the (1,1)-entry, can be reduced to 0.

b) If allaij=-bij≠0. We can also take proper elementary operations, such that all entries in the first row and the first column, except the (1,1)-entry can be reduced to 0.

c) If there are bothaij=0 andalm=-blm≠0 for somei,j,landm. First, we movexij=(aij,bij)=(0,bij) to the (1,1)-entry, and by a series of elementary operations, we can change all the (1,k)-entries and (k,1)-entries fork>1 which have the formation (0,b1k) and (0,bk1) to 0. Second, movexlm=(alm,blm)=(alm,-alm) to the (1,1)-entry, then we can change all the (1,k)-entries and (k,1)-entries fork>1 which have the formation (a1k,-a1k) and (ak1,-ak1) to 0.

Hence,Xcan be reduced to

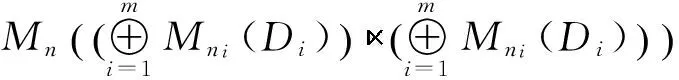
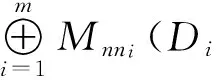
Corollary4IfRis a semisimple ring, thenRis strongly morphic.

For further study, we end this article by several problems.

[1] Nicholson W K, Sánchez Campós E. Rings with the dual of the isomorphism theorem[J]. J Algebra,2004,271(1):391-406.

[2] Chen Jianlong, Zhou Yiqiang. Morphic rings as trivial extensions[J]. Glasg Math J,2005,47(1):139-148.

[3] Chen Jianlong, Li Yuanlin, Zhou Yiqiang. Constructing morphic rings[C]//Advance in Ring Theory, Najing: Hackensack,2005:26-32.

[4] Lee T K, Zhou Yiqiang. Morphic rings and unit regular rings[J]. Journal of Pure and Applied Algebra,2007,210(2):501-510.

[5] Huang Qinghe, Chen Jianlong. π-morphic rings[J]. Kyungpook Math J,2007,47:363-372.

[6] 许秀玲，储茂权.关于Morphic环的推广[J].安徽师范大学学报：自然科学版,2008,31(6):522-524.

[7] Lee T K, Zhou Yiqiang. Morphic rings and unit regular rings[J]. Journal of Pure and Applied Algebra,2007,210(2):501-510.

[8] 葛平红，储茂权.单位正则环和SF-环[J].安徽师范大学学报：自然科学版,2009,32(4):322-324.

子环扩张的morphic性质

张丽婷

(杭州师范大学理学院，浙江 杭州 310036)

子环扩张；(左)morphic环；强morphic

10.3969/j.issn.1674-232X.2011.02.004

date： 2010-03-02

Supported by National Natural Science Foundation of Zhejiang Province (Y6090404); Supported by the Graduate Innovation Seed Project of Hangzhou Normal University.

Biography： ZHANG Li-ting(1986—), female, born in Zigong, Sichuan province, master, engaged in non-commutative ring theory. E-mail: zhangting138137@126.com

16E50;14F99MSC2010O153.3ArticlecharacterA

1674-232X(2011)02-0109-05