侯爱民 郝志峰 胡传福 陆海鹏

(华南理工大学计算机科学与工程学院，广东广州510006)

在研究图论的问题中，经常需判断两个图是否同构，即从顶点和边的拓扑结构上来看，两个图是否有可能以同样的方式画出.换句话说，当两个图同构时，两个图的顶点之间具有保持相邻关系的一一对应.判断两个图是否同构是一个NP难问题.

至今为止，国内国际上公认的实际可行的判断算法分为两类:一类是对顶点编号进行特殊处理［1-2］，另一类是通过不断删除顶点来对顶点集合的划分进行细分［3-7］.Babai等［1］使用顶点度数对随机图进行规范标记，能产生同样规范标记的两个图是同构的，不能产生同样规范标记的两个图是不同构的.该算法的时间复杂度为O(n2)，是目前为止运算速度最快的著名算法.其缺点是对于不能进行规范标记的两个图，算法失效;而且拒绝率上界为n－1/7.对其改进的算法［2］也具有非零非负的拒绝率，即虽然它们的平均运行时间非常快，也不能处理所有类型的图.顶点集合划分是判断图同构的一种有效方法，可以有效减小同构函数候选集.这一思想也是目前许多常见的图同构判断算法［3-7］的基本思想.但这些算法不可避免地都要进行回溯，也就是要构造一棵搜索树，不断进行试探和剪枝，算法的时间复杂度取决于回溯的深度和次数.

文献［8］中提出了判断无向图同构的一个高效的必要条件，使用这个条件，可以更细地对顶点集合进行划分.文献［9］中提出了判断无向图同构的一个充分必要条件，使用这个条件，可以判断同构的两个图在新增顶点和关联边后构成的新图是否同构.因为新图是否同构取决于旧图的同构函数，所以利用必要条件筛选旧图的同构函数候选集，可以降低时间开销.文中采用基于子图同构判断父图同构的策略，提出一种新的无需回溯的快速算法，用于降低时间开销，保证正确判断.通过理论论证、实际案例测试，验证了该算法的有效性.

1 无向图同构的相关理论

使用必要条件可以对顶点集合V(G)进行划分.针对某种划分{cell1，cell2，…，cellk}，(celli⊆V(G)，1≤i≤k)，同构函数候选集的大小为.必要条件不同，导致顶点集合划分的细分程度不同.细分程度越细(即k越大，且越小)，同构函数候选集越小，从而导致需检验的顶点对应关系越少，越能有效地降低判断算法的时间开销.文献［8］中提出一个必要条件，其细分程度比“顶点度”必要条件和“顶点的邻接点的度序列”必要条件更细，也比文献［3］中提出的必要条件更细.

本算法核心思想使用文献［9］中提出的充分必要条件进行判断，既可以保证完备性和收敛性，又可以避免回溯.

定义1［8］设无向图G=(V，E)，在其邻接矩阵AG=(aij)n×n中，第i行与第j行的行码距异或距离定义为第i行与第j行对应列上取不同值(即一个取0，另一个取1或k)的诸列上各元素之和，记为xord(i，j).如果 i≠j，则令 byij=xord(i，j);否则令byij=aii.称矩阵BYG=(byij)n×n为图 G 的行码距异或矩阵.

定义2［8］设无向图G=(V，E)，在其邻接矩阵AG=(aij)n×n中，第i行与第j行的行码距同或距离定义为第i行与第j行对应列上取相同值(即一个取1或k，另一个也取1或k)的诸列上各元素之和，记为aord(i，j).对于所有的 i和 j，令 btij=aord(i，j).称矩阵BTG=(btij)n×n为图G的行码距同或矩阵.

定义3［8］设两个矩阵 A=(aij)n×n和 B=(bij)n×n，A 中的行编号为 u1，u2，…，un，B 中的行编号为 v1，v2，…，vn.如果存在一个置换［u1↔ v'1，u2↔v'2，…，un↔ v'n］，其中(v'1，v'2，…，v'n)是(v1，v2，…，vn)的一种排列，使得A中编号为ui的行与B中编号为v'i的行具有元素一样的特征(不考虑元素的位置次序)，则称［u1↔v'1，u2↔v'2，…，un↔v'n］为矩阵 A 和 B的行－行置换.

定理1［8］设两个无向图G和H同构，则图G的邻接矩阵、行码距异或矩阵、行码距同或矩阵分别与图H的邻接矩阵、行码距异或矩阵、行码距同或矩阵具有同一的行－行置换.

定理2［8］设两个无向图G和H同构，则一定存在图G的一个子图Gi和图H的一个子图Hj同构.对于任意一对同构的子图Gi和Hj，必有图Gi的邻接矩阵、行码距异或矩阵、行码距同或矩阵分别与图Hj的邻接矩阵、行码距异或矩阵、行码距同或矩阵具有同一的行－行置换.这种关系一直保持到Gi和Hj只有两个顶点.

定理3［9］同构的两个无向图G和H，各自增加一个顶点unew和vnew，以及与新增顶点关联的若干条边，形成两个新图G+unew和H+vnew.新图G+unew和H+vnew同构，当且仅当存在G≅H的一个同构函数f，使得新顶点的所有邻接点在同构函数f的作用下，在G和H中保持同构关系.

2 无向图同构的快速判断算法

步骤1 根据图G和H的邻接矩阵AG和AH，分别计算图G和H的行码距异或矩阵BYG和BYH，以及行码距同或矩阵BTG和BTH.

步骤2 根据图G的行码距异或矩阵BYG，依次考虑每个顶点ui(1≤i≤n)所在的行.对于每个顶点ui所在的行，在图H的行码距异或矩阵BYH中寻找保持元素一样的对应行，构成顶点ui的一个匹配集S_ui.如果某个顶点不存在匹配集，则可以判断图G和H不同构，算法结束;如果所有匹配集的并集没有n个元素，则可以判断图G和H不同构，算法结束;否则，在邻接矩阵AG和AH、行码距同或矩阵BTG和BTH中，检查这些匹配集是否依然成立.如果不成立，则可以判断图G和H不同构，算法结束;否则，根据匹配集，生成若干个行－行置换.

步骤3 考虑图G的任意一个顶点ui.对于vj∈S_ui，依据步骤1和步骤2的方法，判断子图G－ui和H－vj是否同构.如果存在某个顶点ui，使得对于vj∈S_ui，都有子图G －ui和H －vj不同构，则可以判断图G和H不同构.算法结束.

步骤4 考虑图G的具有相同最小度数的每个顶点ui.对于vj∈S_ui，分别判断子图G －ui和H －vj是否为完全图.若是，则可以判断图G和H同构.算法结束.此时，G－ui≅H－vj的任何同构函数f，补充对应关系vj=f(ui)后，都将构成G≅H的同构函数.

步骤5 考虑图G的具有相同最小度数的每个顶点ui.对于vj∈S_ui，检查ui的所有邻接点和vj的所有邻接点在子图G－ui和H－vj中是否保持同构关系.具体做法如下根据子图G－ui和H－vj的顶点匹配集，检查ui的所有邻接点和vj的所有邻接点是否满足这些匹配关系;在满足的前提下，根据排列组合生成若干个行－行置换，这些行－行置换构成一个潜在的同构函数候选集;检查每一个行－行置换是否是子图G－ui和H－vj的同构函数;如果有一个行－行置换是子图G－ui和H－vj的同构函数f，则可以判断图G和H同构.算法结束.此时，对这个同构函数f补充对应关系vj=f(ui)后，将构成G≅H的同构函数.否则，所有的行－行置换都不是子图G－ui和H－vj的同构函数，可以判断图G和H不同构，算法结束.

3 实验及案例分析

文中给出了一些典型案例(见图1)来说明上述算法的可行性，同时给出了与其它必要条件/算法的对比分析，以说明上述算法的有效性.

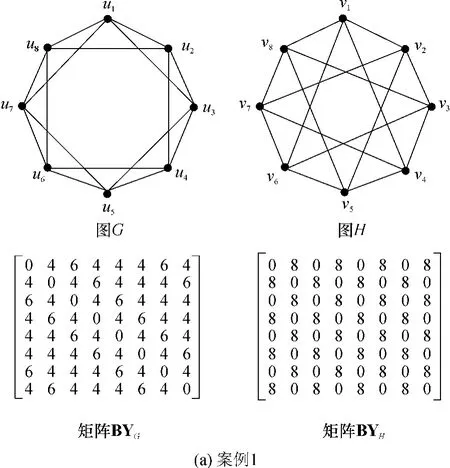
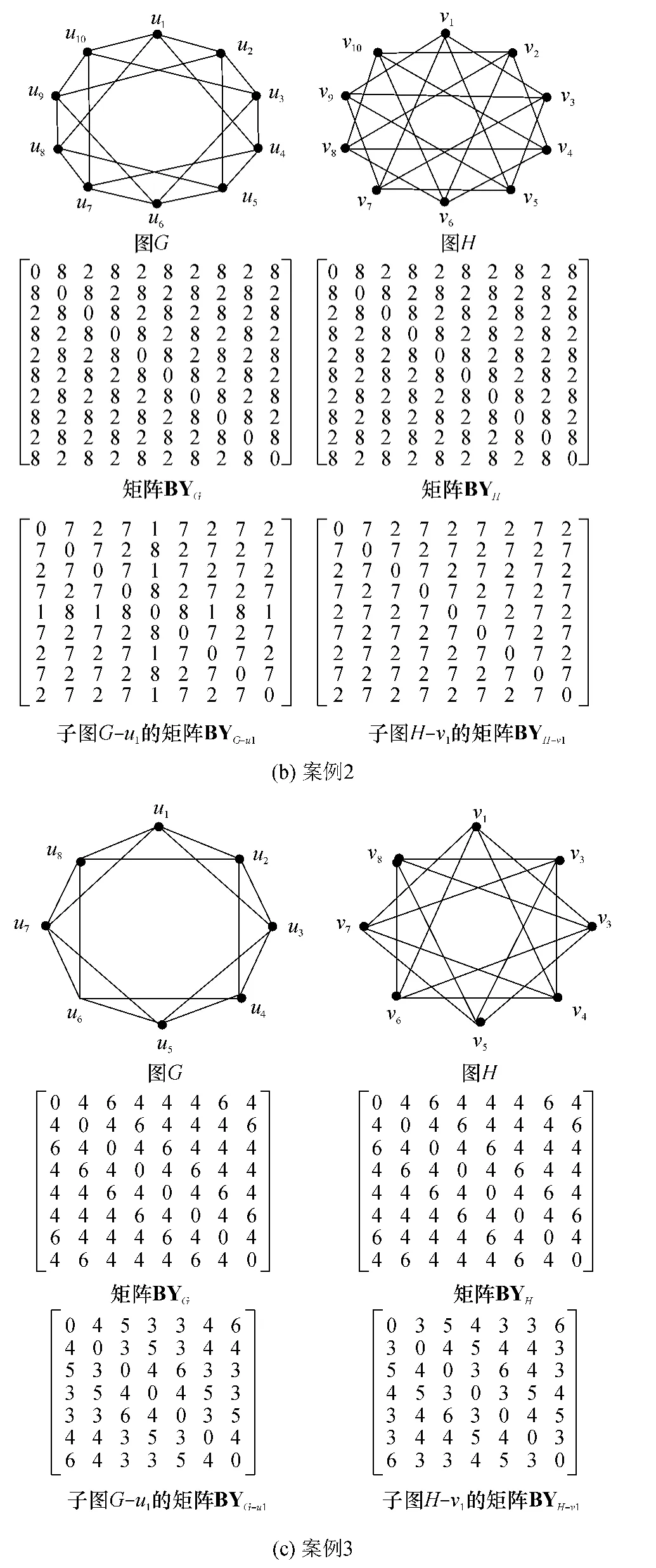
图1 一些典型案例Fig.1 Some typical cases

如图1(a)所示，案例1中，原始图G和H的行码距异或矩阵BYG和BYH之间不存在同一的行－行置换，因为BYG中存在一行(04644464)，在BYH中不存在对应行.相反，使用“顶点度”必要条件和“顶点的邻接点的度序列”必要条件，以及文献［3］中提出的必要条件，都不能直接判断出G和H不同构.此外，文献［1］中提出的算法不能对图1(a)案例进行规范标记，从而无法判断是否同构.

如图1(b)所示案例2中，原始图G和H的行码距异或矩阵BYG和BYH之间存在同一的行－行置换，但是子图G－u1的行码距异或矩阵BYG－u1和子图 H－vj(1≤j≤10)的行码距异或矩阵BYH－vj之间不存在同一的行－行置换.使用“顶点的邻接点的度序列”必要条件，能直接判断出G－u1和H－vj(1≤j≤10)不同构.但使用“顶点度”必要条件和文献［3］中提出的必要条件，都不能直接判断出G－u1和H－vj(1≤j≤10)不同构.另一方面，在处理图1(b)案例时，文献［3-7］中算法需要进行多次回溯操作.此外，文献［1］中提出的算法不能对图1(b)案例进行规范标记，从而无法进行判断.

此外，文献［1-2］是目前为止平均时间开销最少的判断算法，其缺点是具有非零非负的拒绝率.也就是说，这类算法不能处理所有类型的图.例如，文献［1］中的拒绝率上界为n－1/7.针对顶点个数n=128的两个无向图，最坏情况下将有50%的图不能进行判断，而文中算法可以处理所有类型的图.

事实上，对随机生成的无向正则图和无向非正则图、无向强正则图、无向伪图等进行案例验证，都能证明了文中算法的正确性和有效性.限于篇幅所限，不再赘述.

使用C语言编程实现上述图同构判断算法，对随机生成的一对随机图(包括正则图和非正则图)，以及图数据库［10］中的11900个样本进行程序判定.这些样本共分5大类，根据顶点个数和其它参数，每个大类又分为若干子类.每个子类测试了100个样本，即50个配对图.所有实验均在AMD Athlon(tm)64×2 Dual Core Processor 3600Hz/1GB内存的计算机上进行，结果如表1所示.测试结果表明，无一例外，对于同构的两个图，文中算法均能正确判断，并给出同构函数;对于不同构的两个图，也能正确判断，且用时合理.

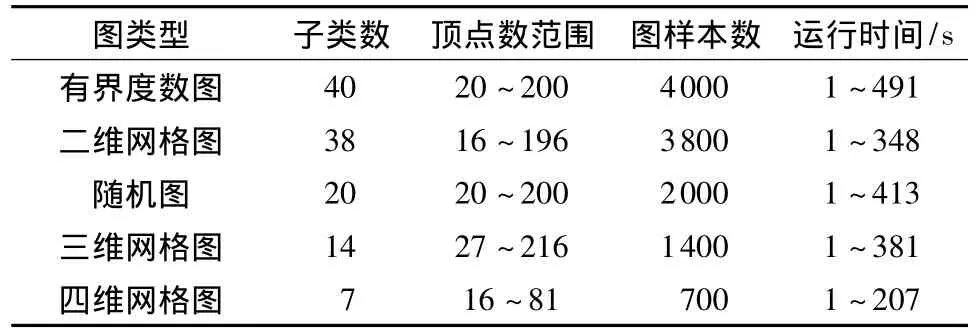
表1 图同构判断算法对5种典型类型图的测试结果Table 1 Test results of the five categories by the proposed graph isomorphism algorithm

程序运行的实验数据表明:对于同构的两个图，可以在100s之内判断同构，找到一个同构函数.对于不同构的两个图，运行时间取决于顶点个数和正则性.在顶点个数相同的情况下，非正则图的运行时间少于正则图的运行时间.顶点个数越多，运行时间越长.强正则图的运行时间最长.这些结论与实际案例验证的结果一致.

4 结论

无向图同构的判断问题至今没有完全解决.规范标记算法具有O(n2)的时间复杂度，但是不完备，不能处理所有类型的图.顶点划分算法需要不断地回溯和试探，从而造成最坏情况下指数阶时间复杂度.为了避免回溯，同时保证完备性，文中提出一种基于充要条件的快速判断算法.为了进一步降低时间开销，采用基于子图同构判断父图同构的策略，使用一种高效的必要条件筛选同构函数候选集的范围.最后通过理论论证、实际案例测试，验证了该算法的有效性.

［1］Babai L，Erds P，Selkow S M.Random graph isomorphism［J］.SIAM Journal of Computing，1980，9(3):628-635.

［2］Czajka Tomek，Pandurangan Gopal.Improved random graph isomorphism ［J］.Journal of Discrete Algorithms，2008，6(1):85-92.

［3］Ullmann J R.An algorithm for subgraph isomorphism［J］.Journal of the Association for Computer Machinery，1976，23(1):31-42.

［4］Schmidt D C，Druffel L E.A fast backtracking algorithm to test directed graphs for isomorphism using distance matrices［J］.Journal of the Association for Computer Machinery，1976，23(3):433-445.

［5］McKay B D.Practical graph isomorphism［J］.Congressus Numberantium，1981，30:45-87.

［6］Cordella L P，Foggia P，Sansone C，et al.An improved algorithm for matching large graphs［C］∥Proceedings of International Workshop on Graph-based Representation in Pattern Re-cognition.Ischia:［s.n.］，2001:149-159.

［7］Cordella L P，Foggia P，Sansone C，et al.Subgraph transformations for the inexact matching of attributed relational graphs［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26(10):1367-1372.

［8］侯爱民.图同构的矩阵初等变换判定及算法设计［J］.计算机工程与应用，2006，42(20):51-54.Hou Ai-min.Elementary operations on a matrix to determine the isomorphism of graphs［J］.Journal of Computer Engineering and Applications，2006，42(20):51-54.

［9］侯爱民.图同构的一个充分必要条件［J］.计算机工程与应用，2009，45(30):57-61.Hou Ai-min.Necessary and sufficient condition of graphic isomorphism ［J］.Journal of Computer Engineering and Applications，2009，45(30):57-61.

［10］Foggia P，Sansone C，Vento M.A Database of graphs for isomorphism and sub-graph isomorphism benchmarking［C］∥Proceeding of the 3rd IAPR-TC15 International Workshop on Graph-based Representions.Berlin:Springer，Italy，2001:176-187.