黄湧辉

（华南师范大学 数学科学学院，广东 广州 510631）

一类改进的高斯-赛德尔迭代法的比较性定理

黄湧辉

（华南师范大学 数学科学学院，广东 广州 510631）

讨论了改进的高斯-赛德尔迭代法的收敛性.若系数矩阵为非奇异不可约M-矩阵，则该预条件下高斯-赛德尔迭代法收敛的快慢取决于原高斯-赛德尔迭代法谱半径的大小.同样，在该预条件下高斯-赛德尔迭代法的谱半径大小与其他高斯-赛德尔迭代法的谱半径大小有关.

谱半径；预条件迭代法；非奇异不可约M-矩阵；收敛速度；高斯-赛德尔迭代法

考虑线性方程组

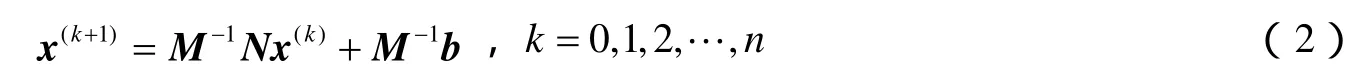
其中称 M-1N为方程（1）的迭代矩阵，迭代格式（2）是否收敛取决于迭代矩阵 M-1N.

一般地，对线性方程组（1）的系数矩阵A做如下的分裂

其中D为非奇异对角矩阵、L为严格下三角矩阵、U为严格上三角矩阵.

为讨论方便，当A可逆时，通过初等变换把A的对角元都化简为1，因此

对于形如式（3）的系数矩阵，Gauss-Seidel迭代法的迭代矩阵为： G =(I -L )-1U.虽然迭代法是求解线性方程组的主要方法，但是当系数矩阵的条件数较大时，系数矩阵对于求解线性方程组是病态的，此时迭代法会出现不收敛和收敛速度慢的情况；对于迭代法收敛速度慢的问题，采用适当的预处理技术，可以使系数矩阵的特征值分布更加集中，降低矩阵的条件数，改良矩阵的病态特性.

线性方程组（1）两端左乘可逆矩阵 P ∈Rn×n，使方程组等价地转换为预条件的方程组

通常称可逆矩阵P为预处理矩阵（或预处理因子），则与式（2）对应的基本迭代形式为：

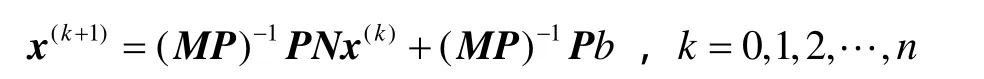
其中 PA = PM -PN是PA的分裂，且PM是可逆的.

本文主要考虑：对于线性方程组（1），如何选取预处理矩阵P，使得用Gauss-Seidel迭代法解经过预处理后的方程组（4）有更快的收敛速度.

考虑用一类新的预处理方法解线性方程组（1），取

用Pα左乘线性方程组（1）的两边，得

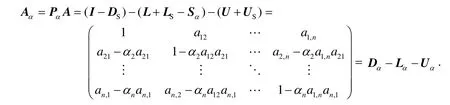
其中Dα、Lα、Uα分别为Aα的主对角元，下三角元和上三角元.

此时，预条件Gauss-Seidel迭代法的迭代矩阵为

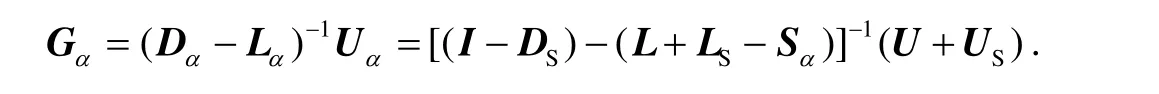
1 预备知识

定义1[2]33设则称 Zn×n的矩阵A为Z-矩阵；如果A是Z-矩阵，满足A=sI-B，B≥0，实数s＞0且谱半径 ρ(B)≤ s ，称A是M-矩阵.特别地，当 ρ(B)＜s 时，称A为非奇异M-矩阵.

定义2[2]1设n阶方阵A≥0，如果存在一个置换矩阵使得其中B、 D是分别是k、l阶方阵（k≥1、l≥1），则称A是可约矩阵，否则称A是不可约矩阵.

定义3[3]37设A是n阶方阵，A有分裂A=M-N，其中M为非奇异矩阵，若 ρ(M-1N )＜1，则称这个分裂是收敛的；又若M是非奇异的M-矩阵且N≥0，则称这个分裂为M-分裂.

引理1[4]232若矩阵A是不可约的，A=M-N为矩阵A的一个M-分裂，则存在一个向量x＞0，使得M-1Nx =ρ(M-1N) x成立.

引理2[2]4设A是n阶不可约非负矩阵，则有：

i）若存在x≥0，x≠0满足 Ax ≥αx，则 ρ(A)≥a ；

ii）若存在x≥0，x≠0满足Ax≤βx，则ρ(A)≤β.

引理3[4]231设A是Z-矩阵，则A是一个非奇异M-矩阵的充要条件是是一个非奇异M-矩阵，其中

2 主要结论

定理1 若线性方程组（1）的系数矩阵A是非奇异不可约M-矩阵，用G表示系数矩阵A的Gauss-Seidel迭代法的迭代矩阵，Gα表示经预条件 Pα=I +Sα后的Gauss-Seidel迭代法的迭代矩阵，对任意有下列结论成立：

1）当0 ＜ ρ(G)＜1时， ρ(Gα) ≤ρ(G)；

2）当 ρ(G)=1时， ρ(Gα) =ρ(G)；

3）当 ρ(G)＞1时， ρ(Gα) ≥ρ(G).

证明 由于系数矩阵A是非奇异不可约M-矩阵，且 A =（ I- L） -U为矩阵A的一个M-分裂，G =(I -L )-1U，则由引理1知，存在一个正向量x，使得 Gx =ρ(G) x，由引理3知是一个非奇异M-矩阵.

定理2 若线性方程组（1）的系数矩阵A是非奇异不可约M-矩阵，设γ≤β，其中γ = (γ1, γ2,… ,γn)， β =（β1, β2,…,βn） 且 γi∈ ［0,1］、 βi∈ ［0,1］,∀ i= 2,3,… ,n ，即 ∀i = 2,3,…,n,γi≤βi，分别用Pγ=I+Sγ和Pβ=I +Sβ预处理矩阵A后得到Gauss-Seidel迭代矩阵分别为Gγ和Gβ，对于任意 αi∈有下列结论成立：

1）当0 ＜ρ(Gγ)＜1时，ρ(Gβ) ≤ρ(Gγ)；

2） ρ(Gγ)=1时， ρ(Gβ) =ρ(Gγ)；

3）当 ρ(Gγ)＞1时， ρ(Gβ) ≥ρ(Gγ).

证明 由于系数矩阵A是非奇异不可约M-矩阵，由引理3得： Aα=(I +Sα)A也是非奇异不可约M-矩阵，由于则Aα=Dα-Lα-Uα为矩阵Aα的一个M-分裂则由引理1知，存在一个正向量x，使得令由定理1知：

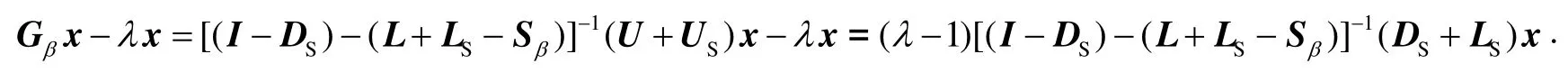
3 数值例子

以上分析表明：在一定条件下预条件能够加快Gauss-Seidel迭代法的收敛速度.下面举例说明该预条件的优越性.

3.1 预条件 Pα =I +Sα加快Gauss-Seidel迭代法的收敛速度

为了方便计算，取 α2=α3=α4. αi(i = 2,3,4)取不同的值时， ρ(G)与 ρ(Gα)的比较如表1所示.

表1 αi( i = 2,3,4)取不同的值时，ρ(G)与 ρ(G α )的数值

ρ(G)的是 ρ(Gα)的一个特例，因为 G =(I -L )-1U本身是不含参数 αi(i = 2,3,4)，它不会受到参数αi(i = 2,3,4)的影响，当 αi(i = 2,3,4)=0.1~0.9时，ρ(G)= 0.6347，且ρ(G ) ＞ρ(Gα).即预条件 Pα= I+Sα能够加快Gauss-Seidel迭代法的收敛速度.

3.2 预条件下Gauss-Seidel迭代法的谱半径是单调下降的

为了方便计算，取 β2=β3=β4.用Pα=I+Sα和Pβ=I +Sβ预处理矩阵A后得到Gauss-Seidel迭代矩阵分别为Gα和Gβ. αi、 βi(i = 2,3,4)取不同的值时， ρ(Gα)、 ρ(Gβ)的比较如表2所示.

表2 αi, β i (i = 2,3,4)取不同的值时， ρ(G α )与 ρ(Gβ )的数值

由表2，当β＞α有 ρ(Gβ) ＜ρ(Gα)，即预条件下Gauss-Seidel迭代法的谱半径单调下降.

[1]KOHNO T,KOTAKEMORI H,NIKI H.Improving modified iterative methods for Z-matrices[J].Liner Algebra and Its Application,1997,267:113-123.

[2]黄廷祝，杨传胜.特殊矩阵分析及应用[M].北京：科学出版社，2007:1-33.

[3]宋永忠.线性方程组迭代解法[M].南京：南京师范大学出版社，1992:37.

[4]LI Wen,SUN Weiwei.Modified Gauss-Seidel type methods and Jacobi type methods[J].Linear Algebra and Its Application,2000,317:227-240.

A New Comparison Theorem for the Preconditioned Gauss-Seidel Iterative Method

HUANG Yong-hui
(School of Mathematical Sciences,South China Normal University,Guangzhou 510631,China)

In this paper,the convergence analysis for a new preconditioned Gauss-Seidel iterative method wasdiscussed.Ifthe coefficientmatrix isa nonsingularirreducibleM-matrix,the convergence rate of this iterative method depends on the spectral radius of the original Gauss-Seidel method.Likewise,the spectral radius of the preconditioned Gauss-Seidel iterative method also depends on one of the preconditioned Gauss-Seidel methods.Finally,some numerical examples are given to explain our theoretical results.

spectral radius;preconditioned iterative method;nonsingular irreducibleM-matrix; convergence rate;Gauss-Seidel iterative

?

O241.6

A

1006-7302（2011）03-0019-04

2011-02-08

黄湧辉（1989—），男，广东揭阳人，研究方向为计算数学.