基于双向搜索的运输路线优化算法

2010-12-15贾珺孙静瑜侯冰

军事运筹与系统工程 2010年4期

贾珺，孙静瑜，侯冰

（1.军事科学院军事运筹分析研究所，北京100091；2.军事科学院军队建设研究部，北京100091；3.总装备部电子信息部电子局，北京100034）

1 引言

在后勤补给的运筹研究中运输路线的优化问题是一个很有代表性的问题，它具体是指当从某基地向某阵地运送物资时，如果有多条路线可选择，通过给定每条道路的最大通过能力，即单位时间内所能通过的最大车辆数目及通过代价（如长度、时间等），确定一条运输路线，使得所走的路程为最短或者在给定时间内通过的车辆数目最大，或者在代价最小的条件下通过的车辆数目最多[1]。其中所走的路程为最短这个问题可以转换为通过的路程最短、耗费的时间最短或造成的损失最小等，是运输路线优化研究中应用最为广泛的。

2 运输路线有向图化简

运输路线的数字化指的是将一个物理的运输路线图转变为计算机可以识别和处理的数据类型。在图论中大量使用的简单有向图是不包含环和平行边的有向图，它可以作为运输路线图的抽象表示，这一步抽象工作一般为人工完成，也可以使用模式识别和计算机图形学的方法通过计算机辅助完成。构建好的有向图可以将其点和边的关系用关联矩阵的方式表示出来。

2.1 运输路线有向图的构建

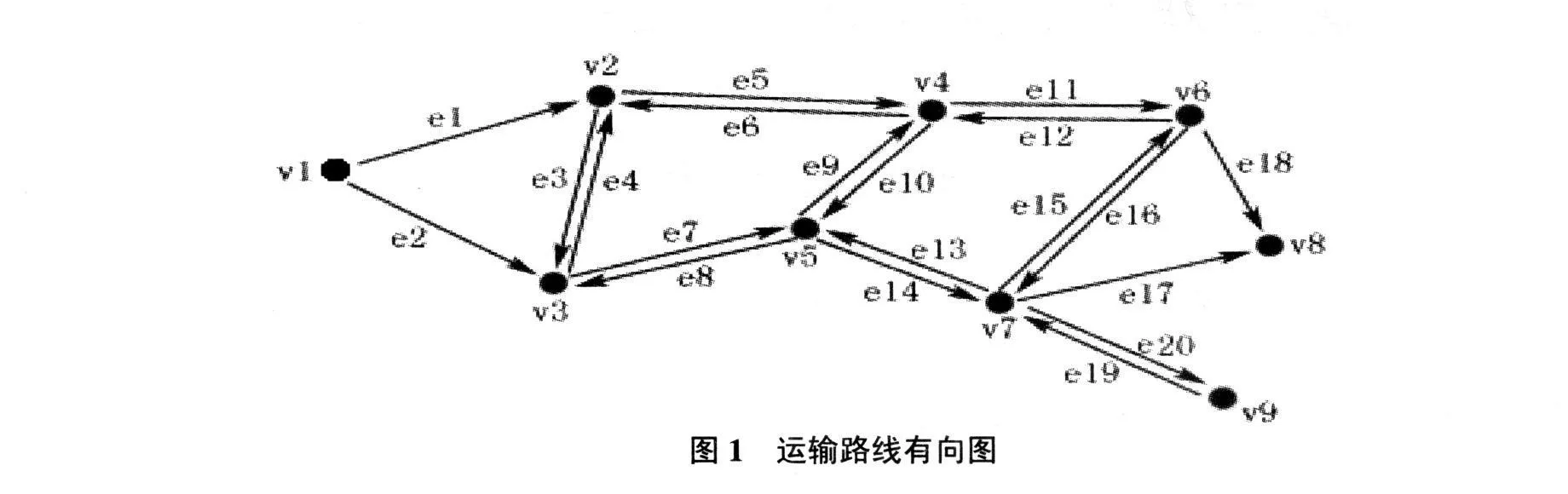
通常在运输路线的优化问题中是将运输路线抽象为无向图，因为从实际考虑，两个点之间如果有道路相连，在不考虑特殊因素的条件下其应该是双向互通的，但是对于一次实际的后勤补给运输来说，从起点出发到终点结束，在计算最短路径的情况下肯定不会出现在任意两个端点之间的往返运动。例如，如果对于路线1：v1v2v3v2v4为一条路径，那么路径2：v1v2v4必存在且长度要小于路径1；在某些特定条件下，某两个端点可能存在单向连通，所以利用有向图构建运输路线更加符合实际情况。综上，可以将运输路线抽象化为起点只有出度而终点只有入度的有向图，其余端点之间的关系以实际情况决定。如图1所示，其中V={v1，v2，…，v9}为顶点集，E={e1，e2，…，e20}为边集，v1为运输路线的起点，v8为运输路线的终点。由上面分析可知，生成的最短路径应该是基于图G的一个初级通路v1…v8，即没有重复顶点的通路。

2.2 关联矩阵的构建及化简

运输路线有向图为G=＜V，E＞，其中V={v1，v2，…，vn}为顶点集，n为顶点个数，E={e1，e2，…，em}为边集，m为边的条数。图G的关联矩阵=1，2，…，n，j=1，2，…，m。

下面给出悬挂点和悬挂边的定义。设vi（i=1，2，…，n）∈V，且vi不是运输路线的起点或终点，当以下任一种情况出现时，称vi为悬挂点：①M的行向量Mi中仅存在一个非零值mij，mij=1或mij=—1（j=1，2，…，m）；②M的行向量Mi中仅有一对非零值mij和mik，mij=1，mik=—1（j、k=1，2，…，m，j≠k），且存在vl（l=1，2，…，n，l≠i）∈V，使得mlj+mlk=0，mlj≠0，mlk≠0。当vi为悬挂点时，与vi相连的边ej为悬挂边，即满足mij≠0的边ej为悬挂边。

针对图1，关联矩阵是一个9×20的矩阵，如下：

根据上面的定义，v9为图1中的悬挂点，e19、e20为悬挂边。如果在最短通路中有v9，其必然存在一个往返的过程，因此生成的最短路径的初级通路肯定与v9、e19、e20不相关，可以在关联矩阵中删掉与v9相关的行、与e19和e20相关的列，将关联矩阵化简为8×18的矩阵。

经过对有向图起点和终点的选取以及对关联矩阵采取去除与悬挂点和悬挂边相关联的行列后，就得到简化后的基于运输路线有向图的关联矩阵，其数据量相对其它算法构建的无向完全图已经大幅度减少。通过这种方法可以减少在后期算法中的运算量，降低算法的时间和空间复杂度。

3 双向搜索算法

3.1 算法定义

设简化后的有向图G=＜V，E＞，其中V={v1，v2，…，vn}为顶点集，n为简化后的顶点个数，E={e1，e2，…，em}为边集，m为简化后边的条数。

定义1：以v1作为起点，遍历其作为出度点的边，再以得到的边集查找对应的入度点，这样就输出一个路径集L1={v1v2，v1v3，…}，然后以路径集中各路径的终点为起点重复以上步骤，并在查找过程中删除有重复点的路径，得到路径集L2={v1v2v3，v1v3v2，…}，重复以上步骤集L={L1，L2，…，LA}。称以上这种查找为基于有向图的正向搜索，简称正向搜索。

定义2：以vn作为起点，遍历其作为入度点的边，再以得到的边集遍历对应的出度点，这样就输出一个路径集R1={vnvn—1，vnvn—2，…}，然后以路径集中各路径的终点为起点重复以上步骤，并在查找过程中删除有重复点的路径，得到路径集R2={vnvn—1vn—2，vnvn—2vn—1，…}，重复以上步骤得到路径合集R={R1，R2，…，RB}。称以上这种查找为基于有向图的逆向搜索，简称逆向搜索。

定义3：使用正向搜索和逆向搜索同时对有向图G=＜V，E＞进行的搜索称为基于有向图的双向搜索，简称双向搜索。

引理：对有向图G=＜V，E＞进行的双向搜索可全遍历顶点集V={v1，v2，…，vn}和边集E={e1，e2，…，em}。

这是显而易见的。

定理1：对有向图G=＜V，E＞进行双向搜索，存在vi∈L且vi∈R，使得L中的一条路径li={v1…vi}和R中的一条路径ri={vn…vi}组成的通路l为v1到vn的最短路径。

证明：设l为v1到vn的最短路径

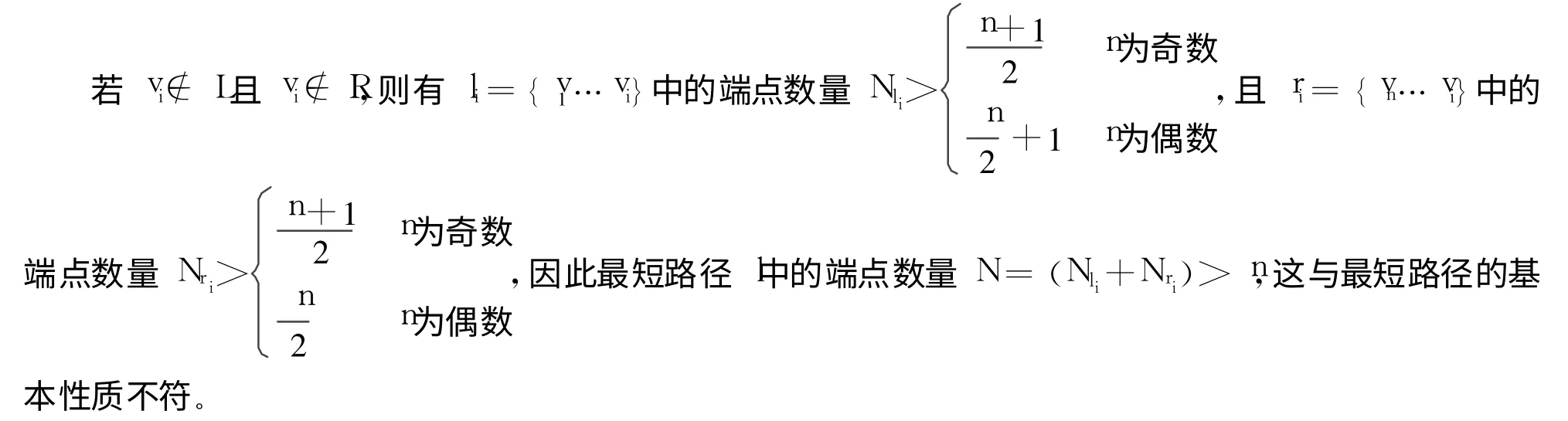
若vi∉L且vi∈R，由引理可知必存在vj使得lj={v1…vj}⊂li且ri⊂rj={vn…vj}，则有vj∈L且vj∈R，使得lj={v1…vj}和rj={vn…vj}组成的通路l为v1到vn的最短路径。

同理可证vi∈L且vi∉R情况。则定理证毕。

3.2 算法思想

根据两个端点分别循环使用正向搜索和逆向搜索，得到路径合集L={L1，L2，…，LA}和R={R1，R2，…，RB}，对其进行化简，将L中终点相同的路径进行比较，选出长度最短的，这样组成化简后的路径合集Lmin={v1…v2，v1…v3，…}，同理对R进行化简后得到新的路径合集Rmin={vn…vn—1，vn…vn—2，…}。

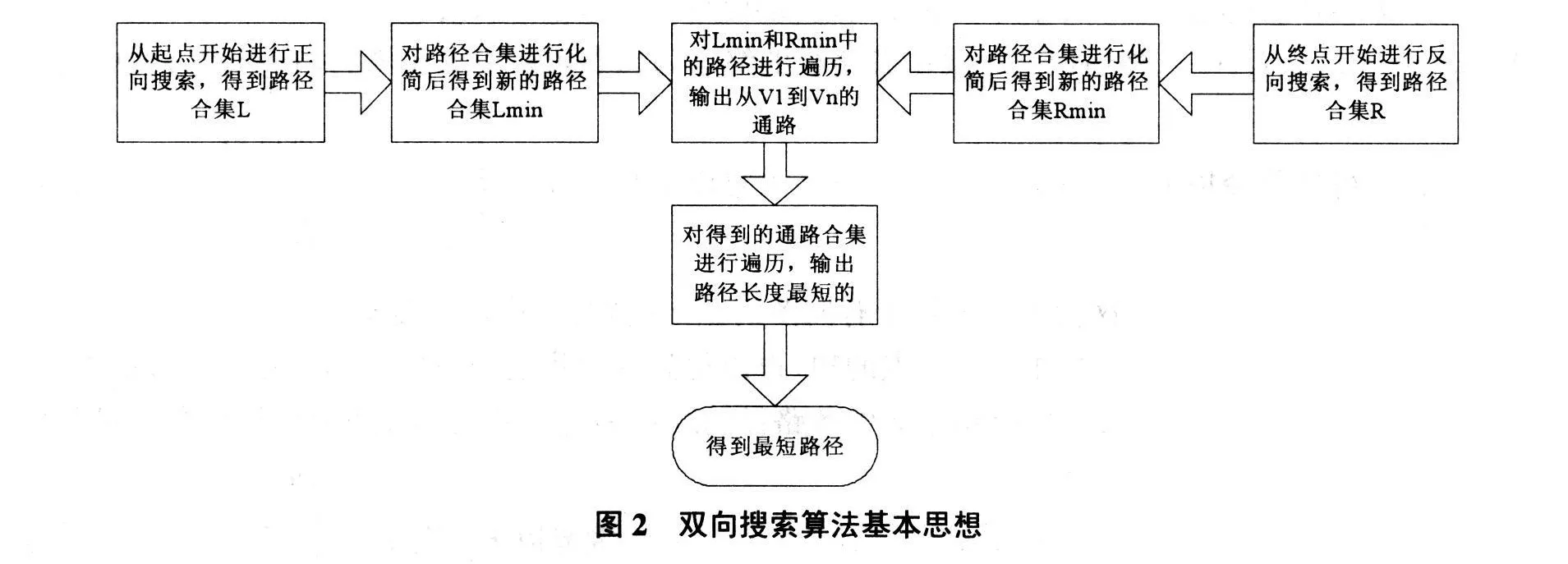
在Lmin和Rmin中搜索终点重合的路径组成一条由v1到vn的通路：s1=v1e1…en—1vn，当遍历完Lmin和Rmin中所有重合的路径后，会得到一个由v1到vn通路的集合S，设其有m项，则有：S={s1，s2，…，sm}，那么需要的最短路径即为min（S）所对应的路径。通过这样的方式，就可以将起点和终点之间的最短路径求出。其基本的思路也可以用图2来表示。