林宇敏

通过问题进行教学是数学教学活动最有效的方法.数学教学过程中,教师创设问题情境是为了激发学生积极主动地思考.那么,如何根据不同的教学内容提出问题,创设问题情境呢?以下是笔者在几何教学过程创设问题情境的一些尝试.

一、提供感性材料,创设问题情境

这是在概念教学中采用的一种方法.当学生的数学认知结构中具备一些理解新概念所必须的具体知识,其数量贫乏而且抽象程度较低时,他们只能从一定的具体例子出发,从他们实际经验的概念的肯定例证中,以归纳的方式抽取出一类事物的共同属性,从而获得概念,这时教师要为学生提供具有典型意义的、数量丰富的直观背景材料.这里强调背景材料的典型性是指所选事例应能够充分显示概念的本质属性,这样才能引导学生通过观察、辨别、抽象、概括,从中分析出共同属性,得到新概念.初中平面几何的入门教学,就经常采用这种方法.

例如,“平行线”概念的教学,在学生的数学认知结构中,已具备的是直线的有关概念(直线没有粗细、两边可以无限延伸等)、日常生活所接触到的有关事物(如铁轨、黑板的上下边沿、在笔直的公路上行驶的汽车的两道轮印等),这些是学生学习“平行线”概念的基础.为了使学生从这些具体事例中抽象概括出平行线的本质属性,教师可以这样来创设问题情境:首先给出学生熟悉的实际例子,提供平行线的形象:铁路上两条笔直的铁轨、直驶汽车的两道轮印、黑板的上下边缘等,并提问学生它们有哪些共同的属性.为了克服具体实例的局限性,可辅之以下说明:这里,我们把铁轨、车轮印、黑板边缘等都看成直线,这样就把学生的注意引向了观察两直线之间的关系,而不会过多地受具体材料的限制.通过观察、分析,学生可能会说出下列一些共同属性:它们都是两条直线,都可以向两边无限延伸,都在同一平面内,两条直线处处都隔得一样远,总不相交,等等.得出这些共同属性时,学生的思维中已经进行了初步概括,接着再提出下面的问题,以引起进一步的概括:“如何用几何语言将这些共同属性表达出来?”学生经过思考,会提出“在同一平面内两条直线不相交”“在同一平面内,两条直线之间的距离处处相等”.当学生的思维经历了以上两个过程后,已经获得对“平行线”的较全面的认识,但在概念的表达上还不够简练、精确,这时,教师可先指出:“有这种关系的两条直线叫做平行线.”然后提出:“如何准确简练地表达出平行线这一概念?”这一问题会引导学生进行一次抽象水平更高的概括,通过比较用几何语言表述的共同属性,在直观上理解了“不相交”与“处处相等”的等价性.最后教师给出平行线的定义:“同一平面内的两条不相交的直线叫做平行线.”这就完成了对“平行线”概念认识的全过程.

二、通过具体实验,创设问题情境

当学生的数学认知结构已经具备学习某一新数学知识的有关知识,但这一新知识与旧知识在逻辑联系的必然性上不太容易被学生感觉到时,教师可以通过有目的地为学生提供一些研究素材来创设情境,让学生自己进行实验、思考,通过运算、实践以及观察、分析、类比、归纳、作图等,探索规律、建立猜想、获得命题,在此基础上再进行逻辑上的论证,从而得到定理、法则或公式,等等.

例如,教学“三角形内角和定理”这节课时,就可以采用实验操作的办法来创设问题情境.在学生的数学认知结构中,已经有了角的有关概念,也有了三角形的概念,还具有同位角、内错角等有关平行线的性质.但对于“三角形的三个内角和为一定值180°”这一规律,学生可能意识不到这一命题与以上的有关概念之间的存在着逻辑联系,在这种情况下,教师可以这样来创设问题情境:首先可以提出问题:“请同学们画一些三角形(包括锐角三角形、直角三角形、钝角三角形),再用量角器量出三个角,计算一下,每一个三角形的三个角有什么联系?”学生会较快得出三个角的和在180°左右.这时,教师再进一步引导:“由于实验操作时有误差,在量每一个角时会有分秒之差,但和数都在180°左右,那么三角形的三个内角和是否为180°呢?请同学们把三个角拼在一起,观察一下,构成了一个怎样的角?”学生会根据老师的要求,饶有兴趣地进行拼接角的操作,最后发现,三个内角拼在一起构成一个平角,结合量角器测量的结果,学生自然猜想:“三角形的三个内角和为180°.”接着教师再提出:测量,剪拼角都可能出现一定的误差,而且实验的次数有限,要使猜想对一般的三角形都成立,必须进行严格的逻辑证明.那么,如何证明猜想呢?教师接下去可引导学生观察拼接时的图形,可凭借拼接时得到的感性经验,找到证明的方法:

如图1,把∠A、∠B剪下来与∠C拼在一起,组成了一个平角,E移到了BC的延长线E′处,D移到了D′,由于∠B=∠D′CE′,有平行线的判定定理可得D′C∥AB,这里,D′C∥AB的逻辑意义在“三角形的内角和为180°”成立的前提下得到的,虽然它是尚待证明的,但为证明指明了方向.由此学生可很容易地得到定理的证明:如图2,延长BC到E,过C在BA方向上作CD∥AB,则∠DCE=∠B,∠DCA=∠A,但∠BCA+∠ACD+∠DCE=180°,故有∠A+∠B+∠C=180°.

显然,如果没有实验操作,对于刚学平面几何不久的学生,要得到定理的证明(特别是添辅助线)是不容易的.

三、从具体问题的解决过程中,创设问题情境

学生在解决具体问题时,有时出现下面的情况:一是如果不学习新知识,则问题将无法解决;二是解决了问题后,要他说明解题过程的正确性时,不用新知识便无法说明理由,这样的情况都可引发问题情境.例如对于“等腰三角形的判定”这节课我是这样做的:

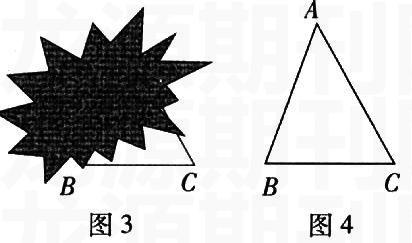
学生在学习“等腰三角形的判定”之前,已经具备了等腰三角形的概念、性质、等腰三角形的判定等知识,教师根据“性质定理”与“判定定理”的内在联系,让学生回忆定理后,提出了一个实际问题(问题根据需要自己编拟,以生动活泼、激发认知冲突为目的):“如图3,△ABC是等腰三角形,AB=AC,若一不小心,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C,大家想一想,能否把原来的△ABC重新画出来?”当学生经过动手实践,画出图形后,要学生说出画法:有的是用量角器量出∠C的度数,再以BC为一边,B点为顶点作∠B=∠C, ∠B与∠C的边相交得到顶点A;也有的是取BC边的中点D,过D作BC边的垂线,与∠C的一边相交得到点A,连AB.这些画法的正确性是需要用“判定定理”来判定的,而这正是要学的知识,于是教师用问题:“这样画出来的三角形是等腰三角形吗?”引出课题,创设了问题情境,教师再进一步引导学生分析画法的实质,并用几何语言概括出这个实质——有两个角相等的三角形是不是等腰三角形?再具体化,就是已知△ABC中,∠B=∠C,求证AB=AC.

这样,就由学生自己从问题出发获得了判定定理,接下来的问题自然地就引向了“如何证明”.通过启发,学生自己找到了多种证明方法:作顶角的平分线或底边的高,把△ABC一分为二,证明三角形全等可得到AB=AC,等等.在获得定理的证明以后,教师再要求学生“用正确的语言叙述这条判定定理”,使学生的思维再经历一次更高层次的概括,在纠正了“有两个底角相等的三角形是等腰三角形”的不妥之后,获得了准确的“判定定理”.

责任编辑 罗 峰