钱卫江

几何证明可培养学生的发散思维能力，在初中几何教学中是一个难点.为提高几何的解题能力需要让学生学会联想与推广.学习几何离不开解题，但要学好几何离不开归纳、总结.学生要善于归纳总结，题目解完了要勤于联想，这样才能真正学好几何.下面结合实例，说明归纳、总结、联想、推广的方法.

例如图1，从圆外一点P作切线PA，点B是PA上的中点，过点B作圆的割线BCD，连接PD交圆于点F，连接PC并延长，交圆于点E，求证：EF//PA．

分析：证明与圆有关的两直线平行的问题，应先考虑是否存在内错角、同位角相等，这是因为圆和三角形结合的图形中，一般可通过弧、弦找到不少角之间的关系.由于题中相切与图中线段直接相关，所以应联想到用“线”成比例去证明角相等.

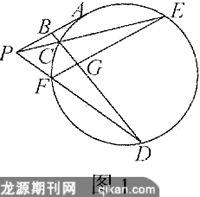
证明：∵PA切圆于A，点B为AP的中点，

∴AB２=BC·BD，AB=BP．

∴BP２=BC·BD，即BC/BP=BP/BD．又∠BPD=∠PBC，

∴△BPC∽△BDP． ∴ ∠D=∠BPC．

∵∠D=∠E， ∴ ∠BPC=∠E． ∴ EF//PA.

数学大师波利亚有一句名言:“掌握数学就是意味着善于解题.”善于解题关键要懂得解题后的反思，这个题目解完后有下列问题可供我们反思.

（1）实际上，由BP２=BC·BD，通过这个形式很容易联想得到PB与△PCD的外接圆相切，切点是P．由弦切角定理得，∠D=∠BPC．又因∠D=∠E，所以∠BPC=∠E．故EF//PA.这个证明方法更简捷，但对条件的处理和认识更深刻.

（2）据结果EF//PA，由夹在两平行线间的弧相等可知，A点是弧FAE的中点.

（3）在图中找与△PCB相似的三角形.通过相似可得很多相关的线段关系.

（4）尝试对于一个命题的条件和结论互换是否仍然成立.若PA//EF，B是PA的中点吗？根据上面的证明不难推出这个结论是成立的，于是引申出下列问题．

问题1如图1，从圆外一点作切线PA，点B在PA上，过点B作圆的割线BCD，连接PD交圆于点F，连接PC并延长，交圆于点E，若EF//PA ，求证：PB=BA．

证明：∵PA切圆于A，点B为AP上的一点，

∴AB２=BC·BD． ∵ EF//PA， ∴ △BPC∽△BDP．

∴BP ２=BC·BD． ∴ PB=BA．

问题2 原题中过B点作割线BCD一定要按照如图1吗？这条割线是否可任意作呢？

回答是肯定的.那么就可引出下面几种不同情形：如图2、图3．此时对原命题PA//EF同样成立（请读者自己完成）.

进行了上面的反思后，我们再作些联想和推广：将本例的题设作一些变更，可引出一些新的问题.

问题3 若将原题中的PB改成向圆外任意方向引线段时，可有如下命题：

如图４，从圆外一点P作切线PA和割线PCE，又从点P向任意方向作线段PB，使PB=PA，连接CB、EB，分别交圆于点F、D.求证：FD//PB．

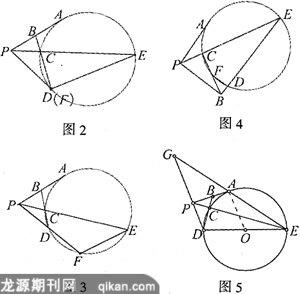
分析：与原题类似可证得△CPB∽△BPE，所以∠E=∠PBC．于是只需证明∠DFB=∠PBC，那么首先得证明∠E=∠DFB．（由C、F、D、E四点共圆即可得）

问题4若把问题1中PA切线去掉，把原来的一些条件加强，可得到如下命题：如图5，已知DE为⊙O的直径，A为⊙O上一点，延长EA至G，使AG=AE，AP⊥CD，垂足为P，PE交⊙O于C，CD交AP于B.求证:PB=BA.

分析：要证PB=BA，直接“线”相等的等量关系没有，所以要找中间量转化．由条件AP⊥CD，DE为直径，可由射影定理得BP２=BC·BD，容易联想到要证AB为切线，因此该命题实际就可转化为问题1的证明了.

证明：连接OA．

∵AB是⊙O的直径， ∴ CE⊥BD．

又∵AP⊥CD，由射影定理得：BP２=BC·BD．

∵A，O分别为GE，DE的中点， ∴ AO为为△GDE的中位线．

∴AO∥GD．∴ AO⊥AP．可知AP为⊙O切线.

则AB２=BC·BD．∴ AB２=BP２，即PB=BA．

小结：通过解题后的反思、联想，把与之有关的知识、方法、技巧都联系起来，可扩大和加强数学知识的网络，收到举一反三的效果.通过拓展、推广，从已知走向未知，进一步发现的往往是新的方法和技巧.希望读者学习此例题后，能在以后几何的学习中得到更多的收获.